
Читайте также:
|
Закономерности естественного искривления скважин выявляются на основании фактических замеров искривления по группе скважин. Замеры зенитных и азимутальных углов по скважинам 1, 2, 3, 4 приведены в табл. 1.
Таблица 1
Замеры зенитных и азимутальных углов
| Глубина,м | Скв.1 | Скв.2 | Скв. 3 | Скв. 4 | ||||
| θ | α | Θ | α | θ | α | θ | α | |
| 17 20 | 15 20 | 16 00 | 18 00 | |||||
| 16 30 | 15 00 | 16 10 | 18 00 | |||||
| 17 00 | 14 00 | 15 20 | 16 10 | |||||
| 16 00 | 13 00 | 14 00 | 15 10 | |||||
| 15 00 | 13 10 | 13 30 | 14 10 | |||||
| 14 30 | 13 20 | 12 00 | 14 00 | |||||
| 14 00 | 12 00 | 12 10 | 14 00 | |||||
| 14 20 | 12 10 | 12 00 | 13 10 | |||||
| 13 00 | 11 20 | 11 00 | 13 00 | |||||
| 12 00 | 11 40 | 10 40 | 12 30 | |||||
| 12 10 | 10 10 | 9 40 | 12 00 | |||||
| 11 10 | 9 30 | 8 30 | 12 10 | |||||
| 10 20 | 8 30 | 7 30 | 11 00 |
На основании данных табл. 1 будет проведён корреляционный анализ зависимостей зенитного и азимутального (отдельно) углов от длины скважины и оценена степень связи внутри названных зависимостей с помощью коэффициента корреляции.
Данные для проведения корреляционного анализа связи величины зенитного угла с длиной скважины заносятся в табл. 2.
В столбце li записываются средние значения глубин стометровых отрезков скважин.
В столбце θi записываются средние значения зенитных углов по всем четырем скважинам для соответствующих интервалов глубин.
Таблица 2
Данные для проведения корреляционного анализа связи величины зенитного угла с длиной скважины
| li, м | θi, град | li – 
| θi – 
| (li –  )2 )2
| (θi –  )2 )2
| (li –  ) ∙ (θi – ) ∙ (θi –  ) )
|
| 16,3 | - 250 | 3,17 | 10,05 | -792,5 | ||
| 14,5 | - 150 | 1,37 | 1,88 | -205,5 | ||
| 13,4 | - 50 | 0,27 | 0,07 | -13,5 | ||
| 12,9 | -0,23 | 0,05 | -11,5 | |||
| 11,5 | -1,63 | 2,66 | -244,5 | |||
| 10,2 | -2,93 | 8,58 | -732,5 | |||
| 78,8 | 23,3 | -2000 |
Остальные столбцы рассчитываются в соответствии с приведенными в заголовке таблицы формулами.
 (1)
(1)
где  – среднее значение глубины по всей выборке; n – число строк в таблице.
– среднее значение глубины по всей выборке; n – число строк в таблице.
 (2)
(2)
где  – среднее значение зенитного угла по всей выборке.
– среднее значение зенитного угла по всей выборке.
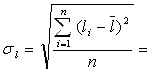
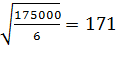 м, (3)
м, (3)
где 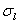 – среднеквадратическое отклонение глубины скважины.
– среднеквадратическое отклонение глубины скважины.

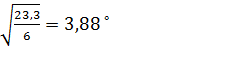 (4)
(4)
где  – среднеквадратическое отклонение зенитного угла.
– среднеквадратическое отклонение зенитного угла.
Оценка степени связи зенитного угла скважины с её глубиной осуществляется с помощью коэффициента корреляции  :
:
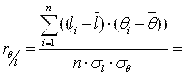
 (5)
(5)
Искомое корреляционное уравнение зависимости зенитного угла от глубины скважины определяется как:

 (6)
(6)
На основании проведенных расчётов построены эмпирический (по данным столбцов li и θi табл. 2) и теоретический (по корреляционному уравнению) графики зависимости зенитного угла от глубины скважины (рис.1).

Рисунок 1 - Зависимость зенитного угла (θ) от глубины скважины (l):
1 – эмпирическая; 2 – теоретическая
Аналогичным образом проводится корреляционный анализ зависимости азимутального угла от глубины скважины.
Таблица 3
Данные для проведения корреляционного анализа связи величины азимутального угла с длиной скважины
| li, м | αi, град | li – 
| αi – 
| (li –  )2 )2
| (αi –  )2 )2
| (li –  ) ∙ (αi – ) ∙ (αi –  ) )
|
| 102,5 | - 250 | 5,2 | 27,04 | -1300 | ||
| 99,3 | - 150 | -300 | ||||
| 97,8 | - 50 | 0,5 | 0,25 | -25 | ||
| 96,5 | -0,8 | 0,64 | -40 | |||
| 94,8 | -2,5 | 6,25 | -375 | |||
| -4,3 | 18,49 | -1075 | ||||
| 583,9 | 56,67 | -3115 |
В столбце li записываются средние значения глубин стометровых отрезков скважин.
В столбце αi записываются средние значения азимутальных углов по всем пяти скважинам для соответствующих интервалов глубин.
Остальные столбцы рассчитываются в соответствии с приведенными в заголовке таблицы формулами.
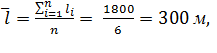 (7)
(7)
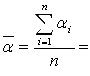 где
где  – среднее значение глубины по всей выборке; n – число строк в таблице.
– среднее значение глубины по всей выборке; n – число строк в таблице.
 ˚ (8)
˚ (8)
где  – среднее значение азимутального угла по всей выборке.
– среднее значение азимутального угла по всей выборке.

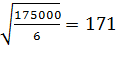 м, (9)
м, (9)
где 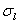 – среднеквадратическое отклонение глубины скважины.
– среднеквадратическое отклонение глубины скважины.

 (10)
(10)
где  – среднеквадратическое отклонение азимутального угла.
– среднеквадратическое отклонение азимутального угла.
Оценка степени связи азимутального угла скважины с её глубиной осуществляется с помощью коэффициента корреляции  :
:

 (11)
(11)
Искомое корреляционное уравнение зависимости зенитного угла от глубины скважины определяется как:

 (12)
(12)
На основании проведенных расчётов построены эмпирический (по данным столбцов li и αi табл. 3) и теоретический (по корреляционному уравнению) графики зависимости азимутального угла от глубины скважины (рис. 2).

Рисунок 2 - Зависимость азимутального угла (α) от глубины скважины (l):
1 – эмпирическая; 2 – теоретическая
Дата добавления: 2015-08-10; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Введение | | | Выбор средств и описание технологии борьбы с естественным искривлением |