Проверочный расчет оси траверсы крюковой подвески.

Максимальный изгибающий момент в сечении А-А (рис.12):

М_А-А = Q ∙ g ∙ l_т / 4

l_т – расчетная длина траверсы для 2-х блочной подвески, l_т = 88 мм.

М_А-А = 2500 ∙ 9,81 ∙ 0,088 / 4 =539 Н·м

Максимальный изгибающий момент в сечении B-B:

М_B-B = (Q · g · l₂) / 4

l₂ – длина средней части траверсы;

b_тр ≈ D_пдш +10=68+10=78 мм– ширина траверсы;

Принимаем b_тр=80 мм;

D_пдш – внешний диаметр упорного подшипника;

l₂= (l_т – b_тр+δ)/2= (l_т – b_тр + δ)/2= (88—80+8)/2=8 мм

М_B-B = (2500 ∙ 9,81· 0,008) / 4 = 196 Н·м

Условие прочности при изгибе:

где М – изгибающий момент в рассматриваемом сечении;

W – момент сопротивления сечения;

[σ]_и – допускаемое напряжение при изгибе;

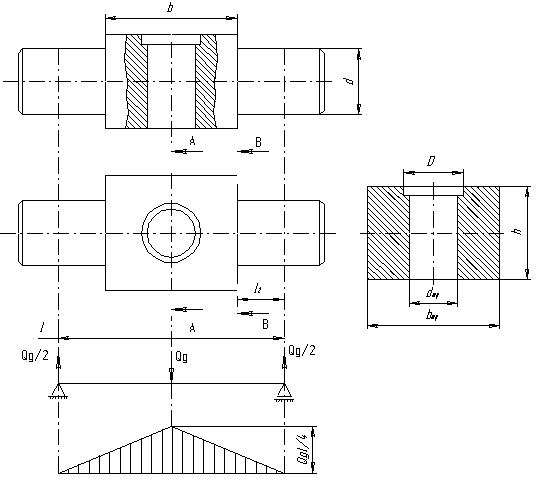
Рисунок 12 - Расчет траверсы крюковой подвески

где σ_-1 = 250 (МПа) – предел выносливости для стали 45.

k`₀ = 2 – коэффициент, учитывающий конструкцию детали.

[ n ]= 1,7 –допустимый коэффициент запаса прочности.

[σ]_и = (МПа)

Момент сопротивления сечения А-А:

где d_кр – диаметр отверстия для крюка;

h – высота сечения

Преобразуем:

6 · М_А-А = h² (b_тр – d_тр) · [σ]_и

Отсюда:

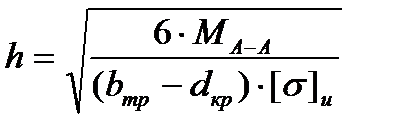
м

Т.е. h ≥ 10,6 мм, принимаем h = 30 мм

Момент сопротивления сечения В-В:

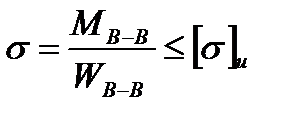
W_B-B ≥ М_В-В / [σ]_и = 196 / (102,94·10⁶)= 1,9 · 10^-6 м³

W_B-B = π · d³ / 32 ≈ 0,1d³

Получаем равенство:

0,1d³ ≥ 1,9 · 10^-6

d ≥ м

Принимаем d = 30 мм

на смятие:

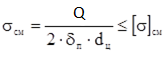
где Q - грузоподъемная сила, Н;

δ_n - толщина планки, мм;

d_ц - диаметр цапфы траверсы, мм;

[σ]_см - допускаемое напряжение смятия, [σ]_см = 80…150 МПа,

.

Дата добавления: 2015-08-10