Показники варіації.

Завдання 2. За даними індивідуальних завдань обчислити показники варіації зважені (розмах варіації, середнє лінійне відхилення, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації). Зробити висновки.

Таблиця... Вихідні та розрахункові дані для обчислення показників варіації зважених

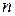
Урожайність зернових культур, ц	Кількість господарств,	Розрахункові величини
середина інтервалу
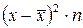
20,5 – 22,5		21,5	3,1	12,4	9,61	38,44
22,5 – 24,5		23,5	1,1	5,5	1,21	6,05
24,5 – 26,5		25,5	0,9	6,3	0,81	5,67
26,5 – 28,5		27,5	2,9	11,6	8,41	33,64
Разом		х	х	35,8	х	83,80

Розмах варіації – це різниця між найбільшим і найменшим значенням варіюючої ознаки:

.

Середнє лінійне відхилення – дорівнює середній з абсолютних відхилень усіх значень варіюючої ознаки від її середнього значення.

.

Дисперсією – називається середній квадрат відхилень усіх значень варіюючої ознаки від її середньої арифметичної.

.

Середнє квадратичне відхилення визначають як корінь квадратний з дисперсії:

.

Середнє квадратичне відхилення характеризує середнє коливання ознаки в сукупності, викликане індивідуальними особливостями сукупності. Воно вимірюється тими самими одиницями, що й варіанти досліджуваної ознаки.

Для того, щоб співставити сукупності з різними значеннями середньої арифметичної та середнього квадратичного відхилення, визначають коефіцієнт (процент) варіації.

Коефіцієнтом варіації називають відношення середнього квадратичного відхилення до середнього значення варіюючої ознаки. Коефіцієнт варіації застосовують для порівняння варіації різних явищ. Коефіцієнт варіації визначається так:

.

.

.

.

,

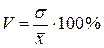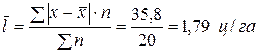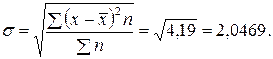
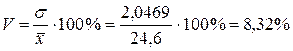Сукупність можна вважати однорідною, оскільки

Дата добавления: 2015-08-10