Середні величини

Тема. Аналіз рядів розподілу

Завдання 1. За даними індивідуальних завдань обчислити середню урожайність зернових культур звичайним способом та способом моментів, моду, медіану.

Таблиця. Ряд розподілу господарств за урожайністю зернових культур

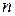
Урожайність зернових культур, ц	Кількість господарств,	Розрахункові величини
сума нагромаджених частот	середина інтервалу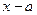
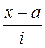
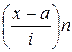
20,5 – 22,5			21,5	-4	-2	-8
22,5 – 24,5			23,5	-2	-1	-5
24,5 – 26,5			25,5
26,5 – 28,5			27,5
Разом		х	х	х	х	-9

Середню урожайність зернових обчислюємо за допомогою середньої арифметичної зваженої:

.

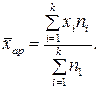
Середню урожайність зернових можна обчислити середньою за способом моментів. При розрахунку середньої арифметичної способом моментів за початок відліку взято усереднену варіанту з найбільшою частотою 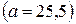, величина інтервалу .

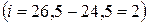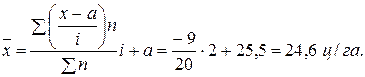
Модою називають значення ознаки, яке найчастіше повторюється в досліджуваній сукупності.

У дискретному варіаційному ряді мода визначається без ніяких розрахунків. Потрібно вибрати найбільшу частоту і варіанта, яка їй відповідає і буде модою. Наприклад, трактористи бригади за змінним виробітком поділяються на такі групи:

Виробіток тракториста за зміну, га
Кількість трактористів

Варіююча ознака – виробіток, а частота кількість трактористів. Модою або модальною середньою в даному прикладі буде змінний виробіток 7 га, оскільки йому відповідає найбільша частота (15).

Дещо складніше визначають моду в інтервальному ряду. Спочатку визначають модальний інтервал, тобто інтервал, який має найбільшу частоту. Потім модальне значення ознаки визначають за формулою:

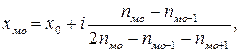
де 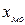– мода; 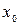– нижня межа модального інтервалу, 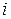– величина модального інтервалу; 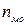– частота модального інтервалу; 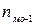– частота інтервалу, що передує модальному; 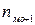– частота інтервалу, що слідує за модальним.

Обчислення моди для інтервального ряду розглянемо за даними таблиці.

У цьому прикладі найбільшою є кількість господарств, де урожайність зернових знаходиться в межах від 24,5 до 26,5. Цей інтервал і буде модальним.

Підставивши дані у формулу для обчислення моди, дістанемо:

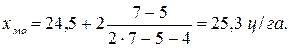
Отже, в даній сукупності господарств найчастіше зустрічаються господарства з урожайністю зернових 25,3 ц/га.

За цією формулою можна обчислювати модальну середню лише при умові, що інтервали рівні. Якщо ж інтервали нерівні, ряд спочатку треба перебудувати, а потім обчислювати моду.

Медіаною називають значення варіюючої ознаки, що міститься всередині ранжированого ряду розподілу. Медіана є центром розподілу сукупності і ділить її на дві рівні за кількістю частини.

Якщо кількість членів ряду непарна, то медіаною буде центральне значення варіюючої ознаки.

Наприклад, перед постановкою на відгодівлю були зважені 7 поросят, які мали вагу, кг: 35, 37, 38, 39, 40, 42, 44. Медіана цих значень буде знаходитись на 4 місці і дорівнюватиме 39 кг.

Якщо ж розглядається ряд з парним числом варіант, то медіана знаходиться як середня арифметична з двох центральних варіант. Наприклад, від кожної з 10 корів було надоєно таку кількість молока, кг: 8, 9, 10, 12, 13, 15, 17, 18, 20, 21. Місце медіани знайдемо так: до обсягу ряду додамо одиницю і одержаний результат поділимо на 2, тобто .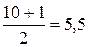

Отже, медіана знаходиться між 5 і 6 варіантою, тобто між 13 і 15 і дорівнює 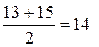кг.

Для обчислення медіани в інтервальному варіаційному ряду спочатку знаходять медіанний інтервал, в якому знаходиться значення ознаки, що ділить ряд розподілу пополам. Його визначають нагромадженням частот. Починаючи з першої, поки не одержиться сума, що перевищує півсуму частот. Медіану обчислюють за формулою:

,

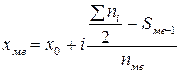де 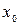– нижня межа медіанного інтервалу; 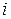– величина медіанного інтервалу; 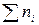– сума частот ряду розподілу; 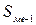– сума нагромаджених частот перед медіанним інтервалом; 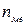– частота медіанного інтервалу.

Обчислимо медіану за даними табл. Половина суми частот дорівнює 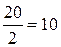, а сума, що її перевищує 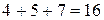, отже, медіаною буде значення варіанти з урожайністю зернових від 24,5 до 26,5. Звідси 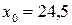; ; 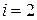; 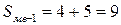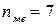. Підставивши ці значення у формулу медіани, одержимо:

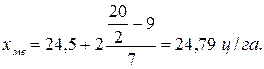
Отже, половина всіх господарств має урожайність зернових не менше як 24,79 ц/га, а решта – більше як 24,79 ц/га.

Дата добавления: 2015-08-10