Основные методы кинематического анализа.

Задачей кинематического анализа является изучение движения звеньев механизма вне зависимости от сил, действующих на них.

В результате по заданному закону движения ведущего звена определяются положения, угловые скорости и ускорения ведомых звеньев, а также перемещения, скорости, ускорения отдельных точек.

Кинематическое исследование схем механизмов производится аналитическими и графическими методами.

Аналитические методы позволяют с требуемой точностью установить аналитически функциональную зависимость кинематических параметров механизма от параметров звеньев. Эти методы отличаются сложностью и трудоемкостью. Их применение оправдывается при использовании ЭВМ. Графические методы исследования разделяются на:

1. Метод построения кинематических диаграмм.

2. Метод планов скоростей и ускорений. Метод построения кинематических диаграмм основан на графическом изображении перемещений, скоростей или ускорений отдельных точек звеньев в функции времени или перемещений ведущего звена.

Переход от графиков перемещений к графикам скоростей и ускорений производится путем графического дифференцирования, а обратно - графическим интегрированием.

Этот метод дает наглядное представление об изменении кинематических параметров во времени.

Метод планов скоростей и ускорений позволяет при наличии планов положений механизма определить скорости и ускорения любых точек механизма для любого момента времени.Кинематические исследования этим методом начинаются с построена плана механизма, т. е. изображение его кинематической схемы в выбранном масштабе длины звеньев

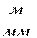[ ],где -истинный размер звена, 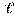-его масштабное изображение в мм.

Графоаналитический метод кинематического анализа - метод планов скоростей и ускорений.

Пусть дан кривошипно - ползунный механизм, схема которого пока­зана на рис. 2.7. Известны длины звеньев, положение механизма и постоянная угловая скорость кривошипа W₁. Требуется определить скорости и ускорения точек А, В, С, и угловые скорость и ускоре­ние шатуна W₂ и E₂.

2.3.1 Построение планов скоростей. Определяем скорость точки А кривошипа по формуле 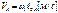,Здесь - длина кривошипа ОА в М.

Назначаем полюс плана скоростей Р_V и из него перпендику­лярно кривошипу ОА откладываем отрезок P _V a (рис2.8), представляющий собой вектор скорости точки А при масштабном коэффициенте плана скоростей . который определяется выражением

где P _V a -длина вектора в мм на плане скоростей. Для определения скорости точки В движение шатуна разложим на переносное поступательное со скоростью точки А и относитель­ное вращательное вокруг этой точки. Такое разложение движения описывается векторным уравнением.

В таблицу под уравнением внесены данные о величине и нап­равлении векторов. Неизвестными здесь являются величины векторов.

V_B и V_BA при известных их направлениях. Такое уравнение может быть решено графически построением плана скоростей. Из полюса P_V проводится направление вектора , а из конца вектора скорости точки А - направление вектора . На пересечении этих прямых находится конец вектора скорости точки В (точка "в" плана скоростей). Теперь можно найти скорость любой другой точки. Например, для скорости точки С можно записать два векторных уравнения:

,

Проведя из точек а и в плана скоростей прямые, перпендикулярные отрезки АВ и ВС шатуна найдем конец вектора скорости точки С, начало его лежит в полюсе Р_V. Величины скоростей точек А, В, С в м/с определяются выражениями:

Таким образом, если у звена известны величина и направление скорости одной точки и направление скорости (траектория) другой точки, то можно определить скорость любой его точки.

Построение планов ускорений.

Определяем ускорение точки А кривошипа по формуле

Здесь , - нормальное и тангенциальная составляющие. В нашем примере , поэтому Нормальное ускорение определяется выражением 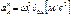Этот вектор направлен параллельно ОА к центру вращения кривошипа (от точки А к точке 0 на звене).Назначаем масштабный коэффициент плана ускорений и определяем длину вектора Р_aa который будет представлять ускорение точки А.

Из полюса плана ускорений P_a откладываем отрезок рис. 2.9. Здесь стрелка внизу показывает направление вектора от точки А к точке 0 на звене.Для определения ускорения точки В опять разложим движение шатуна, как при построении плана скоростей. Тогда будем иметь

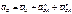В этом уравнени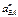и и -нормальная и тангенциаль­ная составляющие относительного ускорения . Нормальная состав­ляющая вычисляется по формуле

Здесь ab - отрезок плана скоростей. Начало и конец вектора 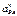на плане ускорений обозначим точками а и n₂; n -говорит, что отложено нормальное ускорение, индекс 2 - что рассматривалось звено 2. Полученное векторное уравнение может быть решено графически построением плана ускорений. Для этого из полюса Р_a проводим направление вектора абсолютного ускорения точки В параллельно направляющим ползуна b и далее строим векторную сумму по правой части уравнения. Пересечение известных по направлению векторов и ,и дает решение - точку "в" плана ускорений. Отрезок n₂b в принятом масштабе представляет вектор , величина которого равна Зная величину и направление тангенциальной составляющей отно­сительного ускорения точек В и А, можно определить величину и направление углового ускорения шатуна 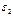. Его величина определяется выражением Для определения направления - вектор показываем выходящим из точки В на звене.

Свойства планов скоростей.

Началом векторов абсолютных скоростей является одна точка P_V - полюс плана скоростей. Вытекает из определения.

2. Отрезки, соединяющие концы векторов абсолютных скоростей, при принятом масштабном коэффициенте представляют относительные скорости точек.

3. Одноименные фигуры на звене и плане скоростей подобны, а одноименные отрезки пропорциональны и повернуты на 90° в сторону вращения звена.

4. Всем точкам, скорость которых равна 0, на плане скоростей отвечает одна точка-полюс P_V.

Свойства планов ускорений.

Эти свойства аналогичны свойствам планов скоростей и доказы­ваются аналогично.

1. Векторы абсолютных ускорений всех точек берут начало в одной точке - полюсе P_a. Вытекает из определения.

2. Отрезки соединяющие концы векторов абсолютных ускорений, при принятом масштабном коэффициенте и 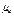представляют относительные ускорения точек. Например,

3. Одноименные фигуры на звене и плане ускорений подобны, а одноименные отрезки пропорциональны и повернуты в сторону углового ускорения звена на одинаковых угол 180°- .

4. Всем т очкам, ускорение которых равно нулю, на плане ускоре­ний соответствует одна точка - полюс Р_a.

17) Задачи динамического анализа машин и механизмов.При рассмотрении вопросов кинематического анализа механизмов мы всегда предполагаем движение входных звеньев заданным. Движение выходных звеньев изучается в зависимости от заданного движения входных. При этом силы, действующие на звенья механизма, и силы, возникающие при его движении, нами не изучаются. Таким образом, при кинематическом анализе исследование движения механизмов ведется с учетом только структуры механизмов и геометрических соотношений между размерами их звеньев. динамический анализ механизмов имеет своими задачами: а) изучение влияния внешних сил, сил веса звеньев, сил трения и массовых сил (сил инерции) на звенья механизма, на элементы звеньев, на кинематические пары и неподвижные опоры и установление способов уменьшения динамических нагрузок, возникающих при движении механизма; б) изучение режима движения механизма под действием заданных сил и установление способов, обеспечивающих заданные режимы движения механизма. Первая задача носит название силового анализа механизмов, а вторая задача — название динамики механизмов. В динамический анализ механизмов может быть включен и ряд других задач, имеющих важное техническое значение, а именно: теория колебаний в механизмах, задача о соударении звеньев механизмов и др. Но эти вопросы являются предметом изучения в специальных курсах, так как при решении их необходимо применять методы теории упругости, а в теории механизмов и машин задачи решаются обычно в предположении, что звенья механизмов являются абсолютно жесткими. Первая из указанных задач динамики механизмов имеет своей целью определение внешних неизвестных сил, действующих на звенья механизма, а также усилий (реакций), возникающих в кинематических парах при движении механизма. К внешним силам, например, относятся давление рабочей смеси (газа или жидкости) на поршень кривошипно-ползунного механизма двигателя внутреннего сгорания, парового двигателя, компрессора, вращающий момент, развиваемый электродвигателем на валу рабочего механизма, и др. Некоторые силы возникают в результате движения механизма. К этим силам, например, относятся силы трения при движении, силы сопротивления среды и т. д. Некоторые силы, как, например, динамические реакции в кинематических парах, возникают при движении вследствие инерции звеньев. Изучение природы СИЛ требует не только теоретического, но и экспериментального исследования. С помощью современных измерительных приборов можно весьма точно определять различные силы, действующие на отдельные звенья механизма, и выявлять их зависимости от различных факторов. Если известны внешние силы, действующие на звенья механизма, и известны законы движения всех его звеньев, то можно методами, излагаемыми в механике, определить силы трения и реакции связей в кинематических парах, силы сопротивления среды, силы инерции звеньев и другие силы, возникающие при движении механизма, и тем самым произвести так называемый силовой расчет механизма. К первой задаче динамического анализа механизмов относится также вопрос об устранении дополнительных динамических нагрузок от сил инерции на опоры механизма соответствующим подбором масс звеньев. Этот вопрос рассматривается в теории уравновешивания масс в механизмах. Вторая задача имеет своей целью определение мощности, не обходимой для воспроизведения заданного движения машины или механизма, я изучение законов распределения этой мощности на выполнение работ, связанных с действием различных сил на механизм, а также решение вопроса о сравнительной оценке механизмов с помощью коэффициента полезного действия, характеризующего степень использования общей энергии, потребляемой машиной или механизмом, на полезную работу. К этой же задаче относится вопрос об определении истинного движения механизма под действием приложенных к нему сил, т. е. задачи о режиме его движения, а также вопрос о подборе таких соотношений между силами, массами и размерами звеньев механизма или машины, при которых движение механизма или машины было бы наиболее близким к требуемому условию рабочего процесса. Эта задача обычно носит название теории движения машины или механизма под действием заданных сил

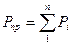18 Приведение сил и масс. Динамические модели машины.

Определение закона движения механизма через уравнение (3.39), в котором кинематические параметры звеньев находятся в определенных соотношения друг с другом, выражаемых через свои уравнения, довольно затруднительно. Для упращения составления уравнения движения механизма и его решения,достаточно, пользуясь методом приведения сил и масс, установить закон движения его звена или одной точки, т.е. найти только одну неизвестную функцию. Решение этой задачи осуществляется созданием динамической модели машины, в которой модель имеет такой же закон движения как и сама машина.

Для этой модели все силы и моменты сил, действующие на машину, заменяются одной силой или моментом сил называются приведенной силой или приведенной массой. Приведение сил и моментов сил осуществляются либо к точке (если обобщенной координатой является линейная координата), либо к звену (если обобщенной координатой является угловая координата). В качестве точки приведения обычно выбирается точка на ведущем звене, в качестве звена приведения – ведущее звено. Если ведущее звено механизма является кривошипом, то и звено при -ведения имеет такой же вид (кривошип), если ведущее звено – ползун, то звено приведения - ползун. Условим приведения сил и масс является закон сохранения энергии. Т.е. мощность или работа приведенной силы или момента сил должна равняться суммарной мощности или работе всех внешних сил или моментов сил, а кинетическая энергия звена приведения равна суммарной кинетической энергии всех звеньев.

Если приведенная сила F_пр, приложенная к точке направлена по касательной к её траектории,то равенство (3.41) можно записать как

Где, F_i, M_i - сила и момент, приложенные к звену; V_i - скорость точки приложения силы; w - угловая скорость звена.

Если вместо приведенной силы определяется приведенный момент сил,то аналогично равенству (3.43)

Из уравнений (3.43) и (3.44) получим Из условия (3.42) Где 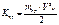для звена приведения - ползун; для звена приведения - кривошип.

Подставляя соответствующие выражения в формулу (3.47) и разрешая её относительно приведенных параметров получим: Как известно величины отношения скоростей (аналоги скоростей) зависят только от положения механизма, будучи одинаковыми при любом законе движения механизма. Поэтому и приведенная сила или приведенный момент сил, приведенная масса или приведенный момент инерции от закона движения не зависят, а зависят от положения его звена приведения.

Дата добавления: 2015-08-10