Механизмы плоские и пространственные. Число свободы механизма и его определение.

Плоский механизм- мех., в котором все точки и звенья перемещаются в плоскостях // между собой.

Пространственный мех.- мех., в котором все точки и звенья перемещаются в плоскостях не // между собой.

W число степеней свободы мех-ма. W=1 – для плоских мех-мов Wне= 1 – для пространственных мех-мов Определение числа степеней свободы мех-ма W=3*n-2*P5-P4- формула Чебышева для плоских мех-мов. W-число степеней свободы n-число подвижных звеньев Р5-число пар 5-го класса мех-ма Р4-число пар 4-го класса мех-ма Для плоских мех-мов если Wне= 1 то допущена ошибка, либо присутствуют звенья, создающие лишнюю степень свободы.

5. Структурный синтез механизмов на примере плоского механизма Осн. пр-п образования мех-ов был впервые сформулирован в 1914 г. Л. В. Ассуром. Им был продолжен и развит м-д образования мех-ов путем последовательного наслоения кинематических цепей, обладающих опред. структурными св-ми. Этот м-д легко проследить, рассматривая какой либо конкретный механизм, например:

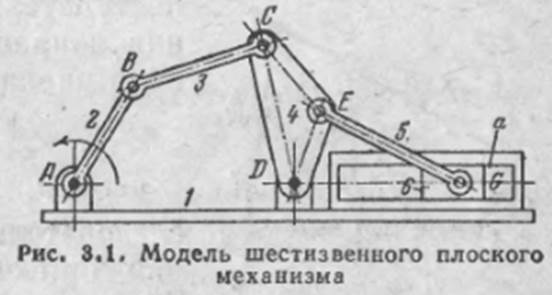
Этот мех-м имеет 5 подвижных звеньев, образующих семь кинематических пар 5 класса. Сл-но, по ф-ле Чебышева число его степеней свободы равно W=3*n-2*P5=3*5-2*7=1т. е. данный мех-м обладает одной степенью свободы. Выберем в качестве начального звено 2. Тогда мех-м будет состоять из нач. звена 2, обладающего одной степенью свободы, стойки 1 и звеньев, образующих кинематическую цепь, состоящую из звеньев 3, 4, 5 и 6. Процесс образования этого мех-ма можно представить как последовательное присоединение к начальному звену 2 и к стойке 1 кинематической цепи, состоящей из звеньев З и 4. Тогда получим четырехзвенный механизм АВCD, обладающий одной степенью свободы. Далее к звену 4 механизма AВСD и стойке 1 присоединим кинематическую цепь, состоящую из звена 5 и ползуна 6. Тогда получим 6-звенный мех-м, обладающий также одной степенью свободы. Нетрудно теперь установить определенную закономерность процесса образования мех-ма. В самом деле, любой мех-м имеет одно неподвижное звено (стойку). У данного мех-ма стойкой будет звено 1. далее, мех-м должен иметь число начальных звеньев, равное числу его степеней свободы. В нашем случае мех-м обладает одним начальным звеном 2, так как степень свободы мех-ма равна W=1. Т.к. после присоединения звеньев 3, 4, 5 и б число степеней свободы всего мех-ма осталось равным W=1, то, след-но, кинематическая цепь, состоящая из звеньев 3, 4, 5 и 6, присоединенных к нач. звену 2 и стойке 1, обладает нулевой степенью свободы относительно тех звеньев, к которым эта цепь присоединяется. При последовательном присоединении групп необходимо руководствоваться определенными правилами. При образовании мех-ма с одной степенью свободы 1-я группа присоединяется свободными эл-ми звеньев к нач. звену и к стойке. Последующие группы могут присоединиться к любым звеньям полученного мех-ма только так, чтобы звенья группы обладали подвижностью друг относительно друга.

6. Принцип образования механизмов, впервые сформулированный Л.В. Ассуром:

схема любого механизма может быть составлена последовательным присоединением к механизму I класса групп звеньев с нулевой степенью подвижности – групп Ассура.

Группа Ассура - незамкнутая кинематическая цепь с нулевой степенью подвижности. Сколько бы групп Ассура ни присоединяли к механизму I класса, степень подвижности механизма остаётся равной единице.

Для плоского механизма, состоящего только из кинематических пар 5-го класса, степень подвижности групп Ассура определится согласно формуле Чебышева

Поскольку n и p5 могут быть только целыми числами, из равенства следует, что в группах Ассура возможны след. сочетания количества звеньев и примыкающих к ним кинематических пар:

Практически встречаются только первые два сочетания

Разложение механизма на структурные группы необходимо для решения задач кинематического и динамического анализа, обеспечивая статическую определимость составляющих частей схем плоских механизмов.

Структурный анализ механизма следует проводить путём расчленения его на структурные группы в порядке, обратном образованию механизма.

Выделение групп Ассура начинают с наиболее удалённой группы (последней в порядке присоединения к механизму I класса). В результате отсоединения структурных групп остается механизм I класса.

Дата добавления: 2015-08-10