Курск 2010

Юго-западный государственный университет

Кафедра электроснабжения

Утверждаю

Зав. кафедрой Электроснабжения

_______________/ Сергеев С.А./

Сентября 2010г.

ЗАДАЧИ

К ЭКЗАМЕНАЦИОННЫМ БИЛЕТАМ ПО ДИСЦИПЛИНЕ

Quot; ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

(УПРАВЛЕНИЕ ТЕХНИЧЕСКИМИ СИСТЕМАМИ) "

Курск 2010

Задача 1. Линеаризовать уравнение характеристики элемента умножения y=x₁x₂ в точке y₀=x₀₁x₀₂.
Задача 2. Написать уравнения состояния и построить электронную модель системы, имеющей матрицы состояния:

; C= .

Задача 3. Начертить блок-схему и написать уравнения состояния системы, описываемой дифференциальным уравнением , где g - входная величина; y - выходная величина.

Задача 4. Построить линейную амплитудную характеристику и линейную фазовую характеристику системы, описываемой передаточной функцией W(p)=100/(0.1p+1)(0.01p+1).

Задача 5. О пределить передаточную функцию минимально-фазового устройства, л.а.х. которого представлена ниже

Рис. 1. Логарифмическая амплитудночастотная характеристика устройства

Задача 6. П ользуясь правилами структурных преобразований привести представленную на рис.3.4. структурную схему замкнутой многоконтурной системы к одноконтурной и найти передаточные функции:

Рис.2. Структурная схема многоконтурной САУ

Задача 7. Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой .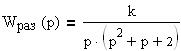

Задача 8. Определить количество правых корней m системы третьего порядка, годограф Михайлова которой имеет вид

Рис.1. Годограф Михайлова

Задача 9. Определить порядки астатизма по управляющему g(t) и возмущающему f(t) воздействиям САУ, структурная схема которой приведена на рис.1.

Рис.1. Структурная схема САУ

Задача 10. Определить предельное значение коэффициента передачи k нелинейного элемента из условия обеспечения абсолютной устойчивости нелинейной системы, передаточная функция линейной части которой

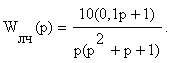
Задача 11. Определить возможную частоту автоколебаний при введении в САУ, имеющей ЛЧХ вида (рис.1), однозначной нелинейности в виде двухпозиционного реле.

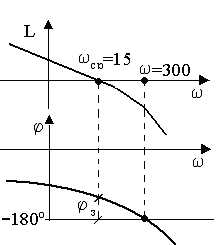
Рис.1. ЛЧХ линейной части

Задача 12. Изобразить фазовые траектории для нелинейной системы с тремя различными нелинейностями - двухпозиционное реле, трехпозиционное реле с зоной нечувствительности (±0,2) и двухпозиционное реле с гистерезисом

(±0,1), если линейная часть имеет передаточную функцию. Примем для всех нелинейностей величину сигнала на выходе реле ±2.

Задача 13. На рис.1 представлены АФХ -1/W_нэ(A) и W_лч(jω). Кроме того в нее вводится звено чистого запаздывания. Определить критическое время чистого запаздывания, при котором в нелинейной системе возникают автоколебания.

Рис.1. АФХ нелинейности -1/W_нэ(A) и линейной части W_лч(jω)

Задача 14. Определить дискретную передаточную функцию системы, непрерывная часть которой состоит из ПИ - регулятора и нейтрального

объекта, а в качестве импульсного элемента используется экстраполятор нулевого порядка и экстраполятор с АИМ 1-го рода. Принять период дискретности Т₀=2с, общий коэффициент усиления К=20 с^-2, постоянную времени τ=5 с, импульсы длительности γ=0,2 с.

Задача 15. Построить логарифмические частотные характеристики импульсной системы с экстраполятором нулевого порядка, период дискретности которой T_o=2с, а передаточная функция непрерывной части

.

Задача 16. Дать заключение об устойчивости импульсной системы, характеристическое уравнение которой D(z)=10z³+4z²+6z+2+0.

Задача 17. Определить скоростную ошибку регулирования импульсной системы при подаче на вход управляющего воздействия g(t)=g₁t, если ее разомкнутая передаточная функция

Период квантования Т_о=2 с.

Задача 18. Определить скоростную ошибку регулирования импульсной системы при подаче на вход управляющего воздействия g(t)=g₁t, если ее разомкнутая передаточная функция

Задача 19. Пусть передаточная функция разомкнутой системы W(p)=k/(p(Tp+1)). На САУ подается полезный сигнал g(t)=g₁t и помеха "белый шум" со спектральной плотностью S_f(ω)=N. Определить систематическую ошибку m_ε и среднеквадратическую ошибку σ. Структурная схема представлена на рис.1.

Рис.1. САУ со случайным сигналом

Задача 20. Оценить свойства управляемости и наблюдаемости САУ, заданной уравнениями состояния

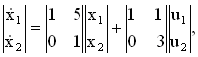
где:

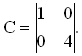
Задача 21. Определить управляемость САУ третьего порядка n=3 с одним управляющим воздействием m=1, представленных уравнениями состояния x=Ax + Bu с матрицами системы А и В вида

Задача 22. Написать уравнения состояния и построить электронную модель системы, имеющей матрицы состояния:

; C= .

Задача 23. Начертить блок-схему и написать уравнения состояния системы,

описываемой дифференциальным уравнением:

,

где u - входная величина; y - выходная величина.

Задача 24. Начертить блок-схему и написать уравнения состояния системы, описываемой дифференциальным уравнением , где u - входная величина; Z - выходная величина.

Задача 25. О пределить передаточную функцию минимально-фазового устройства, л.а.х. которого представлена ниже

Рис. 1. Логарифмическая амплитудночастотная характеристика устройства

Задача 26. П ользуясь правилами структурных преобразований привести представленную на рис.3.4. структурную схему замкнутой многоконтурной системы к одноконтурной и найти передаточные функции:

Рис.2. Структурная схема многоконтурной САУ

Задача 27. Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой .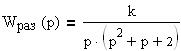

Задача 28. Определить количество правых корней m системы третьего порядка, годограф Михайлова которой имеет вид

Рис.1. Годограф Михайлова

Задачи 1-28. По принципиальной схеме звенев систем автоматического управления (Рис. 1-28)

составить дифференциальные уравнения звеньев, преобразовать уравнения в параметрический вид по Лапласу, определить передаточные функции звеньев. Найти временные или частотные характеристики звеньев САУ по указанию преподавателя.

Рис. 1-28. Варианты заданий.

Дата добавления: 2015-08-02