Электрический ток. Сила и плотность тока

Электрическим током называется направленное (упорядоченное) движение заряженных частиц.

Электрический ток в проводниках различного рода представляет собой либо направленное движение электронов в металлах (проводники первого рода), имеющих отрицательный заряд, либо направленное движение более крупных частиц вещества — ионов, имеющих как положительный, так и отрицательный заряд — в электролитах (проводники второго рода), либо направленное движение электронов и ионов обоих знаков в ионизированных газах (проводники третьего рода).

За направление электрического тока условно принято направление движения положительно заряженных частиц.

Для существования электрического тока в веществе необходимо:

1. наличие заряженных частиц, способных свободно перемещаться по проводнику под действием сил электрического поля:
2. наличие источника тока, создающего и поддерживающего в проводнике в течение длительного времени электрическое поле;

Количественными характеристиками электрического тока являются сила тока I и плотность тока j.

Сила тока — скалярная физическая величина, определяемая отношением заряда Δq, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, к этому промежутку времени.

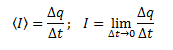
Единицей силы тока в СИ является ампер (А).

Если сила тока и его направление со временем не изменяются, то ток называется постоянным.

Единица силы тока — основная единица в СИ 1 А — есть сила такого неизменяющегося тока, который, проходя по двум бесконечно длинным параллельным прямолинейным проводникам очень маленького сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает силу взаимодействия между ними 2·10-7 Η на каждый метр длины проводников.

Плотность тока j — это векторная физическая величина, модуль которой определяется отношением силы тока I в проводнике к площади S поперечного сечения проводника, т.е.

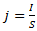
В СИ единицей плотности тока является ампер на квадратный метр (А/м2).

Как следует из формулы (1), 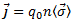. Направление вектора плотности тока 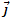совпадает с направлением вектора скорости упорядоченного движения 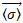положительно заряженных частиц. Плотность постоянного тока постоянна по всему поперечному сечению проводника.

Вопрос 19

Вопрос 20

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

где R = const.

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)

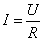
(7.6.1)

Для однородного линейного проводника выразим R через ρ:

,

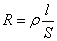(7.6.2)

ρ – удельное объемное сопротивление; [ρ] = [Ом·м].

Найдем связь между 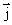и 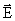в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.

В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока 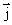и вектор напряженности поля 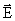коллинеарны (рис. 7.6).

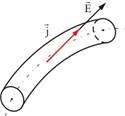
Рис. 7.6

Исходя из закона Ома (7.6.1), имеем:

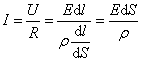
А мы знаем, что 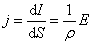или 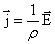. Отсюда можно записать

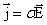
это запись закона Ома в дифференциальной форме.

Здесь 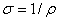– удельная электропроводность.

Размерность σ – [ ].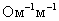

Полную цепь можно рассматривать как последовательное соединение сопротивления внешней цепи и внутреннего сопротивления источника тока. Полное сопротивление цепи представляет собой сумму внутреннего сопротивления источника и сопротивления внешней цепи. Заменим элемент каким-либо другим, имеющим такое же внутреннее сопротивление, но другую э. д. с. Мы обнаружим, что ток при этом изменится.
Таким образом, ток в цепи зависит от э. д. с. источника и от полного сопротивления цепи.
Количественный закон, связывающий эти величины, представляет закон Ома для замкнутой цепи: ток в цепи, содержащей источник тока, прямо пропорционален э. д. с. источника и обратно пропорционален полному сопротивлению цепи.

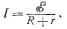(80.1)

Вопрос 22

Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд 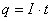. Это равносильно тому, что заряд q переносится за время t из одного конца проводника в другой.

При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу . Разделив работу на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке .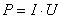

Эта мощность может расходоваться на совершение работы над внешними телами; на протекание химических реакций; на нагревание данного участка цепи и др.

В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло

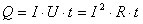(4.1)

Это соотношение называется законом Джоуля - Ленца. Оно было экспериментально установлено английским физиком Д. П. Джоулем и подтверждено точными опытами Э. Х. Ленца.

Если сила тока изменяется со временем, то количество теплоты, выделяющееся в проводнике за время t, вычисляется по формуле

.

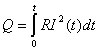От формулы (4.1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля - Ленца, за время d t, в этом объеме выделится количество теплоты

.

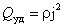Величину 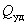называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля - Ленца.

Вопрос 23

Вопрос 24

В 1820 г. французские физики Жан Батист Био и Феликс Савар, провели исследования магнитных полей токов различной формы. А французский математик Пьер Лаплас обобщил эти исследования. Он проанализировал экспериментальные данные и сделал вывод, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока:

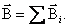
Элемент тока длины d l (рис. 1.4) создает поле с магнитной индукцией:

,

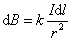(1.2.1)

или в векторной форме:

,

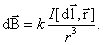(1.2.2)

Это и есть закон Био–Савара–Лапласа, полученный экспериментально.

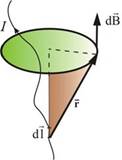
Рис. 1.4

Здесь I – ток; 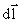– вектор, совпадающий с элементарным участком тока и направленный в ту сторону, куда течет ток; 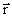– радиус-вектор, проведенный от элемента тока в точку, в которой мы определяем 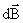; r – модуль радиус-вектора; k – коэффициент пропорциональности, зависящий от системы единиц.

Как видно из рисунка, вектор магнитной индукции 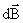направлен перпендикулярно плоскости, проходящей через 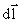и точку, в которой вычисляется поле.

Направление 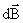связано с направлением 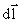«правилом буравчика»: направление вращения головки винта дает направление 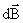, поступательное движение винта соответствует направлению тока в элементе.

Таким образом, закон Био–Савара–Лапласа устанавливает величину и направление вектора 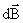в произвольной точке магнитного поля, созданного проводником 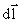с током I.

Модуль вектора 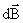определяется соотношением:

,

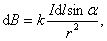(1.2.3)

где α – угол между 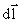и 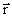; k – коэффициент пропорциональности, зависящий от системы единиц.

В международной системе единиц СИ закон Био–Савара–Лапласа для вакуума можно записать так:

,

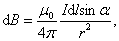(1.2.4)

где 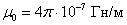– магнитная постоянная.

Вопрос 25

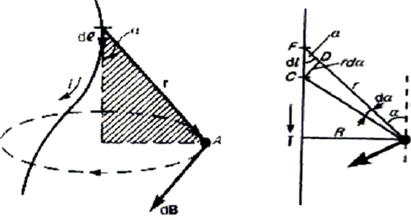
Рис. 1.2. К выводу закона Био–Савара–Лапласа

Вектор dB направлен в точке A перпендикулярно плоскости векторов dl и r по правилу буравчика и совпадает с касательной к линии магнитной индукции.

Магнитное поле прямого тока – тока, текущего по тонкому прямому проводу бесконечной длины. В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей.
В качестве постоянной интегрирования выберем угол  (угол между векторами dl и r), выразив через него все остальные величины. Из рис.1.2 следует, что

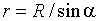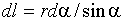, (1.6)

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (1.5), получим, что магнитная индук­ция, создаваемая одним элементом проводника, равна:

.

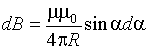Так как угол α для всех элементов прямого тока изменяется в пределах от 0 до , то, согласно (1.4) и (1.6),

.

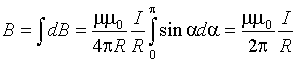Следовательно, магнитная индукция поля прямого тока

.

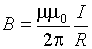Магнитное поле в центре кругового проводника с током (рис. 1.3).

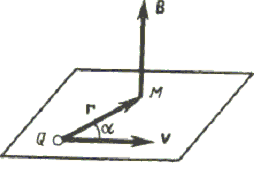
Рис. 1.3. Ориентация векторов B, r и v

Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления – вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin = 1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то

^.

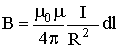Тогда

.

Следовательно, магнитная индукция поля в центре кругового проводника с током:

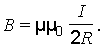
Вопрос 27

---

Дата добавления: 2015-08-10