Цифровая фильтрация

Рассмотрим простейшее скользящее усреднение.

Фильтр, усредняющий входной дискретизированный сигнал x [ n ] (трёхточечный фильтр), описывается выражением

.

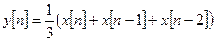Если сместить переменную n на один отсчет, то это выражение принимает вид

.

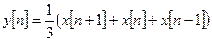Соответственно пятиточечный фильтр определяется уравнением

.

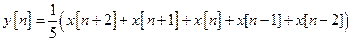Описываемые фильтры называются нерекурсивными или трансверсальными.

Приведенные выше уравнения удобно исследовать с помощью дискретного преобразования Лапласа, или Z – преобразования:

;

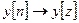Известны основные свойства этого преобразования:

; ; ;

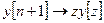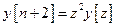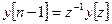С учетом этих свойств пятиточечный фильтр опишется выражением

;

а его передаточная функция имеет вид

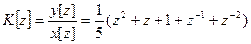. (1)

На практике представляет интерес прохождение через фильтр сигнала определенной формы, в качестве которого наиболее распространен скачкообразный сигнал, а также гармонический сигнал.

При использовании гармонического сигнала свойства фильтра определяются его амплитудно – частотной (АЧХ) и фазо – частотной (ФЧХ) характеристиками.

Известно, что комплексная частотная характеристика фильтра определяется при подстановке

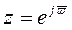, (2)

где 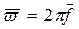- круговая частота дисретизированного гармонического сигнала,

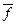- его частота.

Эта частота определяется соотношением

,

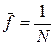где N – число дискретных отсчётов на периоде преобразуемого сигнала (рис.1)

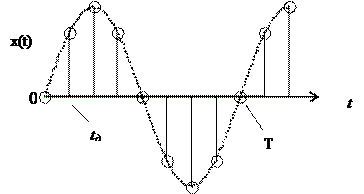Рис.1. Дискретизация сигнала.

Для сигнала, изображенного на рис.1, N=8.

Очевидно,

;

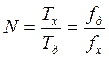где Т_х – период сигнала, Т_д – период дисретизации, f_x, f_д - их частоты соответственно.

Тогда приведенная частота дискретизированного сигнала определяется выражением

.

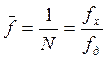При подстановке (2) в выражение (1) для пятиточечного усреднения получаем:

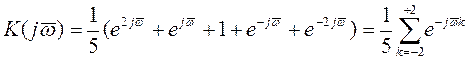(3)

В общем случае для М – точечного усреднения имеем выражение

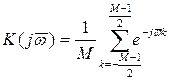(4)

Преобразовывая выражение (3)в тригонометрическую форму, получаем:

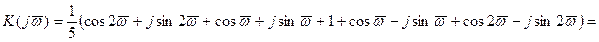
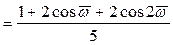(5)

Таким образом, мнимая составляющая этой комплексной функции равна нулю. Это означает, что АЧХ фильтра определяется (5), а ФЧХ фильтра равна нулю.

В общем случае (при несимметричном виде весовой функции фильтра) комплексная функция фильтра может содержать как действительную, так и мнимую составляющие, т.е. иметь вид

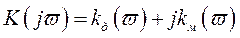
В этом случае амплитудно - частотная характеристика фильтра определяется выражением

.

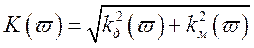На практике получила распространение АЧХ в виде

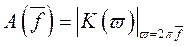
Такая АЧХ для пятиточечного усредняющего фильтра определяется выражением

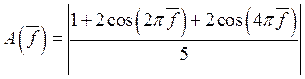. (6)

График этой АЧХ вид, изображенный на рис.2.

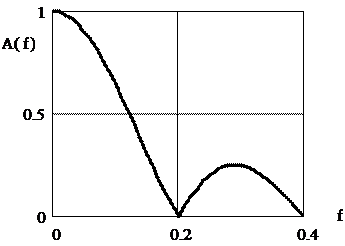Рис.2. АЧХ пятиточечного усредняющего фильтра.

Частота, на которой значение АЧХ равно нулю, называется частотой режекции.

Очевидно, что первая частота режекции пятиточечного усредняющего фильтра равна 0.2, что соответствует пяти дискретным отсчетам на периоде сигнала.

Из рассмотрения этого графика видно, что чем меньше частота дискретизированного сигнала, тем ближе к единичному значению функция , тем меньше фильтр искажает амплитуду входного сигнала.

На практике число точек усреднения может доходить до нескольких десятков.

Цифровой фильтр, функция которого изображена на рис.3а, использует четное число дискретных значений сигнала, определенных на середине интервалов его дискретизации.

Функция, изображенная на рис.3б, соответствует цифровому фильтру, использующему нечетное число дискретных значений сигнала, определенных на границах интервалов его дискретизации.

n +1/2

b [ m ] b [ m ]

n -1/2

n +3/2

n -3/2

n k (n-2)(n-1) n (n+1)(n+2) k

(n-2)(n-1)(n+1)(n+2)

Рисунок 3а – Характеристика Рисунок 3б - Характеристика

фильтра с четным (6) числом точек фильтра с нечетным (5) числом точек

Цифровой фильтр, весовая функция которого изображена на рис.3а, в общем случае определяется выражением

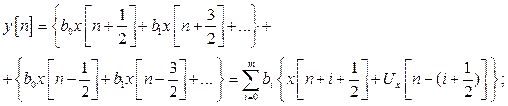(7)

где - дискретные значения сигнала, аппроксимация которых определяется цифровым фильтром;

b_i – коэффициенты весовой функции фильтра;

m - параметр, соответствующий половине числа значений весовой функции фильтра.

Фильтр с нечетным числом используемых данных, весовая функция которого изображена на рис.3б, определяется выражением

(8)

Примером такого фильтра являются описанные выше трех – и пятиточечные (1) фильтры скользящего сглаживания.

Дата добавления: 2015-07-21