Основные понятия [4].

Основные термины математического моделирования. Уточним определения основных терминов математических моделей:

- компоненты системы, которые могут быть вычленены из нее и рассмотрены отдельно;

- независимые переменные, это внешние величины, которые могут изменяться и не зависят от процессов в системе;

- зависимые переменные, значения этих переменных есть результат воздействия на систему независимых внешних переменных;

- управляемые переменные, значения которых могут изменяться пользователем;

- эндогенные переменные, их значения определяются в ходе деятельности внутренних компонент системы;

- экзогенные переменные определяются пользователем и действуют на систему извне.

Построение моделей. При построении любой модели процесса управления желательно придерживаться следующего плана действий:

1) Сформулировать цели изучения системы.

2) Установить наиболее существенные для данной задачи факторы, компоненты и переменные.

3) Учесть тем или иным способом посторонние, не включенные в модель факторы.

4) Осуществить оценку результатов, проверку модели, оценку полноты модели.

Виды моделей. Модели можно делить на следующие виды:

1) Функциональные модели - выражают прямые зависимости между эндогенными и экзогенными переменными.

2) Модели, выраженные с помощью систем уравнений относительно эндогенных величин.

3) Модели оптимизационного типа. Основная часть модели - система уравнений относительно эндогенных переменных. Цель - найти оптимальное решение для некоторого показателя.

4) Имитационные модели - весьма точное отображение процесса или явления. Математические уравнения при этом могут содержать сложные, нелинейные, стохастические зависимости.

С другой стороны, модели можно делить на управляемые и прогнозные. Управляемые модели отвечают на вопрос: “Что будет, если...?”; “Как достичь желаемого?”, и содержат три группы переменных:

1) переменные, характеризующие текущее состояние объекта;

2) управляющие воздействия - переменные, влияющие на изменение этого состояния и поддающиеся целенаправленному выбору;

3) исходные данные и внешние воздействия, т.е. параметры, задаваемые извне, и начальные параметры.

В прогнозных моделях управление не выделено явно. Они отвечают на вопросы: “Что будет, если все останется по-старому?”

Модели можно делить по способу измерения времени на непрерывные и дискретные. В любом случае, если в модели присутствует время, то модель называется динамической. Чаще всего в моделях используется дискретное время, т.к. информация поступает дискретно. Но с формальной точки зрения непрерывная модель может оказаться более простой для изучения.

Имитационные системы занимают в моделировании особое место. В принципе, любая модель имитационная, ибо она имитирует реальность. Основа имитации (смысл которой мы будем понимать как анализ явления с помощью вариантных расчетов) - это математическая модель. Имитационная система - это совокупность моделей, имитирующих протекание изучаемого процесса, объединенная со специальной системой вспомогательных программ и информационной базой, позволяющих достаточно просто и оперативно реализовать вариантные расчеты. Таким образом, под имитацией понимается численный метод проведения машинных экспериментов с математическими моделями, описывающими поведение сложных систем в течение продолжительных периодов времени, при этом имитационный эксперимент состоит из следующих шести этапов:

1) формулировка задачи,

2) построение математической модели,

3) составление программы для ЭВМ,

4) оценка пригодности модели,

5) планирование эксперимента,

6) обработка результатов эксперимента.

Математические методы управления можно разделить на несколько групп:

- методы оптимизации,

- методы, учитывающие неопределенность, вероятностно-статистические методы,

- методы построения и анализа имитационных моделей,

- методы анализа конфликтных ситуаций (теории игр).

Во всех этих группах можно выделить статическую и динамическую постановки. При наличии фактора времени используют дифференциальные уравнения и разностные методы.

Теория игр (более подходящее название - теория конфликтных ситуаций) зародилась как теория рационального поведения двух игроков с противоположными интересами. Применяется, в основном, для социально-экономических систем управления. Она наиболее проста, когда каждый из них стремится минимизировать свой средний проигрыш, т.е. максимизировать свой средний выигрыш. Отсюда ясно, что теория игр склонна излишне упрощать реальное поведение в ситуации конфликта. Участники конфликта могут оценивать свой риск по иным критериям. В случае нескольких игроков возможны коалиции. Большое значение имеет устойчивость точек равновесия и коалиций.

Методология моделирования. Моделирование процессов управления предполагает последовательное осуществление трех этапов исследования. Первый - от исходной практической проблемы до теоретической чисто математической задачи. Второй – математическое изучение и решение этой задачи. Третий – переход от математических выводов обратно к практической проблеме.

Задача исследований, как правило, порождена потребностями той или иной прикладной области. Вполне понятно, что при этом происходит одна из возможных математических формализаций реальной ситуации. Например, при изучении предпочтений потребителей у экономистов - маркетологов возникает вопрос: различаются ли мнения двух групп потребителей. Мнения потребителей в каждой группе обычно моделируются как независимые случайные выборки, т.е. как совокупности независимых одинаково распределенных случайных величин, а вопрос маркетологов переформулируется в рамках этой модели как вопрос о проверке той или иной статистической гипотезы однородности. Речь может идти об однородности характеристик, например, о проверке равенства математических ожиданий, или о полной (абсолютной) однородности, т.е. о совпадении функций распределения, соответствующих двух совокупностям.

Важно подчеркнуть, что выделение перечня задач находится вне математики. Выражаясь инженерным языком, этот перечень является сутью технического задания, которое специалисты различных областей деятельности дают специалистам по математическому моделированию.

Методологический анализ открывает этап моделирования процессов управления, да и вообще любого исследования. Он определяет исходные постановки для теоретической проработки, а потому во многом и успех всего исследования. Анализ динамики развития методов моделирования позволяет выделить наиболее перспективные методы. В частности, при вероятностно-статистическом моделировании наиболее перспективными оказались методы нечисловой статистики.

Метод исследований, используемый в рамках определенной математической модели - это уже во многом дело математиков. В эконометрических моделях речь идет, например, о методе оценивания, о методе проверки гипотезы, о методе доказательства той или иной теоремы, и т.д. В первых двух случаях алгоритмы разрабатываются и исследуются математиками, но используются прикладниками, в то время как метод доказательства касается лишь самих математиков.

Ясно, что для решения той или иной задачи в рамках одной и той же принятой исследователем модели может быть предложено много методов. В настоящее время для решения практически важных задач могут быть использованы современные информационные технологии на основе метода статистических испытаний и соответствующих датчиков псевдослучайных чисел. Они уже заметно потеснили асимптотические методы математической статистики.

Условия применимости - последний элемент. Он полностью математический. С точки зрения математика замена условия кусочной дифференцируемости некоторой функции на условие ее непрерывности может представляться существенным научным достижением, в то время как прикладник оценить это достижение не сможет. Для него непрерывные функции мало отличаются от кусочно-дифференцируемых.

6.2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ ДИСКРЕТНОГО УПРАВЛЕНИЯ [1, 11, 12]

Дискретно представляемые сигналы описываются функциями дискретной переменной. Для описания дискретных систем используются решетчатые функции и разностные уравнения. Решетчатые функции являются аналогами непрерывных функций, описывающих непрерывные системы, а разностные уравнения являются аналогами дифференциальных уравнений.

Решетчатой функцией называется функция, получающаяся в результате замены непрерывной переменной на дискретную независимую переменную, определенную в дискретные моменты времени kТ, k = 0, 1, 2, … Непрерывной функции x(t) соответствует решетчатая функция х(kТ), где Т – период квантования, при этом непрерывная функция является огибающей решетчатой функции. При заданном значении периода квантования Т непрерывной функции x(t) соответствует однозначная решетчатая функция х(kТ). Однако обратного однозначного соответствия между решетчатой и непрерывной функцией не существует, так как через ординаты решетчатой функции можно провести множество огибающих.

Отсчеты по шкале времени удобно вести в целочисленных единицах периода квантования Т. С этой целью вместо переменной t непрерывной функции введем новую переменную t=t/T, при этом непрерывной функции x(t) будет соответствовать решетчатая функция х(k) º x_k.

Теорема Котельникова-Шеннона. Процедура преобразования сигнала непрерывного времени x(t) к дискретному виду, квантованному по времени, называется квантованием. Такая процедура отражает как реальные процессы, проходящие в цифровых системах управления, так и математические операции, использующиеся в различных сферах теории информации. В результате квантования получается импульсная последовательность x(kT) (решетчатая функция), которая при t = kT совпадает с исходным сигналом:

x(kT) = x(t)|_t=kT,

и не определена во все другие моменты времени, т.е. между отсчетами k. Потери информации при квантовании зависят от величины интервала квантования Т (частоты квантования 2p/T).

Выбор интервала Т обычно осуществляется из соображений теоретической возможности точного восстановления исходного сигнала по импульсной последовательности (дискретной выборке). Согласно теореме Котельникова-Шеннона, если спектр сигнала x(t) ограничен максимальной частотой w_max, то точное восстановление функции x(t) теоретически возможно при условии, что частота квантования w более чем в 2 раза превосходит наибольшую частоту w_max:

w ≥ 2w_max, T < p/w_max.

Разностные уравнения. Связь между значениями решетчатой функции при разных значениях аргумента определяется с помощью конечных разностей, которые являются аналогами производных в дифференциальных уравнениях.

Разностью первого порядка, или первой разностью, называется разность между последующим дискретным значением решетчатой функции и ее текущим значением:

Dx(k) = x(k+1) – x(k).

Разность первого порядка характеризует скорость изменения решетчатой функции и, следовательно, является аналогом первой производной непрерывной функции.

Разность второго порядка определяется как разность двух соседних разностей первого порядка:

D²x(k) = Dx(k+1) - Dx(k) = [x(k+2)-x(k+1)] – [x(k+1)-x(k)] = x(k+2) - 2x(k+1) + x(k).

Продолжая аналогично, для разности любого m-го порядка будем иметь:

D^mx(k) = D^m-1x(k+1) - D^m-1x(k).

D^mx(k) = 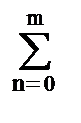(-1)ⁿ x(k+m-n) m!/[k!(m-n)!].

Дискретизация автономных систем. Под дискретизацией системы подразумевается преобразование непрерывной динамической модели к дискретной форме описания - одной из форм разностных уравнений. При этом предполагается, что в моменты t = kT импульсные сигналы x(kT) полученной дискретной модели с определенной степенью точности повторяют значения сигналов x(t) исходной непрерывной системы.

C использованием разностных уравнений математическое описание линейных импульсных систем приводится к виду:

a_mD^mx(k) + a_m-1D^m-1x(k) +…+ a₀ x(k) = 0. (6.2.1)

где уравнение (6.2.1) является линейным разностным уравнением с постоянными коэффициентами а_m (m=0, 1, 2,...), - аналог однородного линейного дифференциального уравнения при описании непрерывных динамических систем. Решение (6.2.1) дает значение дискретной переменной х(k) для каждого периода квантования.

Уравнение (6.2.1) можно записать в виде:

c_n x(k+n) = 0. (6.2.2)

Таким образом, в дискретной системе (6.2.1) процессы в квантованные моменты времени t-kT точно совпадают с процессами в исходной непрерывной системе. Так как решения дискретной системы в промежуточные моменты времени не определены, то корректный переход к дискретной форме предусматривает выбор интервала квантования Т в соответствии с теоремой Котельникова-Шеннона.

Дискретное z-преобразование. В теории импульсных систем для решения разностных уравнений используется дискретное преобразование Лапласа и его модификация - дискретное z-преобразование.

Преобразование Лапласа для непрерывной функции х(t):

X(р) = x(t) exp(-pt) dt. (6.2.3)

При переходе к дискретной функции x(kТ), заменяя интегрирование суммированием:

X(p) =T 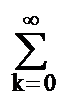x(kT) exp(-pkT). (6.2.4)

Введем новую переменную z=exp(pt):

X(z) =T 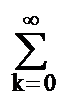x(kT) z^-k. (6.2.5)

Это уравнение представляет собой дискретное преобразование Лапласа, в котором выражение

X(z) = 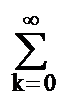x(kT) z^-k. (6.2.6)

называется z-преобразованием. Оно лежит в основе метода решения разностных уравнений. Как видно из этих выражений, дискретное преобразование Лапласа X(z) отличается от z-преобразования наличием нормирующего множителя Т.

При анализе непрерывных систем преобразование Лапласа позволяет перейти от дифференциальных уравнений к более простым алгебраическим. При анализе дискретных систем z-преобразование позволяет перейти от разностных уравнений к алгебраическим и существенно упростить анализ динамики дискретных систем.

В выражении (6.2.6) функция х(kТ) называется оригиналом решетчатой функции, a X(z) – ее изображением. Для обратного перехода от изображения к оригиналу (для нахождения исходной решетчатой функции по ее изображению) используется обратное z-преобразование:

x(kT) = (1/2pj) ∮ X(z) z^k-1 dz.

Экспоненциальная зависимость матриц уравнений состояния непрерывной и дискретной систем позволяет сделать важный вывод о связи их собственных значений, а значит и корней соответствующих характеристических полиномов. Корни p_i характеристического полинома непрерывной системы связаны с корнями z_i характеристического полинома эквивалентной дискретной системы соотношением

z_i = exp(Tp_i). (6.2.7)

В общем случае, отображение (6.2.7) не однозначно, и нескольким различным значениям p_i может соответствовать одно и то же значение z_i. Взаимно-однозначное соответствие корней непрерывной и эквивалентной дискретной систем выполняется только при интервале дискретизации, удовлетворяющем теореме Котельникова-Шеннона.

Преобразователь непрерывного сигнала в цифровой код. АЦП осуществляет три операции: квантование сигнала по времени, квантование по уровню и кодирование. Квантование по времени заключается в измерении непрерывной величины х(t) в дискретные моменты времени t_k=kDt, Dt=const, k=0, 1, 2,…, и осуществляется импульсным элементом - ИЭ. На выходе импульсного элемента получается решетчатая функция x(t_k). Период квантования по времени зависит от спектральной характеристики непрерывного сигнала и определяется теоремой Котельникова.

Рис. 6.2.1.

Процесс квантования решетчатой функции х(t_k) по уровню можно представить как прохождение сигнала х(t_k) через нелинейный элемент с многоступенчатой релейной характеристикой - квантователь по уровню КУ (рис. 6.2.1). В результате квантования по уровню точно измеренные значения сигнала х(t_k) заменяются приближенными ближайшими дискретными значениями х_k º x(k) @ x(t_k), т. е. процесс квантования по уровню равносилен округлению сигнала х(t_k) до целых значений. Шаг квантования d_k, характеризует точность преобразователя.

Учет квантования по уровню приводит к необходимости рассмотрения нелинейных цифровых систем. Анализ систем упрощается, если элемент с многоступенчатой релейной характеристикой представить в виде параллельного соединения линейного усилительного элемента с коэффициентом K = 1, характеристика которого изображена на рис.6.2.1 справа, и нелинейного элемента с характеристикой d(k), равной разности между линейной и релейной характеристиками. В этом случае квантованный по уровню сигнал можно представить, как сумму точного сигнала х(t_k) и добавочного сигнала d(k), ограниченного по величине половиной ступени квантования:

Прежде чем сигнал х(k) поступает на цифровое вычислительное устройство (ЦВУ) системы, осуществляется его кодирование - преобразование в цифровой код х_ц(k). Если в ЦВУ используется двоичная система счисления, то с помощью кодирующего устройства К каждый импульс, поступающий с квантователя по уровню КУ, преобразуется в двоичный цифровой код, соответствующий амплитуде этого импульса. Двоичные числа представляются в виде последовательности импульсов, разделенных интервалом времени t. Каждому разряду двоичного числа отводится интервал времени t' на выставление кодов 0 или 1 (обычно отсутствие или наличие определенного уровня напряжения).

На ЦВУ числа могут поступать последовательным или параллельным кодом. В первом случае разряды числа идут последовательно друг за другом по одному каналу, как правило, начиная с младшего. Одно число от другого отделяется специальным маркерным импульсом. Минимальный интервал Т передачи числа равен nt, где n - количество разрядов числа. При параллельном коде все разряды числа поступают одновременно (параллельно) по нескольким каналам, число которых равно числу разрядов. Так как при кодировании сигнала не происходит изменения (преобразования) информации, то передаточная функция кодирующего устройства равна единице.

Цифровое вычислительное устройство ЦВУ можно рассматривать как дискретный преобразователь, преобразующий входную последовательность чисел х_ц(k) в выходную y_ц(k) в соответствии с заложенной программой вычислений, представляющей собой алгоритм переработки информации. В дискретной линейной системе связь между входом и выходом (входной и выходной дискретными последовательностями значений сигнала – отсчетами), задается линейным оператором преобразования TL:

y(kDt) = TL{x(kDt)}.

Это выражение отображает краткую запись линейного разностного уравнения:

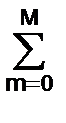a_m y(kDt-mDt) = b_n x(kDt-nDt), (6.2.8)

где k = 0, 1, 2, …- порядковый номер отсчетов, Dt - интервал дискретизации сигнала, a_m и b_n - вещественные или, в общем случае, комплексные коэффициенты. Положим a₀ = 1, что всегда может быть выполнено соответствующей нормировкой уравнения (6.2.8), и, принимая в дальнейшем Dt = 1, т.е. переходя к числовой нумерации цифровых последовательностей значений сигналов, приведем его к виду:

y(k) = b_n x(k-n) – a_m y(k-m). (6.2.9)

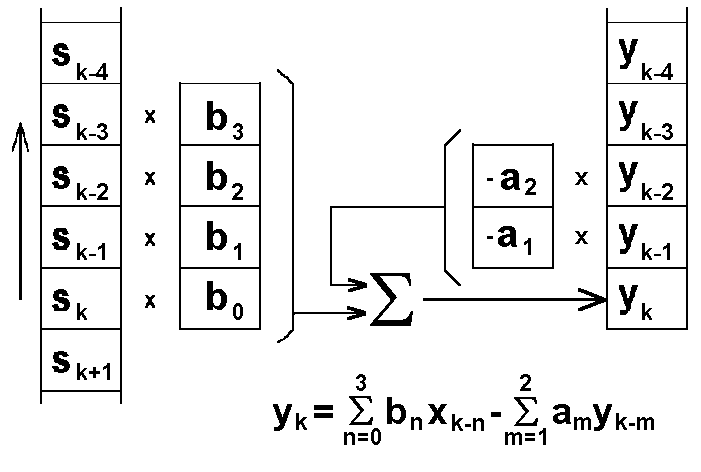Рис. 6.2.2. Рекурсивный ЦФ.

ЦВУ, которые описываются полным разностным уравнением (6.2.9), в теории цифровой обработки данных принято называть рекурсивными цифровыми фильтрами (РЦФ), так как в вычислении текущих выходных значений участвуют не только входные данные, но и значения выходных данных фильтрации, вычисленные в предшествующих циклах расчетов. С учетом последнего фактора рекурсивные фильтры называют также фильтрами с обратной связью, положительной или отрицательной в зависимости от знака суммы коэффициентов a_m. По существу, полное окно рекурсивного фильтра состоит из двух составляющих: нерекурсивной части b_n, ограниченной в работе текущими и "прошлыми" значениями входного сигнала, и рекурсивной части a_m, которая работает только с "прошлыми" значениями выходного сигнала. Техника вычислений для РЦФ приведена на рис. 6.2.2.

Передаточные функции ЦВУ. Удобным методом решения разностных уравнений линейных систем является z-преобразование. Применяя z-преобразование к обеим частям равенства (6.2.8), c учетом сдвига функций (y(k-m) ó z^-m Y(z)), получаем:

Y(z) 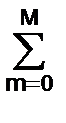a_mz^-m = X(z) b_nz^-n, (6.2.10)

где X(z),Y(z)- соответствующие z-образы входного и выходного сигнала. Отсюда, полагая a_o = 1, получаем в общей форме функцию связи выхода фильтра с его входом - уравнение передаточной функции системы в z-области:

H(z) = Y(z)/X(z) = b_nz^-n (1+ a_mz^-m). (6.2.11)

Для нерекурсивных ЦВУ, при нулевых коэффициентах a_m:

H(z) = b_nz^-n. (6.2.12)

При проектировании фильтров исходной, как правило, является частотная передаточная функция фильтра H(ω), по которой вычисляется ее Z-образ H(z) и обратным переходом в пространство сигналов определяется алгоритм обработки данных. В общей форме для выходных сигналов фильтра:

Y(z) = H(z)·X(z).

Y(z)·(1+ a_m z^-m) = X(z) b_n z^-n

Y(z) = X(z) b_n z^-n – Y(z) a_m z^-m. (6.2.13)

После обратного Z-преобразования выражения (6.2.13):

y(k) = b_n x(k-n) – a_m y(k-m). (6.2.14)

При подаче на вход фильтра единичного импульса Кронекера d_о, имеющего z-образ d(z)=z^-n = 1, сигнал на выходе фильтра будет представлять собой импульсную реакцию фильтра y(k) ≡ h(k), при этом:

H(z) = Y(z)/d(z) = Y(z) = TZ[y(k)] = h(k) z^-k, (6.2.15)

т.е. передаточная функция фильтра является z-образом ее импульсной реакции. При обратном z-преобразовании передаточной функции соответственно получаем импульсную характеристику фильтра:

h(k) ó H(z). (6.2.16)

Если функция H(z) представлена конечным степенным полиномом, то обратное z-преобразование осуществляется элементарно идентификацией коэффициентов по степеням z. Передаточная функция РЦФ также может быть представлена степенным полиномом прямым делением числителя на знаменатель правой части выражения (6.2.11), однако результат при этом может оказаться как конечным, так и бесконечным, т.е. система может иметь либо конечную, либо бесконечную импульсную характеристику. Практически используемые рекурсивные фильтры обычно имеют бесконечную импульсную характеристику (БИХ-фильтры) при конечном числе членов алгоритма фильтрации (6.2.14).

Система устойчива, если при любых начальных условиях ее реакция на любое ограниченное воздействие также ограничена. Критерием устойчивости является абсолютная сходимость отсчетов импульсного отклика системы:

|h(n)| < ¥. (6.2.17)

Анализ устойчивости может быть проведен по передаточной функции. В устойчивой системе передаточная функция не должна иметь особых точек (полюсов) на и вне единичного круга на z-плоскости. Отсюда необходимое и достаточное условие устойчивости импульсных систем - модули корней передаточной функции (6.2.11) должны быть меньше 1 (полюса передаточной функции системы внутри единичного круга на z-плоскости). Чем меньше значения модулей корней, тем больше запас устойчивости системы.

Частотные характеристики ЦВУ. От z-образов сигналов и передаточных функций подстановкой z = exp(jwDt) можно перейти к Фурье-образам функций, т.е. к частотным спектрам сигналов и частотной характеристике цифровых систем, а точнее – к функциям их спектральных плотностей.

Передаточная частотная функция (частотная характеристика при а_о=1):

H(w) = A(w)/B(w) = b_n exp(-jwnDt) [1+ a_m exp(-jwmDt)]. (6.2.18)

Частотная характеристика системы представляет собой Фурье-образ его импульсной реакции, и наоборот. При Dt = 1:

H(w) = h(n) exp(-jwn), (6.2.19)

h(n) = (1/2p) H(w) exp(jwn) dw. (6.2.20)

В общем случае H(w) является комплексной функцией, модуль которой R(w) называется амплитудно-частотной характеристикой (АЧХ), а аргумент j(w) – фазово-частотной характеристикой (ФЧХ).

A(w) = |H(w)| =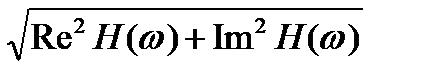

j(w) = arctg(-Im H(w)/Re H(w)).

Выбор знака фазового угла ориентирован на каузальные системы с отрицательным временным запаздыванием сигналов. Допустим, что система осуществляет только сдвиг сигнала x(t) вправо по временной оси, т е. y(t) = x(t-t). Для преобразования Фурье функции y(t) имеем:

Y(f) = 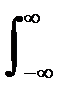y(t) exp(-j2pft) dt = 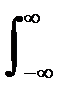x(t-t) exp(-j2pft) dt =

= exp(-j2pft) 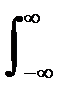x(t) exp(-j2pft) dt = exp(-j2pft) X(f).

Отсюда:

H(f) = Y(f)/X(f) = exp(-j2pft), |H(f)| = 1, j_h(f) = -2pft.

Из последнего равенства следует, что фаза представляет собой прямую с отрицательным тангенсом угла наклона -2pft. Соответственно, для всех каузальных фильтров, осуществляющих преобразование с определенной задержкой сигнала на выходе, при выполнении операции над частотными составляющими сигнала имеет место:

Y(f) = H(f) X(f) = |H(f)| exp(jj_h(f)) |X(f)| exp(jj_x(f)) = |H(f)| |X(f)| exp{j [j_h(f)+j_x(f)]},

|Y(f)| = |H(f)| |X(f)|, j_y(f) = j_h(f)+j_x(f).

C учетом отрицательного знака j_h(f) фазовой характеристики каузальных фильтров это вызывает сдвиг в "минус" всех частотных составляющих сигнала и соответствующую задержку выходного сигнала относительно входного.

6.3. МОДЕЛИ СОСТОЯНИЯ ЛИНЕЙНОЙ ДИСКРЕТНОЙ СИСТЕМЫ [1, 2]

Математические модели дискретных систем управления описывают поведение этих систем только в квантованные моменты времени: t_k, k = 0, 1, 2,... Дискретным представлением непрерывных сигналов u(t), y(t), х(t) являются последовательности:

{u(t_k)}, {y(t_k)}, {х(t_k)}.

Математические модели дискретных систем устанавливают взаимосвязь между этими последовательностями.

Дискретные автоматические системы управления содержат в своей структуре цифровую (дискретную) и аналоговую (непрерывную) части. Для согласования этих частей в системе используются аналогово-цифровой и цифроаналоговый преобразователи (АЦП и ЦАП). АЦП ставит в соответствие непрерывной функции f(t), t ≥ t₀ последовательность {f(t_k)}=f(kDt), Dt=const, k = 0, 1, 2,…}, которую называют решетчатой функцией f_k. В свою очередь, ЦАП осуществляет преобразование последовательности {f_k, k = 0, 1, 2,...} в некоторую непрерывную функцию, которая является аппроксимацией исходной функции f(t), t ≥ t₀. Часто используют кусочно-постоянную аппроксимацию, поэтому такой преобразователь называют экстраполятором, или фиксатором нулевого порядка.

Построение дискретного представления непрерывной системы носит название процесса дискретизации, или квантования, непрерывной системы. Пусть непрерывная система представлена своей внешней моделью:

А₀ y⁽ⁿ⁾(t) + А₁ y^(n-1)(t) + А₂ y^(n-2)(t) + … + А_n y(t) = u(t). (6.3.1)

При достаточно малом шаге квантования дискретизацию этой модели можно выполнить с необходимой точностью путем замены дифференциалов конечными разностями:

y'(t) = dy(t_k)/dt = Dy(t_k)/Dt = Dt^-1 (y(t_k+1) – y(t_k)),

y"(t) = d²y(t_k)/d²t = D²y(t_k)/D²t = Dt^-1 (Dy(t_k+1) – Dy(t_k)) = Dt^-2 (y(t_k+2) – 2y(t_k+1) + y(t_k)),

… и т.д.

После подстановки в (6.3.1) дискретная внешняя модель системы принимает конечно-разностный вид, который после алгебраических преобразований переводится в рекуррентную форму с постоянными коэффициентами модели a_i:

a₀ y(k+n) + a₁ y(k+n-1) + a₂ y(k+n-2) + … + a_n y(k) = u(k), (6.3.2)

В общем случае функция u(k) также может представлять собой полином:

a₀ y(k+n) + a₁ y(k+n-1) +…+ a_n y(k) = b₁ u(k+n-1) +…+ b_n u(k). (6.3.3)

Движение дискретной модели, представленной в разностном виде, складывается из двух движений: собственного и вынужденного под действием внешнего возмущения. Собственное движение - решение однородного разностного уравнения системы. Общий вид этого решения определяется как линейная форма от собственных чисел системы:

y(k) = C₁ l₁^k + C₂ l₂^k + … + C_n l_n^k, (6.3.4)

где С_i - коэффициенты линейной формы, которые вычисляются через начальные состояния системы; l_i - простые действительные корни характеристического уравнения системы:

a₀ lⁿ + a₁ l^n-1 + a₂ l^n-2 + … + a_n = 0. (6.3.5)

Пример. Непрерывная система описывается дифференциальным уравнением:

y"(t) + 5у'(t) + 6у(t) = u(t); у(0) = 1; у'(0) = 0,5.

Выполним с шагом квантования Dt = 0,1 разностную дискретизацию уравнения:

100(у(k+2) – 2y(k+1) + y(k)) + 50(y(k+1) – y(k)) + 6y(k) = u(k).

После преобразований получим искомую дискретную модель в рекуррентном виде:

у(k+2) – 1.5 у(k+1) + 0,56 у(k) = 0,01 u(k).

Характеристическое уравнение системы:

l² - 1.5 l + 0.56 = 0.

Корни уравнения: l₁ = 0.8, l₂ = 0.7. Соответственно, собственное движение модели:

у(k) = С₀ 0.8^k + C₁ 0.7^k.

Постоянные С₀, С₁ найдем, используя координаты начального состояния системы:

у(0) =С₀ + С₁ = 1; у(1) = C₀ 0.8 + C₁ 0.7.

Значение у(1) определим, используя первую разность:

у'(0) = 10 (y(1)-y(0)) = 0.5. y(1) = 1.05

Отсюда: С₀ = 3.5, С₁ = -2.5. y(k) = 3.5 0.8^k – 2.5 0.7^k.

Операторная форма модели (6.3.3) может быть получена введением в рассмотрение оператора сдвига z:

zⁱ y(k) = y(k+i). (6.3.6)

При этом уравнение (6.3.3) легко преобразуется к виду

a(z) y(k) = b(z) u(k), (6.3.7)

a(z) = zⁿ + a₁z^n-1 +... + a_n-1z + a_n, (6.3.8)

b(z) = b₁z^n-1 +... + b_n-1z + b_n. (6.3.9)

Оператор a(z) называется характеристическим полиномом системы (6.3.3), а комплексные числа z_i, i = (1, n) - корни характеристического уравнения a(z)=0, называются полюсами системы. Корни алгебраического уравнения b(z) = 0 называются нулями системы.

Из выражения (6.3.7) следует операторное уравнение связи переменных y(k) и u(k) и оператор передаточной функции дискретной системы:

y(k) = W(z)u(k), (6.3.10)

W(z) = b(z)/a(z). (6.3.11)

Возмущающее воздействие f(k) влияния на объект управления внешней среды рассматривается как дополнительный входной сигнал, при этом линейная модель дискретной системы принимает вид:

a₀ y(k+n) + a₁ y(k+n-1) +…+ a_n y(k) =

= b₁ u(k+n-1) +…+ b_n u(k) + d₁ f(k+n-1) +…+ d_n f(k). (6.3.12)

где d_i - коэффициенты, определяющие влияние на процессы в системе возмущения f(k). После соответствующих преобразований получаем операторную форму модели (6.3.12):

a(z) y(k) = b(z) u(k) + d(z) f(k). (6.3.13)

d(z) = d₁z^n-1 +... + d_n-1z + d_n. (6.3.14)

y(k) = W(z)u(k) + W_f(z) f(k), (6.3.15)

W_f(z) = d(z)/a(z). (6.3.16)

W_f(z) - передаточная функция системы по возмущающему воздействию f(k).

Решение разностных уравнений. Форма (6.3.3) представления моделей дает простой путь для получения рекуррентного решения, т. е. процедуры нахождения текущих значений y(k) по известным значениям функций у и u в предшествующие моменты дискретного времени k. Подставляя в разностное уравнение k+n=k (или n= 0) запишем:

y(k) = -a₁y(k-l) -...- a_ny(k) + b₁u(k-l) + b₂ u(k-2) +... + b_nu(0). (6.3.17)

В общем случае, аналитическое решение уравнения (6.3.3):

y(k) = y_св(k) + y_в(k). (6.3.18)

Выражение содержит вынужденную составляющая y_в(k), соответствующую реакции системы на входное воздействие u(k), и свободную составляющую y_св(k), соответствующую решениям однородного разностного уравнения (автономной дискретной системы):

a₀ y(k+n) + a₁ y(k+n-1) +…+ a_n y(k) = 0 (6.3.19)

при начальных условиях y(0), у(-1),..., у(-n+1).

Поведение системы и свободная составляющая переходного процесса зависят от полюсов системы z_i, которые в общем случае представлены комплексно-сопряженными парами:

z_i,i+1= a_i ∓ jb_i, z_i,i+1= M_i exp(∓ jj_i), M_i =| z_i,i+1|, j_i = arg z_i,i+1. (6.3.20)

y_св(k) = C₁ z₁^k + C₂ z₂^k + … + C_n z_n^k, (6.3.21)

где C_i - неопределенные коэффициенты, зависящие от начальных условий.

Вещественному неотрицательному корню, для которого a_i > 0, b_i = 0, a j_i = 0, соответствует апериодическая составляющая переходного процесса (мода) y(k) = C_i M_i^k, а вещественному отрицательному корню, для которого a_i < 0, b_i = 0, a j_i = p, - колебательная мода y(k) = C_i M_i^k cos kp.

Парам комплексно-сопряженных корней характеристического полинома z_i,i+1= a_i ∓ jb_i, соответствуют колебательные составляющие

y_i,i+1= A_i M_i^k cos (kj_i-j_i),

где A_i, j_i - параметры, зависящие от начальных условий. Если при некоторых начальных значениях имеет место тождество

y_cв(k) = y* = const, k ≥ 0,

то значение у = у* называется положением равновесия системы.

Вынужденная составляющая переходного процесса определяется входным воздействием u(k). Наиболее распространенными входными сигналами дискретных систем являются единичная импульсная последовательность и дельта-функция Кронекера.

Установившийся режим. Рассмотрим поведение модели системы при постоянном входном воздействии u(k) = const и установившуюся составляющую переходного процесса у = у_у = const. В установившемся (статическом) режиме для любых i≥0 выполняется y_y(k+i) = у_у и u(k+i) = u(k), из выражения (6.3.3) находим статическую характеристику дискретной системы:

y_y = (b₁+…+b_n)u(k) /(1+a₁+…+ a_n) = Ku, (6.3.22)

где K - статический коэффициент. Условием существования статической характеристики является 1+a₁+…+ a_n ≠ 0. Система, удовлетворяющая этому условию, называется статической.

Сопоставляя (6.3.22) и (6.3.10), найдем

(b₁+…+b_n) /(1+a₁+…+ a_n) = W(1) = b(1)/a(1).

Следовательно, W(1) = K, и в статическом режиме система описывается уравнением:

у_у = W(1)u.

Элементарные звенья дискретных систем. В качестве элементарных звеньев выделим простейшие блоки дискретной системы, описывающиеся разностными уравнения 1-2-го порядков и удовлетворяющие условию

|z_i| = |l_i{A}| ≤ 1. (6.3.23)

Элементарные звенья 1-го порядка задаются уравнениями

y(k+1) + ay(k) = bu(k). (6.3.24)

Передаточная функция звена и полюс:

W(z) = b/(z+a), z₁ = -a. (6.3.25)

Решение уравнения (6.3.24):

y(k) = y_cв(k) + y_в(k) = (-a)^k y₀ + b 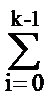(-a)^k-i-1 u(i). (6.3.26)

При b = 1 и a = 0 получаем звено чистого запаздывания (элемент задержки):

y(k+1) = u(k), W(z) = 1/z. (6.3.27)

При а = -1 получаем суммирующее звено (дискретный интегратор):

y(k+1) = y(k) + bu(k), W(z) = b/(z-1). (6.3.28)

Уравнение является дискретным аналогом интегрирующего звена и имеет решение

y(k) = y(0) + b 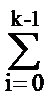u(i). (6.3.29)

Проанализируем свободные составляющие переходных процессов звеньев первого порядка для различных значений параметра а (различных значений полюсов z_i = -a). Для этого рассмотрим автономную систему

y(k+1) + ay(k) = 0, y₀ = y(0). (6.3.30)

Решение уравнения:

y(k) = (-a)^k y₀, (6.3.31)

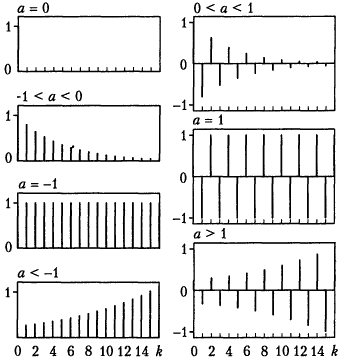Рис. 6.3.1.

Различные реализации функции при y₀ = 1 приведены на рис. 6.3.1.

При z₁ = a = 0 получаем y(k) = 0, k>0, т. е. из произвольного начального положения у₀ процесс сходится к нулевому (равновесному состоянию) за один шаг.

При z₁ = -а ∈ (0,1) имеем (-a)^k →0 при k→∞, и получаем апериодический затухающий процесс: y(k) →0. Звено асимптотически устойчиво.

При z = -а = 1 (суммирующее звено) находим y(k) = y₀, k > 0. Звено нейтрально устойчиво.

Наконец, если z₁ = -а > 1, то при k→ ∞, (-a)^k → ∞, и получаем апериодический расходящийся процесс: |y(k)| → ∞. Звено неустойчиво.

При отрицательных значениях z₁ = -а переходные процессы приобретают колебательный характер. При z₁ = -а ∈ (-1,0) получаем (-a)^k →0 при k → ∞, и затухающий колебательный процесс: y(k) → 0. Звено асимптотически устойчиво.

При z₁ = -а = -1, y(k) = ∓ y₀, k > 0, получаем незатухающий колебательный процесс. Звено нейтрально устойчиво.

Наконец, при z₁ = -а < -1 находим, что при k → ∞, |(-a)^k| → ∞, и получаем расходящийся (неустойчивый) колебательный процесс: |y(k)| → ∞.

Элементарные звенья 2-го порядка. К дискретным звеньям этого типа относятся колебательное и консервативное звено.

Колебательное звено описывается уравнением

y(k +2) - 2M y(k+1) cos j + M² y(k) = b u(k) sin j, (6.3.32)

где M ∈ (0,1), j ∈ (0, p/2). Передаточная функция и комплексно-сопряженные полюсы:

W(z) = b sin j /(z² - 2М z cos j + М²), z_1,2 = M exp(∓jj). (6.3.33)

Звено асимптотически устойчиво и имеет статическую характеристику

y = b sin j /(1 - 2М cos j + М²). (6.3.34)

Консервативное звено (дискретный осциллятор) описывается уравнением

y(k +2) - 2 y(k+1) cos j + y(k) = b u(k) sin j, (6.3.35)

где j ϵ (0, p/2). Передаточная функция и полюсы

W(z) = b sin j /(z² - 2 z cos j + 1²), z_1,2 = exp(∓jj). (6.3.36)

Звено нейтрально устойчиво и не имеет статической характеристики.

Рассмотрим свободные составляющие переходных процессов звеньев второго порядка для различных значений параметра М. Уравнение автономной системы

y(k +2) - 2M y(k+1) cos j + M² y(k) = 0, (6.3.37)

с начальными значениями y(0) = 1 и у(-1) = М^-1 cos j.

Рис. 6.3.2.

Решения уравнения имеют вид

y(k) = M^k cos jk. (6.3.38)

Переходные процессы системы представлены на рис. 6.3.2. Если j < p/2, то полюсы системы имеют положительные вещественные части: Re z_1,2 > 0. При М ϵ (0,1) (колебательное звено) получаем сходящиеся колебательные процессы, при М = 1 (осциллятор) - незатухающий колебательный процесс, а при М > 1 - расходящиеся колебательные процессы.

Аналогично ведут себя и системы, для которых p/2 < j < p, что соответствует отрицательным вещественным полюсам: Re z_1,2 < 0. Основным отличием таких систем является двухчастотный колебательный режим, вызванный переключением знака выходной переменной на каждом шаге k.

Устойчивость дискретных систем. Как и для систем непрерывного времени, под устойчивостью дискретной системы понимают ее способность возвращаться в положение равновесия после окончания действия внешних факторов. Рассматривается свободное движение управляемой системы, либо движение автономной системы при ненулевых начальных условиях.

Автономная система описывается уравнениями

a(z)y(k) = 0, a(z) = z_n + a_l z_n-1 +... + a_n, y_y = y* = 0. (6.3.39)

Понятия устойчивости линейных дискретных систем практически полностью идентичны соответствующим понятиям непрерывных систем. Критерии устойчивости дискретных систем легко выводятся из соответствующих положений непрерывной теории, если принять во внимание, что полюсы z_i дискретной системы связаны с полюсами p_i эквивалентной непрерывной модели соотношением z_i = ехр(Тр_i). Поэтому ограничимся рассмотрением только свойства асимптотической устойчивости.

Устойчивость по выходу (техническая устойчивость) определяется характером изменения выходной переменной y(k), т. е. свойствами решений системы (6.3.39). Система называется асимптотически устойчивой, если выполняется условие

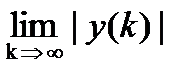= 0.

Основной метод исследования устойчивости дискретных системы предусматривает использование корневых критериев. Дискретная система асимптотически устойчива тогда и только тогда, когда модули всех корней (полюсов) характеристического уравнения системы меньше 1, т.е. |z_i|<1, i=(1,n). Другими словами, полюсы системы на комплексной плоскости должны находиться внутри круга единичного радиуса, при этом окружность единичного радиуса является границей устойчивости. Наличие хотя бы одного корня вне единичного круга делает дискретную систему неустойчивой. Появление одного вещественного или пары двух комплексно-сопряженных корней на единичной окружности при условии расположения остальных корней внутри круга говорит о нейтральной устойчивости дискретной системы (устойчивости по Ляпунову).

Качество дискретных систем управления. Как и для систем непрерывного времени, показатели качества дискретных систем предназначены, для оценки динамических свойств системы, проявляющихся в переходных режимах, и для определения точности, характеризующейся ошибками системы в установившемся режиме, т. е. после окончания переходных процессов.

Динамические показатели качества характеризует поведение свободных составляющих переходного процесса замкнутой системы управления, либо процессов автономной системы. Последние рассматриваются как решения скалярного разностного уравнения (6.3.39). Естественно, что рассматриваются только устойчивые системы.

Динамические показатели качества дискретных систем определяются аналогично показателям систем непрерывного времени и могут быть найдены с использованием тех же подходов при условии выполнения теоремы Котельникова-Шеннона для выбора интервала квантования Тпри переходе к дискретной форме описания системы.

Скорость протекания дискретных процессов определяется значениями модулей полюсов системы |z_i| = exp(-a_iT). Значения |z_i| уменьшаются с увеличением модулей вещественных частей полюсов непрерывной системы a_I, что равносильно увеличению быстродействия, т. е. уменьшению времени переходного процесса t_пп. Это служит основанием для введения (по аналогии с непрерывными системами) понятия степени устойчивости дискретной системы как радиуса распределения ее полюсов на комплексной плоскости.

Степенью устойчивости дискретной системы называется положительное число

h = max |z_i|, i = (1, n).

Cкорость протекания процессов возрастает при приближении полюсов к началу координат комплексной плоскости. Грубая оценка времени переходных процессов дискретной системы по степени устойчивости h (только по самой медленной составляющей переходного процесса) выполняется по формуле:

t_пп ≈ 3T/ln h.

литература

1. Мирошник И.В. Теория автоматического управления. Линейные системы: Учебное пособие для вузов. - СПб.: Питер, 2005. - 336 с.

2. Повзнер Л.Д. Теория систем управления: Учебное пособие для вузов. - М.: Изд. МГГУ, 2002. - 472 с.

4. Орлов А.И. Менеджмент: Учебник. – М.: "Изумруд", 2003. URL: http://www.aup.ru/books/m151/

11. Михайлов В.С. Теория управления. – К.: Выща школа, 1988.

12. Зайцев Г.Ф. Теория автоматического управления и регулирования. – К.: Выща школа, 1989.

Главный сайт автора ~ Лекции по ОТУ

О замеченных опечатках, ошибках и предложениях по дополнению: [e-mail].

Дата добавления: 2015-07-20