Оценка:__

Борисоглебск, 2011

Параллельный перенос

Цели:

Образовательные: познакомить учащихся с параллельным переносом и доказать, что параллельный перенос есть движение.

Развивающие: продолжатьразвивать математическую речь, внимание, самостоятельность, аккуратность при построении чертежей.

Воспитательные: прививать интерес к математике, а также формировать умение общаться, развивать навыки взаимопомощи, самоутверждения, самооценки.

Распределение урока по времени:

Содержание урока	Время
1. Организационный момент	3 минуты
2. Актуализация знаний	5 минут
3. Объяснение нового материала	20 минут
4. Закрепление изученного материала	12 минут

Ход урока.

I Актуализация знаний.

1. Проводится фронтальный опрос учащихся по вопросам:

· что такое отображение плоскости на себя? (Ответ: это сопоставление каждой точке плоскости какой-то точки этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке)

· что такое осевая симметрия? (Ответ: это отображение плоскости на себя относительно прямой, которое сохраняет расстояния между точками)

· что такое центральная симметрия? (Ответ: это отображение плоскости на себя относительно точки, которое сохраняет расстояния между точками)

· что такое движение плоскости? (Ответ: это отображение плоскости на себя, сохраняющее расстояния)

· является ли осевая симметрия движением? (Ответ: да)

II Объяснение нового материала.

На доске изображается отрезок MN и вектор . Учащимся объясняется алгоритм параллельного переноса, который они потом записывают к себе в тетрадь вместе с чертежом.

Расстояние между точками сохраняется. Поэтому параллельный перенос является движением.

Алгоритм параллельного переноса:

1. Из данных точек проводим прямые, параллельные данному вектору.

2. На каждой прямой откладываем отрезок, равный длине вектора в данном направлении.

3. Получаем точки, соответствующие данным.

Учащиеся записывают определение параллельного переноса: параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка M отображается в такую точку M₁, что вектор MM₁ равен вектору .

Учащийся вызывается к доске для решения примера.

Пример 1: даны векторы , и произвольный треугольник ABC, перенести произвольный треугольник ABC параллельным переносом относительно векторов , .

Делается вывод о том, что равные фигуры переходят в равные (т.к. сохраняется расстояние между точками). Учащиеся записывают это в тетрадь.

Затем вызывается к доске следующий учащийся для решения задачи:

№ 1164

Даны равнобедренный треугольник ABC с основанием AC и точка D на прямой AC, такая, что точка C лежит на отрезке AD.

а) Постройте отрезок B₁D, который получается из отрезка BC параллельным переносом на вектор CD.

б) Докажите, что четырехугольник ABB₁D – равнобедренная трапеция.

Дано: равнобедренный треугольник ABC, точка D.

Доказательство:

Т.к. ∆ABC – равнобедренный, то AB=BC, BC=B₁D (при параллельном переносе отрезки переходят в равные им отрезки), т.е. AB=B₁D.

Докажем теперь, что основания параллельны.

Они параллельны по построению BB₁ || CD, следовательно, BB₁ || AD.

Вывод: ABB₁D – равнобедренная трапеция.

III Закрепление изученного материала.

К доске вызывается следующий ученик для решения примера.

Пример 2: данную фигуру перенести параллельным переносом относительно векторов , .

Пример 3: дан ромб ABCD, перенести его параллельным переносом относительно вектора .

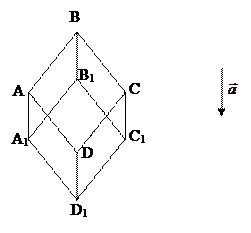
Дата добавления: 2015-07-20