
|
Читайте также: |
Синтез цепей возбуждения
На рис. 5.3 приведена обобщенная схема логической структуры синхронного счетчика. Из этой схемы понятен его принцип действия.

Рис. 5.3. Обобщенная схема логической структуры синхронного счетчика
Сигналы с выходов триггеров поступают на входы комбинационной схемы, которая преобразует поступившую информацию. Преобразованная информация не воспринимается триггерами до тех пор, пока на синхронизирующие входы триггеров не поступит считаемый сигнал. Сигналы, поступающие на входы триггеров, называют функциями возбуждения. Информация, находящаяся на входах каждого триггера, так сформирована комбинационной схемой, чтобы с приходом очередного считаемого сигнала осуществить переход счетчика из текущего состояния в следующее. Функции возбуждения i -го триггера можно записать в виде:

Значения всех переменных в этих выражениях определены для одного и того же момента времени t. Поэтому функции возбуждения переменных являются комбинационными (переключательными) функциями, которым соответствуют комбинационные схемы, формирующие входные сигналы для триггеров.
Следовательно, если задан тип триггера, то задача синтеза счетчика заключается в составлении функций возбуждения каждого триггера и минимизации найденных функций в заданном базисе.
Счетчики удобно синтезировать с помощью матриц переходов триггеров.
Закон функционирования любого триггера можно задать с помощью матрицы переходов. Число строк матрицы переходов для любого триггера равно четырем, что определяется числом возможных переходов из одного состояния в другое, а количество столбцов – числу логических входов триггера:
| Q(t) | Q(t+1) | E1 | E2 |
| 0 - | 
| 
| |
| 0 - |  
| 
| |
| 1 - | 
| 
| |
| 1 - | 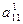
| 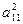
|
Элемент матрицы 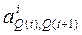 представляет собой значение входного сигнала Ei, под воздействием которого триггер переходит из состояния Q(t) в состояние Q(t+1). При этом каждый элемент матрицы может быть равен единице, нулю или являться неопределенным коэффициентом, если значение на входе не влияет на данный переход триггера.
представляет собой значение входного сигнала Ei, под воздействием которого триггер переходит из состояния Q(t) в состояние Q(t+1). При этом каждый элемент матрицы может быть равен единице, нулю или являться неопределенным коэффициентом, если значение на входе не влияет на данный переход триггера.
Матрицу переходов триггера составляют по таблице переходов этого триггера.
Матрица переходов J-K триггера
Из таблицы переходов J-K триггера найдем значения входных сигналов
J и K, которые вызывают переход триггера из состояния Q(t)=0 в состояние Q(t+1)=0. Ими являются следующие две пары сигналов: J=0, K=0; J=0, K=1. Из этого следует, что переменная J обязательно должна быть равна 0, а переменная K может принимать любое значение. Поэтому в столбце J первой строки запишем 0, а в столбце K значение b1. Рассуждая аналогичным образом, построим матрицу переходов J-K триггера:
| Q(t) | Q(t+1) | J | K |
| 0 - | b1 | ||
| 0 - | 1 
| b2 | |
| 1 - | b3 | ||
| 1 - | b4 |
Спроектируем суммирующий одноразрядный двоично-десятичный счетчик 8-4-2-1 на J-K триггерах. Состояния счетчика соответствуют таблице 5.1.
Таблица 5.1
| Десятичные цифры | Номер набора | Q3 | Q2 | Q1 | Q0 |
Функции возбуждения триггеров счетчика формируют с использованием кодированной таблицы переходов счетчика и матрицы переходов триггера. Для того чтобы получить кодированную таблицу переходов необходимо в одном столбце записать десять двоичных наборов, представляющих в данной системе кодирования все десятичные цифры. Эти состояния отнесем к моменту времени t и будем называть текущим состоянием счетчика. Текущие состояния записаны в колонках 1-4 табл. 5.2.
Затем в следующем столбце напротив каждого двоичного набора предыдущего столбца запишем новое состояние счетчика, в которое он перейдет после поступления считаемого сигнала. Данные состояния отнесем к моменту времени t+1 и будем называть следующим состоянием счетчика. Следующие состояния записаны в колонках 5-8 табл. 5.2.
Для составления функций возбуждения каждого J-K триггера воспользуемся его матрицей переходов.
Для минимизации функций возбуждения необходимо их представить в минимальной ДНФ. Для этого составим карты Карно для функций возбуждения. Для облегчения составления карт составим эталонную карту, где ячейки обозначим десятичными цифрами, соответствующими двоичным наборам конституенты единицы (рис. 5.4).

Рис.5.4. Эталонная карта Карно
Теперь составление карт Карно для функций возбуждения предельно упрощается. Занесем неопределенные значения ai в ячейки, цифровые обозначения которых совпадают с индексами рассматриваемых коэффициентов (рис. 5.5).

Рис. 5.5. Карты Карно для функций возбуждения J и K двоично-десятичного счетчика
Таблица 5.2
| Десятичные цифра | Номер набора | Значения выходов триггеров | Функции возбуждения триггеров | ||||||||||||||
| Текущее | Последующее | Текущее | |||||||||||||||
| Q3 | Q2 | Q1 | Q0 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 | ||
| a0 | a0 | a0 | a0 | ||||||||||||||
| a1 | a1 | a1 | a1 | ||||||||||||||
| a2 | a2 | a2 | a2 | ||||||||||||||
| a3 | a3 | a3 | a3 | ||||||||||||||
| a4 | a4 | a4 | a4 | ||||||||||||||
| a5 | a5 | a5 | a5 | ||||||||||||||
| a6 | a6 | a6 | a6 | ||||||||||||||
| a7 | a7 | a7 | a7 | ||||||||||||||
| a8 | a8 | a8 | a8 | ||||||||||||||
| a9 | a9 | a9 | a9 |
Дата добавления: 2015-07-20; просмотров: 225 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Счетчики | | | Синтез цепи переноса в следующие разряды |