
|
Читайте также: |
Условие теоремы: функция  непрерывна на отрезке
непрерывна на отрезке 
Заключение теоремы: справедлива формула 
Теорема сформулирована в условной форме.
Структура теоремы простая, т.к. посылка одна.
9. Теорема о количестве первообразных для заданных функций. Если  первообразная для функции
первообразная для функции  на промежутке
на промежутке  , то у функции
, то у функции  бесконечно много первообразных и все они имеют вид
бесконечно много первообразных и все они имеют вид 
Условие теоремы:  первообразная для функции
первообразная для функции  на промежутке
на промежутке  .
.
Заключение теоремы: у функции  бесконечно много первообразных и все они имеют вид
бесконечно много первообразных и все они имеют вид 
Теорема сформулирована в условной форме.
Структура теоремы простая, т.к. посылка одна.
10. Формула вычисления площади криволинейной трапеции. 
11. Понятие криволинейной трапеции. В декартовой прямоугольной системе координат дана фигура ограниченная осью 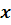 , прямыми
, прямыми  (
(  ) и графиком непрерывной и неотрицательной на отрезке
) и графиком непрерывной и неотрицательной на отрезке 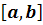 функции
функции  ; назовём такую фигуру криволинейной трапецией.
; назовём такую фигуру криволинейной трапецией.
Объёмом понятия являются все фигуры.
Существенный признак: фигура ограниченная осью  , прямыми
, прямыми 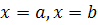 (
( ) и графиком непрерывной и неотрицательной на отрезке
) и графиком непрерывной и неотрицательной на отрезке  функции
функции  .
.
Структура определения: конъюнктивная.
Способ определения: через ближайший род и видовые отличия.
12. Правило нахождения площади плоских фигур с помощью определённого интеграла. Площадь  фигуры, ограниченной прямыми
фигуры, ограниченной прямыми 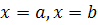 и графиками функций
и графиками функций 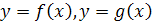 , непрерывных на отрезке
, непрерывных на отрезке  и таких, что для всех
и таких, что для всех  из отрезка
из отрезка  выполняется неравенство
выполняется неравенство  , вычисляется по формуле
, вычисляется по формуле

13. Понятие процесса дифференцирования. Процесс отыскания производной по заданной функции называют дифференцированием.
Объёмом понятия являются все процессы.
Существенный признак: процесс отыскания производной по заданной функции.
Структура определения: конъюнктивная.
Способ определения: через ближайший род и видовые отличия.
14. Понятие процесса интегрирования. Процесс отыскания функции по заданной производной называют интегрированием.
Объёмом понятия являются все процессы.
Существенный признак: процесс отыскания функции по заданной производной.
Структура определения: конъюнктивная.
Способ определения: через ближайший род и видовые отличия.
Дата добавления: 2015-07-20; просмотров: 65 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Раздел 2. Новые математические факты данной темы. | | | Тема: первообразная и неопределённый интеграл (3 часа). |