Построение гидравлических характеристик трубопровода.

Для построения характеристики трубопровода, т.е. зависимости потребного напора Н_потр от расхода жидкости Q_р, определяется величина приведённой высоты нагнетания ΔΖ' суммарных потерь напора h на трение жидкости о стенки трубопровода h_тр потерь напора на местных сопротивлениях h_м:

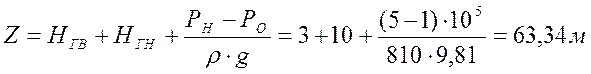
Определяем скорость движения жидкости для 7 режимов расхода жидкости:

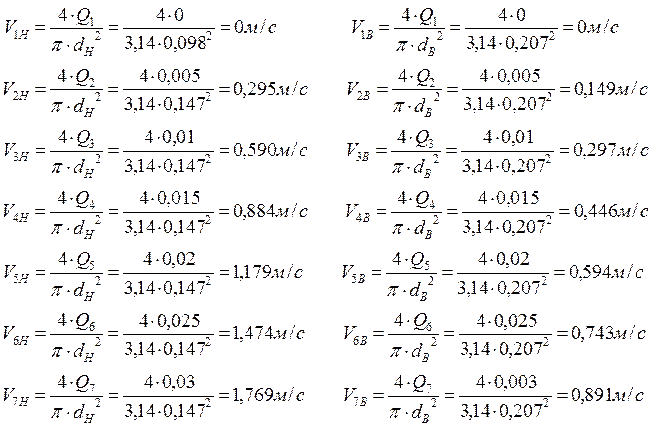и относительный эквивалент шероховатости внутренней поверхности труб:

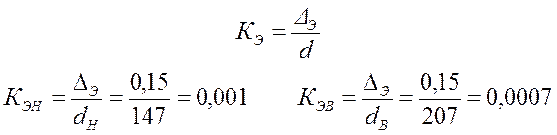
Определяем число Рейнольдса:

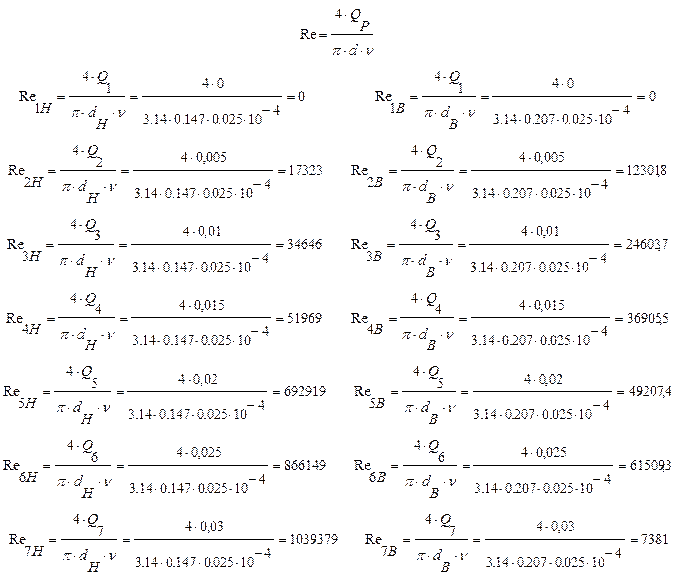
Исходя из числа Рейнольдса определяем коэффициент Дарси λ:

Для ламинарного режима при Re ≤ Re_кр =2320 коэффициент Дарси рассчитывается по формуле Стокса:

Для турбулентного режима течения жидкости коэффициент Дарси рассчитывается по эмпирическим и полуэмпирическим формулам:

в зоне гладкого трения Re_кр < Re ≤ Re'₁= 15/К_Э

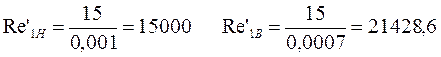
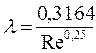
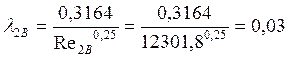
в зоне смешанного трения Re'₁ < Re ≤ Re'₂ = 580/К_Э

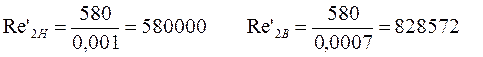
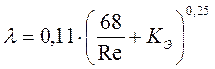–– формула Альтшуля

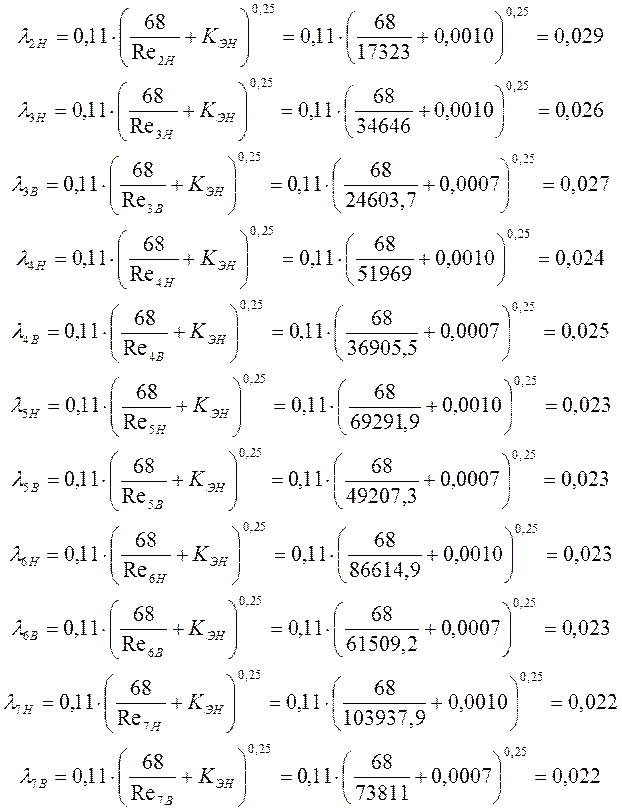
Потери на трение определяются по формуле Дарси – Вейсбаха:

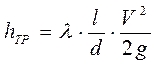
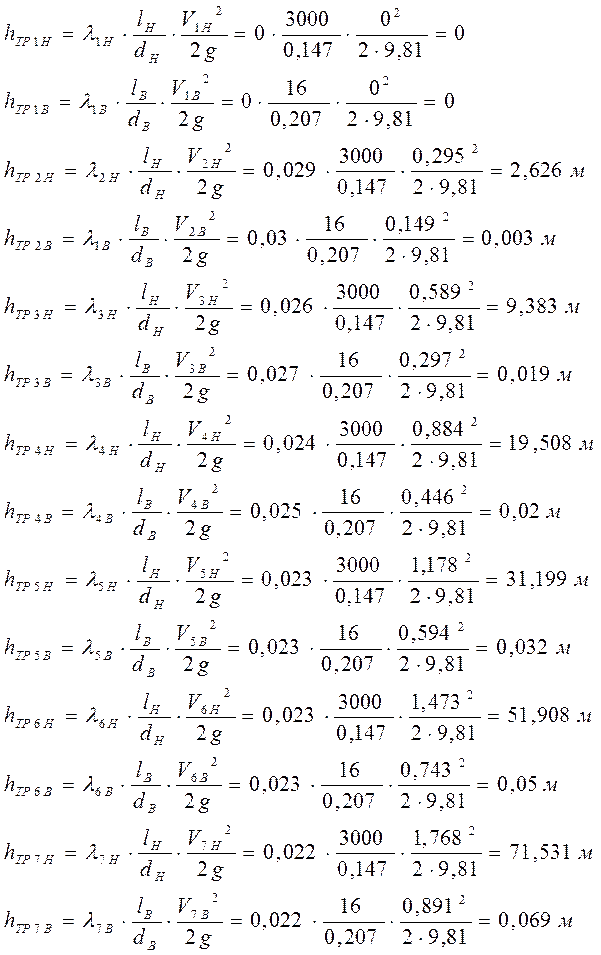
Потери на местных сопротивлениях вычисляются по формуле:

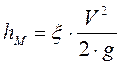
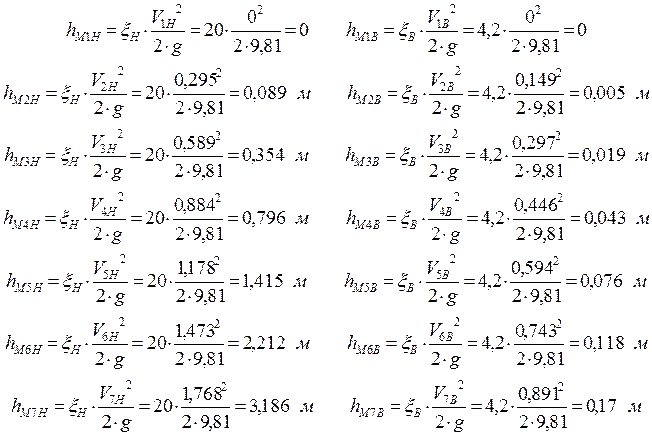
Суммарные потери напора h определяем по формуле:

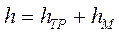
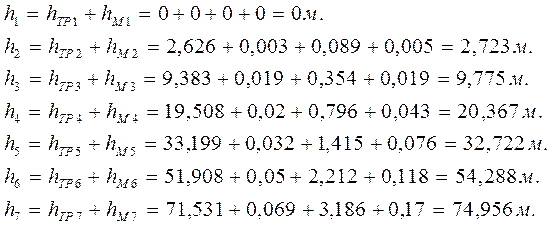
Потребный напор определяем сложением суммарных потерь напора h и приведённой высоты нагнетания Ζ:

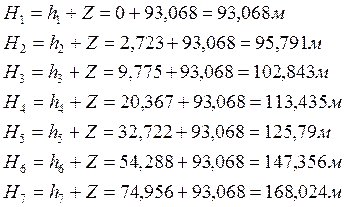
Таблица 1. Результаты гидравлического расчёта трубопровода.

Q , м /ч	V, м/с	Re	λ	H , м	H , м	h, м	Z, м	H, м
0∙Q =0	В   Н							93,068	93,068
0,2∙Q =18	В   Н	0,149   0,295		0,03   0,029	0,003   2,626	0,0035   0,0709	2,723	95,791
0,4∙Q =36	В   Н	0,297   0,589		0,027   0,026	0,019   9,383	0,0139   0,2834	9,775	102,843
0,6∙Q =54	В   Н	0,446   0,884		0,025   0,024	0,02   19,508	0,0313   0,6377	20,367	113,435
0,8∙Q =72	В   Н	0,594   1,178		0,023   0,023	0,032   33,199	0,0557   1,1336	32,722	125,79
1,0∙Q =90	В   Н	0,743   1,473		0,023   0,023	0,05   51,908	0,0870   1,7713	54,288	147,356
1,2∙Q =108	В   Н	0,891   1,768		0,022   0,022	0,069   71,531	0,1253   2,5507	74,956	168,024

Дата добавления: 2015-07-20