
Читайте также:
|
На основе данных группировки определяют (задача 2) среднюю величину признака (
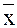 ), дисперсию (
), дисперсию (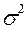 ) и среднее квадратическое отклонение (
) и среднее квадратическое отклонение (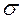 ), применяя способ «моментов», а также коэффициент вариации (
), применяя способ «моментов», а также коэффициент вариации (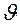 )по следующим формулам:
)по следующим формулам:
 , где
, где 
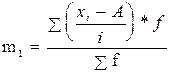
 (1.2)
(1.2)
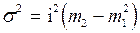 , где
, где 
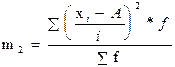
 (1.3)
(1.3)
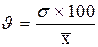
где х i - среднее значение признака в каждой группе;
f - частоты;
А - постоянное число. В рядах распределения с равными интервалами за постоянное число принято брать варианту с наибольшей частотой, т. е. модальную варианту.
При этом следует иметь в виду, что для расчета этих показателей интервальный ряд распределения преобразовывают в дискретный путем определения середины интервала. В нашем примере середина первого интервала –6,5.
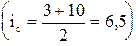 , второго – 13,5
, второго – 13,5 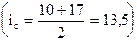 и т.д.
и т.д.
При построении гистограммы распределения на оси абсцисс откладывают интервальные значения признака, строят прямоугольники, высота которых равна величине частот, откладываемых на оси ординат.
Дата добавления: 2015-07-20; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача 4 | | | Тема:Ряды динамики. |