Маршрутизация массовых крупнопартионных перевозок

Цель: определить оптимальные маршруты при перевозке массовых грузов большими партиями (помашинными отправками).

Одной из основных задач, выполняемых при оперативном планировании перевозок массовых крупнопартионных грузов, является оптимизация их маршрутов с целью повышения коэффициента использования пробега.

Пусть груз, сосредоточенный в пунктах А ₁, А ₂ ,..., А_i,..., А_m в количествах соответственно а ₁, а ₂ ,..., а_i,..., а_m, необходимо доставить в пункты В ₁, В ₂ ,..., В_j,..., В_n в количествах b ₁, b ₂ ,..., b_j,..., b_n тонн. Объем перевозок из i -го пункта отправления в j -й пункт назначения составляет P_ij тонн. Будем полагать, что для перевозок используют условные однотонные (q g = 1 т) автомобили.

При выполнении перевозок в пункт В_j доставляют

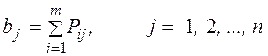
тонн груза и соответственно прибывает такое же количество условных автомобилей, которые после разгрузки подают в пункты погрузки А_i. Так как из пунктов А_i нужно вывезти

тонн груза, то для пунктов А ₁, А ₂ ,..., А_i,..., А_m необходимо осуществить соответственно а ₁, а ₂ ,..., а_i,..., а_m подач порожних автомобилей.

Расстояния (l_ji = l_ij) от каждого потребителя В_j до каждого поставщика А_i известны.

Требуется определить количество x_ji подач порожних условных однотонных автомобилей от j -го пункта разгрузки в i -й пункт погрузки, с тем чтобы общий пробег автомобилей был минимальным. Иными словами, задача сводится к нахождению оптимального плана возврата (подач) порожних автомобилей.

Порожний пробег при выполнении из j -го в i -й пункт x_ji подач условных однотонных автомобилей равен l_jix_ji. Тогда их суммарный пробег:

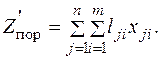
Поскольку количество ездок равно x_ji/q g_ст, то фактический пробег автомобиля с заданной грузоподъемностью q равен

Математическая формулировка задачи определяется следующим образом. Требуется определить совокупность величин 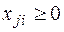(план возврата порожних автомобилей), удовлетворяющих условиям

(1.1)

(1.2)

и минимизирующих функцию

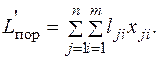(1.3)

Поскольку количество завозимых грузов равно количеству вывозимых, то справедливо равенство

(1.4)

Данная задача представляет собой классическую задачу линейного программирования. Рассмотрим методику ее решения на примере.

Заявки на перевозки, включенные в план автотранспортного предприятия, перечислены в табл. 1.1. На основании заявок на перевозки составлена матрица (табл. 1.2), в которой указаны количества тонн грузов, вывозимых из каждого пункта А_i (i = 1,2,3,4) и завозимых в каждый пункт В_j (j = 1,2,3,4,5,6,7), а также расстояния между этими пунктами (они представлены в верхнем правом углу соответствующих клеток).

Данная задача нахождения оптимального возврата порожних автомобилей (условных автотонн), записанная в матричной форме, решается как обычная транспортная задача методом потенциалов.

В матрицу (табл. 1.3) заносятся грузоотправители, грузополучатели, расстояния между ними, данные наличия порожних автомобилей и потребители. Последовательность вычислений при составлении оптимального плана показана на схеме (рис. 1).

Для дальнейшего решения задачи необходимо составить план возврата порожних автомобилей. При этом должны соблюдаться некоторые условия:

m + n – 1 = N, (1.5)

где m – количество строк и n – количество столбцов в матрице; N – количество загруженных клеток в матрице.

Для нашего примера N =10, так как m =7 и n =4 и 7 + 4 – 1 = 10.

Таблица 1.1

Заявки на перевозки

Отправитель	Получатель	Род груза	Объем завоза, т
Угольный склад (А 1)	Речной порт (В 1) Мастерские (В 2) Школа (В 3)	Уголь
Песчаный карьер (А 2)	Речной порт (В 1) Набережная (В 4)	Песок
Товарная станция (А 3)	Завод ЖБК (В 6) Автовокзал (В 7)	Гравий
Карьер (А 4)	Мастерские (В 2) Запас (В 5) Автовокзал (В 7)	Щебень

Таблица 1.2

План-заявка на перевозку грузов

(матричная форма)

Грузополучатель	Грузоотправитель	Завоз, т
А1	А2	А3	А4
В1	85 ^1,90	42 ^1,85	^3,35	^3,04
В2	36 ^6,66	^10,01	^8,09	28 ^7,78
В3	41 ^1,22	^2,53	^2,67	^2,36
В4	^8,86	13 ^12,21	^10,29	^9,98
В5	^4,14	^7,06	^3,31	24 ^3,00
В6	^3,44	^5,81	48 ^5,69	^5,38
В7	^6,56	^8,83	23 ^8,52	18 ^8,21
Вывоз, т

Расчет индексов:

1. Для занятых клеток матрицы должно соблюдаться следующее условие:

U_i + V_j = L_ij, (1.6)

где L_ij – расстояние между грузоотправителем и грузополучателем.

Составление матрицы

Построение допустимого исходного плана

Подсчет количества занятых клеток матрицы (N) и сравнение его с числом m + n – 1

N < m + n – 1

N = m + n – 1

N > m + n – 1

Заполнение недостающих клеток путем фиктивной загрузки

Ликвидация лишних заня­тых клеток

Расчет индексов

Проверка незанятых клеток матрицы с целью отыскания по­тенциальных

Потенциальных клеток нет

Потенциальные клетки есть

Построение замкнутой цепочки возможных перемещений для клетки с наибольшим потенциалом

Расстановка знаков «+» и «–» по вершинам цепочки

Отыскание среди загрузок со знаком «–» наименьшей по вели­чине

Изменение на эту величину загрузок на вершинах контура

Решение закончено: оптимальный план возврата порожних автомобилей составлен

  Рис. 1. Блок‑схема последовательности вычислений

2. Для свободных клеток:

U_i + V_j £ L_ij. (1.7)

В случае если данное неравенство не выполняется, то вычисляется потенциал:

d = U_i + V_j - L_ij. (1.8)

Коэффициенты U_i и V_j рассчитывают следующим образом: напротив любой загруженной клетки в дополнительным строке или столбце записывают коэффициент 0 (например для потребителя B1 V₁ =0).
Далее, двигаясь по цепочке загруженных клеток, по условию (1.6) находят все остальные коэффициенты. Например, коэффициент при
A1 U₁ =1,9-0=1,9; при B2 V₂ =6,66-U₁ =6,66-1,9=4,76; при A4
U₄ = 7,78-V₂ =7,78-4,76=3,02 и т.д. Результаты заносят в табл. 1.4.

Таблица 1.3

Матрица

Грузополучатель	Грузоотправитель	Завоз, т
А1	А2	А3	А4
В1	85 ^1,90	42 ^1,85	^3,35	^3,04
В2	36 ^6,66	^10,01	^8,09	28 ^7,78
В3	41^1,22	^2,53	^2,67	^2,36
В4	^8,86	13 ^12,21	^10,29	^9,98
В5	^4,14	^7,06	^3,31	24 ^3,00
В6	^3,44	^5,81	48 ^5,69	^5,38
В7	^6,56	^8,83	23 ^8,52	18 ^8,21
Вывоз, т

Таблица 1.4

План возврата порожних автомобилей

Грузополучатель	Коэффициенты Vj	Грузоотправитель
А1	А2	А3	А4
Коэффициенты Ui
1,9	1,85	3,33	3,02
В1		85 ^1,90	42 ^1,85	^3,35	^3,04
В2	4,76	36 ^6,66	^10,01	^8,09	28 ^7,78
В3	-0,68	41 ^1,22	^2,53	^2,67	^2,36
В4	10,36	^3.4 ´ ^8,86	13 ^12,21	^3.4 ´ ^10,29	^3.4 ´ ^9,98
В5	-0,02	^4,14	^7,06	^3,31	24 ^3,00
В6	2,36	^0.82 ´ ^3,44	^5,81	48 ^5,69	^5,38
В7	5,19	^0.53 ´ ^6,56	^8,83	23 ^8,52	18 ^8,21

Затем проверяют свободные (незагруженные) клетки матрицы на потенциальность по условию (1.7). Если условие (1.7) нарушается, клетки помечают знаком ´ и вычисляют потенциал по условию (1.8), и значение потенциала помещают в левый верхний угол клетки.

В табл. 1.4 в результате расчетов получилось пять потенциальных клеток. Выбирают клетку с максимальным потенциалом (A1 B4) и составляют контур пересчета. Согласно алгоритму (рис. 1) расставляют знаки «+» и «–» по вершинам контура и среди клеток со знаком «–» выбирают минимальное число. В нашем примере min=13 (клетка A2 B4).

На минимальную загрузку (13) делают перераспределение по вершинам контура (в клетки со знаком «+» прибавляют 13, а из клеток со знаком «–» отнимают 13). После перераспределения объемов новые значения (в скобках) заносят в новую матрицу (табл. 1.5).

Таблица 1.5

План возврата порожних автомобилей

Грузополучатель	Коэффициенты Vj	Грузоотправитель
А1	А2	А3	А4
Коэффициенты Ui
1,9	1,85	3,33	3,02
В1		72 ^1,90	55 ^1,85	^3,35	^3,04
В2	4,76	36 ^6,66	^10,01	^8,09	28 ^7,78
В3	-0,68	41 ^1,22	^2,53	^2,67	^2,36
В4	6,96	13 ^8,86	^12,21	^10,29	^9,98
В5	-0,02	^4,14	^7,06	^3,31	24 ^3,00
В6	2,36	^0.82 ´ ^3,44	^5,81	48 ^5,69	^5,38
В7	5,19	^0.53 ´ ^6,56	^8,83	23 ^8,52	18 ^8,21

Процесс построения оптимального плана повторяют заново: находят коэффициенты по условию (1.6), проверяют свободные клетки на потенциальность по условию (1.7), и если они есть, то рассчитывают потенциалы и строят контур перечета. Процесс построения оптимального плана считается законченным, если в матрице нет больше потенциальных клеток.

Последующие этапы решения задачи представлены в табл. 1.6-1.9.

Таблица 1.6

План возврата порожних автомобилей

Грузополучатель	Коэффициенты   Vj	Грузоотправитель
А1	А2	А3	А4
Коэффициенты Ui
1,9	1,85	4,15	3,02
В1		72 ^1,90	55 ^1,85	^0,8 ´ ^3,35	^3,04
В2	4,76	18 ^6,66	^10,01	^0,8^2 ´ ^8,09	46 ^7,78
В3	-0,68	41 ^1,22	^2,53	^0,8 ´ ^2,67	^2,36
В4	6,96	13 ^8,86	^12,21	^0,82 ´ ^10,29	^9,98
В5	-0,02	^4,14	^7,06	^0,82 ´ ^3,31	24 ^3,00
В6	1,54	18 ^3,44	^5,81	30 ^5,69	^5,38
В7	4,37	^6,56	^8,83	41 ^8,52	^8,21

В результате решения получаем оптимальный план возврата порожних автомобилей (в матрице нет больше потенциальных клеток) (табл. 1.10). Полученный оптимальный план совмещают с планом-заявкой на перевозку грузов (см. табл. 1.2), получая в результате совмещенный план (табл. 1.11).

Таблица 1.7

План возврата порожних автомобилей

Грузополучатель	Коэффициенты Vj	Грузоотправитель
А1	А2	А3	А4
Коэффициент Ui
1,9	1,85	4,15	3,84
В1		72 ^1,90	55 ^1,85	^0,8 ´ ^3,35	^0,8 ´ ^3,04
В2	3,94	^6,66	^10,01	18 ^8,09	46 ^7,78
В3	-0,68	41 ^1,22	^2,53	^0,8 ´ ^2,67	^0,8 ´ ^2,36
В4	6,96	13 ^8,86	^12,21	^0,82 ´ ^10,29	^0,82 ´ ^9,98
В5	-0,02	^4,14	^7,06	^0,82 ´ ^3,31	24 ^3,00
В6	1,54	36 ^3,44	^5,81	12 ^5,69	^5,38
В7	4,37	^6,56	^8,83	41 ^8,52	^8,21

Таблица 1.8

План возврата порожних автомобилей

Грузополучатель	Коэффициенты Vj	Грузоотправитель
А1	А2	А3	А4
Ui
1,9	1,85	3,33	3,02
В1		72 ^1,90	55 ^1,85	^3,35	^3,04
В2	4,76	^6,66	^10,01	30 ^8,09	34 ^7,78
В3	-0,68	41 ^1,22	^2,53	^2,67	^2,36
В4	6,96	1 ^8,86	^12,21	^10,29	12 ^9,98
В5	-0,02	^4,14	^7,06	^3,31	24 ^3,00
В6	1,54	48 ^3,44	^5,81	^5,69	^5,38
В7	5,19	^0,53 ´ ^6,56	^8,83	41 ^8,52	^8,21

Цифры в скобках обозначают груженые ездки, цифры без скобок - порожние ездки. Из совмещенного плана выбирают маршруты перевозок грузов в такой последовательности: маятниковые, кольцевые 4-, 6- угольные и пр.

Таблица 1.9

План возврата порожних автомобилей

Грузополу-чатель	Коэффициенты Vj	Грузоотправитель
А1	А2	А3	А4
Коэффициенты Ui
1,9	1,85	3,86	3,55
В1		72 ^1,90	55 ^1,85	^0,51 ´ ^3,35	^0,51 ´ ^3,04
В2	4,23	^6,66	^10,01	31 ^8,09	33 ^7,78
В3	-0,68	41 ^1,22	^2,53	^0,51 ´ ^2,67	^0,51 ´ ^2,36
В4	6,43	^8,86	^12,21	^10,29	13 ^9,98
В5	-0,55	^4,14	^7,06	^3,31	24 ^3,00
В6	1,54	48 ^3,44	^5,81	^5,69	^5,38
В7	4,66	1 ^6,56	^8,83	40 ^8,52	^8,21

Таблица 1.10

Оптимальный план возврата порожних автомобилей

Грузополу- чатель	Грузоотправитель	Коэффициент
А1	А2	А3	А4
В1	32 ^1,90	55 ^1,85	40 ^3,35	^3,04
В2	^6,66	^10,01	31 ^8,09	33 ^7,78	4,74
В3	41 ^1,22	^2,53	^2,67	^2,36	-0,68
В4	^8,86	^12,21	^10,29	13 ^9,98	6,94
В5	^4,14	^7,06	^3,31	24 ^3,00	-0,04
В6	48 ^3,44	^5,81	^5,69	^5,38	1,54
В7	41 ^6,56	^8,83	^8,52	^8,21	4,66
Коэффициент	1,9	1,85	3,35	3,04

Таблица 1.11

Совмещенный план

Грузополучатель	Грузоотправитель	Коэффициент
А1	А2	А3	А4
В1	32 ^1,90 (85)	55 ^1,85 (42)	40 ^3,35	^3,04
В2	^6,66 (36)	^10,01	31 ^8,09	33 ^7,78 (28)	4,74
В3	41 ^1,22 (41)	^2,53	^2,67	^2,36	-0,68
В4	^8,86	^12,21 (13)	^10,29	13 ^9,98	6,94
В5	^4,14	^7,06	^3,31	24 ^3,00 (24)	-0,04
В6	48 ^3,44	^5,81	^5,69 (48)	^5,38	1,54
В7	41 ^6,56	^8,83	^8,52 (23)	^8,21 (18)	4,66
Коэффициент	1,9	1,85	3,35	3,04

Количество тонн грузов, перевозимых на каждом маятниковом маршруте, определяется меньшей из двух цифр в соответствующих клетках, указывающих объем завоза и потребность в порожних автомо­билях:

Маршрут Объем перевозок, т

А₁ – В₃ – А₁ 41

А₄ – В₅ – А₄ 24

А₁ – В₁ – А₁ 32

А₂ – В₁ – А₂ 42

А₄ – В₂ – А₄ 28

Запланированные на маятниковых маршрутах перевозки (завоз грузов и возврат порожних автомобилей) исключают из матрицы и про­должают составление маршрутов. Когда все маятниковые маршруты найдены, в матрице строят замкнутый контур, все вершины которого лежат в «загруженных» клетках. Вершины, находящиеся в клетках, где стоят цифры, обозначающие груженые ездки, должны чередоваться с вершинами в клетках, где есть цифры, указывающие на количество порожних ездок.

В нашем случае такому контуру соответствует маршрут

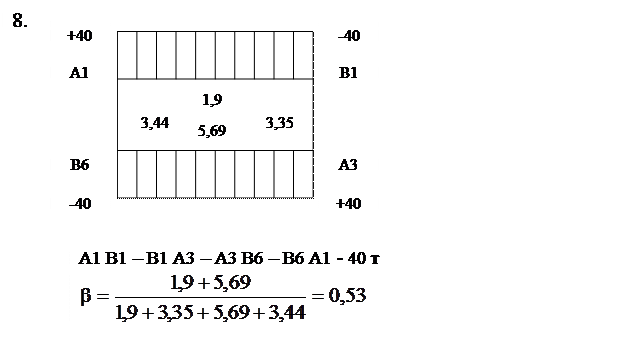
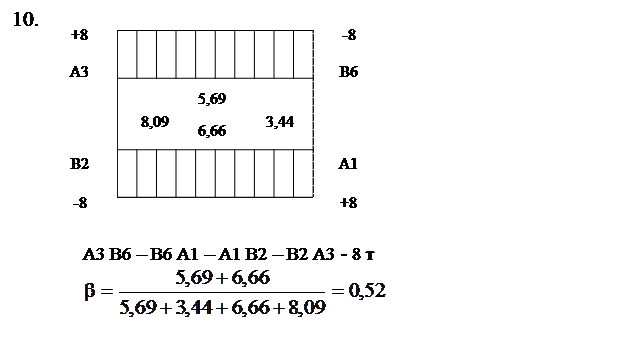
А₁ В₁ – В₁ А₂ – А₂ В₄ – В₄ А₄ – А₄ В₇ – В₇ А₁.

На нем каждому потребителю должно быть завезено 13 т грузов, так как минимальное значение загрузок по вершинам контура составляет именно 13. Уменьшив цифры в клетках, составляющих выбранный маршрут, на 13 единиц, получим данные для выбора второго кольцевого маршрута. Процесс составления маршрутов считается законченным, когда в матрице не остается ни одной загрузки.

Для каждого маршрута необходимо определить коэффициент использования пробега. Если на кольцевом маршруте коэффициент использования пробега b = 0,5, то такой маршрут не целесообразен, соответствующие перевозки лучше осуществлять на маятниковых маршрутах.

Дата добавления: 2015-07-20