Степень подвижности кинематической цепи

Число степеней свободы кинематической цепи относительно одного из её звеньев называют степенью её подвижности.

Для определения степени подвижности W цепи необходимо из общего числа степеней свободы её подвижных звеньев вычесть число связей, ограничивающих относительное движение звеньев кинематическими парами, которые связывают звенья.

Если n – число подвижных звеньев цепи, а P_i – число кинематических пар i -го класса, то 6n – число степеней свободы подвижных звеньев механизма, iP_i – общее число связей, наложенных на звенья механизма кинематическими парами i -го класса.

В соответствии со сказанным степень подвижности кинематической цепи

Для пространственной кинематической цепи общего вида формула (1.1) принимает вид формулы Сомова – Малышева

При пользовании формулой (1.2) необходимо учитывать ограничения, накладываемые на движение всех звеньев кинематической цепи.

Например, для плоской кинематической цепи, у которой звенья движутся параллельно одной неподвижной плоскости, перпендикулярной осям вращательных пар, число наложенных общих связей равно трём. Звенья такой цепи не могут перемещаться в направлении оси, перпендикулярной к неподвижной плоскости и вращаться относительно 2^х осей, лежащих в этой плоскости. Число степеней свободы каждого звена уменьшается здесь на 3 – число общих связей.

Общее число степеней свободы n звеньев цепи будет равно (6-3)n, а каждая кинематическая пара в этом случае накладывает на движение звеньев цепи на 3 ограничения меньше класса пары. Поэтому пары 5 и 4 класса накладывают на движение звеньев цепи соответственно два и одно ограничения, а кинематические пары 3,2 и 1^го класса не имеет места в рассматриваемой цепи.

Для плоской кинематической цепи формула 1.2 принимает вид формулы Чебышева

Кинематические пары 5 класса могут присутствовать в плоском механизме в виде вращательных и поступательных пар.

Определив по формулам (1.2) или (1.3) с учётом общих связей степень подвижности кинематической цепи механизма, мы тем самым находим необходимое число независимых между собой координат (обобщённых координат), которое необходимо для однозначной определённости положений всех звеньев механизма.

В частности, для механизма шарнирного четырёхзвенника имеем (рис. 1.2):

n = 3, P₅ = 4; P_y = 0.

По формуле (1.3) получим

Естественно, что данный механизм должен иметь одно ведущее звено и одну обобщённую координату, в качестве которой обычно выбирают угловую координату ведущего звена f₁.

Для кривошипно-ползунного механизма (рис 1.5) параметры формулы (1.3) такие же, как и для шарнирного четырёхзвенника. Ведущее звено (ползун) движется прямолинейно и за обобщенную координату принимается линейная координата S ползуна.

В механизмах с двумя степенями подвижности выбираются в качестве обобщённых координат координаты 2^х ведущих звеньев или одного звена, если оно образует со стойкой кинематическую пару с 2^мя степенями свободы.

Формула (1.2) несправедлива для механизмов с избыточными (пассивными) связями. Избыточными связями в механизме называют повторяющиеся связи, которые дублируют ограничения, наложенные другими связями, и поэтому они могут быть удалены из механизма без изменения заданного числа его степеней свободы. Если число избыточных связей обозначить q, то степень подвижности механизма с избыточными связями определяется из равенства:

В плоском шарнирном -звеннике (Рис.1.2) W=1,n=3,P₅=4. Число избыточных связей находится по формуле (1.4)

Устранены избыточные связи в механизме могут быть изменением подвижности некоторых кинематических пар.

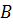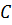В частности, если в рассмотренном плоском шарнирном -звеннике вращательную пару заменить на сферическую пару класса , а вращательную пару –на сферическую с пальцем пару 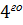класса 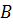, то полученный таким образом механизм пространственного -звенника (Рис.1.4) будет иметь: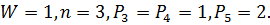

Тогда

Таким образом в механизме пространственного -звенника избыточные связи отсутствуют.

Дата добавления: 2015-07-20