Пример выполнения индивидуального задания

Исходные данные:

1-е звено	X 1 = 2 X
2-е звено	pX 3 + 2 x 3 = x 2
Звено МОС	pX 4 + X 4 = 2 рX 3
3-е звено	2 p ^2 У +2 pУ + У = 2 X 3
Звено ГОС	2 У 1 = У

Рис.1.64. Схема автоматической системы регулирования

1. Определение передаточных функций звеньев.

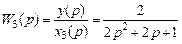
2. Определение передаточных функций системы по управляющему воздействию.

Передаточная функция замкнутой CAP по управляющему воздействию определяет взаимосвязь между изменением регулируемой величины У и изменением задающего воздействия G:

,

где W _п(p) – передаточная функция прямой цепи системы;

W _р(p) – передаточная функция разомкнутой системы;

W _ос(р) – передаточная функция обратной связи системы.

Обычно мысленно размыкают главную обратную связь перед сравнивающим устройством. На рис. 1.64 место размыкания показано волнистой чертой в точке А.

Перед нахождением передаточных функций систему необходимо привести к одноконтурной, избавившись от перекрестных связей и заменив звенья, охваченные местными обратными связями и соединенные параллельно, на эквивалентные.

Предварительно заменим звено, охваченное местной обратной связью (МОС) (рис. 1.64), одним эквивалентным звеном. Передаточная функция звена или цепи, последовательно соединенных звеньев, охваченных обратной связью, определяется по формуле:

,

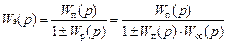где W _п(p) – передаточная функция прямой цепи;

W _р(р) – передаточная функция разомкнутой цепи;

W _ос(р) – передаточная функция обратной связи;

знак «+» в знаменателе соответствует отрицательной обратной связи;

знак «–» – соответствует положительной обратной связи.

В нашем случае:

Передаточную функцию прямой цепи W _п(p) системы найдем по формуле:

Передаточную функцию разомкнутой системы W _р(p) системы найдем по формуле:

;

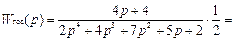
Для рассматриваемого примера передаточная функция замкнутой CAP по управляющему воздействию G:

Примечание.

Для системы без местной обратной связи приводить систему к одноконтурной нет необходимости, поскольку она уже является таковой.

3. Анализ устойчивости системы.

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после снятия воздействия, вызвавшего выход из установившегося режима.

Выходная величина устойчивой системы остается ограниченной в условиях действия на систему ограниченных по величине воздействий.

Неустойчивая система является неработоспособной, поэтому проверка устойчивости является обязательным этапом анализа системы.

Условием устойчивости линейной системы является отрицательность действительной части корней характеристического уравнения системы. При нулевых корнях система находится на границе устойчивости. Поскольку решение уравнений высокого порядка сопряжено с определенными трудностями, то анализ устойчивости линейных систем проводится по алгебраическим и частотным критериям. Наиболее часто используют алгебраический критерий Гурвица и частотные критерии Михайлова и Найквиста.

4. Анализ устойчивости по критерию Гурвица.

Передаточная функция линейной CAP в общем случае имеет вид:

.

Полином Q (p), находящийся в знаменателе передаточной функции, называется характеристическим полиномом системы, поскольку он определяет характер свободного движения системы. Уравнение Q (p) = 0 называется характеристическим уравнением системы.

Устойчивость по критерию Гурвица проверяется следующим образом. Из коэффициентов характеристического уравнения:

Q(р) = а ₀ рⁿ + а ₁ р^{n– 1} + … + a_{n– 1} p + a_n = 0

составляется определитель Гурвица по следующему правилу. По главной диагонали последовательно записываются n коэффициентов характеристического уравнения, начиная с a ₁. Сверху от элементов главной диагонали в каждом столбце записываются коэффициенты характеристического уравнения с последовательно возрастающими, а снизу с последовательно убывающими индексами. На месте коэффициентов с индексами большими n или меньшими 0 записываются нули. Полученный определитель содержит n строк и n столбцов:

Далее составляются диагональные миноры определителя Гурвица:

∆₁ = а ₁;

;

и т. д.

Критерий Гурвица формулируется следующим образом.

Для устойчивости линейной системы необходимо и достаточно, чтобы при а ₀ > 0 все диагональные миноры определителя Гурвица были положительными.

Для характеристических уравнений первой и второй степеней условия устойчивости сводятся к требованию положительности всех коэффициентов.

Для уравнений третьей и четвертой степеней, помимо положительности всех коэффициентов характеристического уравнения, необходима положительность определителя ∆ _{n –1}.

Поэтому условия устойчивости, для систем с характеристическим уравнением третьей степени:

а ₀ > 0; a ₁ > 0; а ₂ > 0; а ₃ > 0;

∆₂ = a ₁ а ₂ – а ₃ а ₀ > 0.

Условия устойчивости для систем с характеристическим уравнением четвертой степени:

а ₀ > 0; a ₁ > 0; а ₂ > 0; а ₃ > 0; а ₄ > 0;

∆₃ = а ₃ (a ₁ а ₂ – а ₃ а ₀) – а ₄ а ₁² > 0.

Определим устойчивость CAP для нашего случая. Для этого можно воспользоваться любой из полученных ранее передаточных функций системы, из которых следует, что характеристическое уравнение системы:

Q (p) = 2 р ⁴ + 4 р ³ + 7 р ² + 7 р + 4 = 0.

Для анализа устойчивости воспользуемся основными условиями устойчивости. Так как a ₀ = 2 > 0, найдем значения диагональных миноров. Составим определитель Гурвица:

Определим значения диагональных миноров:

D₁ = 4 > 0;

;

;

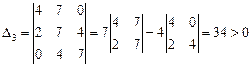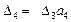= 4 × 34 = 136 > 0.

Полученный результат показывает, что система устойчива.

5. Анализ устойчивости по критерию Михайлова.

Этот критерий устойчивости был предложен советским ученым А. В. Михайловым и позволяет судить об устойчивости замкнутой системы на основании рассмотрения некоторой кривой.

Кривая Михайлова представляет собой годограф вектора (характеристический полином):

М (jw) = a ₀(jw) ⁿ + a ₁(jw) ^{n– 1} + …+ a_{n– 1}(jw) + a_n,

получаемый из характеристического уравнения системы путем подстановки р = jw.

Выделив в правой части последнего уравнения вещественную U (w) и мнимую V (w) части, можно записать:

М (jw) = U (w) + jV (w).

Формулировка критерия Михайлова сводится к следующему: чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая Михайлова при изменении частоты w от 0 до ¥, начинаясь при w = 0 на вещественной положительной полуоси, обходила только против часовой стрелки последовательно п квадрантов, уходя в бесконечность в последнем квадранте, где п – порядок характеристического уравнения.

Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов плоскости [ U; jV ].

Определим устойчивость CAP для нашего случая.

В характеристическом уравнении для замкнутой АС вместо оператора p подставим значение (jw) и получим:

М(jw) = 2(jw)⁴ + 4(jw)³ + 7(jw)² + 7 jw + 4 = 2 w ⁴ – j4 w ³ – 7 w ² + 7j w + 4,

где , , , 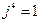и т. д.

Выделим вещественную и мнимую части.

U (w) = 2 w ⁴ – 7 w ² + 4;

V (w) = –4 w ³ + 7 w.

Давая различные значения частоте w, находим координаты U (w) и V (w)точек годографа Михайлова. Лучше начинать нахождение координат точек годографа с характерных точек, а именно: с точки при w ®0, при w ®¥, точек, в которых годограф пересекает оси координат, а затем найти координаты промежуточных точек годографа, при необходимости можно найти экстремумы годографа. Полученные значения заносим в таблицу. Строим годограф.

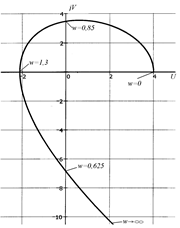
Рис. 1.65. Годограф Михайлова

Вывод:годограф Михайлова начинается на вещественно положительной полуоси и при изменении w от 0 до ¥ проходит против часовой стрелки 4 квадранта и в последнем уходит в бесконечность, где 4 – порядок характеристического уравнения системы. Таким образом система является устойчивой.

6. Анализ устойчивости по критерию Найквиста.

Критерий устойчивости Найквиста основан на использовании АФЧХ разомкнутой системы.

Для расчета частотных характеристик линейных звеньев и систем пользуются частотной передаточной функцией.

Частотной передаточной функцией называется отношение изображения Фурье выходной величины Y к изображению Фурье входного воздействия Х при нулевых начальных условиях.

Формально частотную передаточную функцию можно найти заменой в передаточной функции переменной p на переменную jw.

Частотная передаточная функция является комплексной функцией:

,

где Y (jw) и X (jw) – изображения Фурье выходной величины и входного воздействия;

U (w) – вещественная часть частотной передаточной функции;

V (ω) – мнимая часть частотной передаточной функции;

А (w) – модуль частотной передаточной функции;

φ(w) – аргумент частотной передаточной функции.

;

.

Модуль A (w) является АЧХ звена или системы, а аргумент φ(w) – ФЧХ звена или системы.

АЧХ и ФЧХ характеризуют реакцию системы или звена на гармоническое воздействие.

АЧХ называется зависимость отношения амплитуд выходного и входного гармонических сигналов от частоты в установившемся режиме.

ФЧХ называется зависимость разности фаз между выходным и входным сигналами от частоты в установившемся режиме.

АФЧХ характеризует зависимость отношения амплитуд и разности фаз от частоты одновременно.

Строится график АФЧХ в координатах U (w) и jV (w). Для этого рассчитываются U (w) и V (w) или А (w) и φ(w) при изменении частоты w от 0 до ∞. Длина вектора, соединяющего начало координат с графиком АФЧХ, равна значению А(w) при частоте w, а угол поворота от оси U равен φ(w) при частоте w.

7. Формулировка критерия Найквиста.

– Если система в разомкнутом состоянии устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от нуля до бесконечности не охватывала точку с координатами (–1; j 0).

– Если система в разомкнутом состоянии, находится на границе устойчивости (является астатической), то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы, дополненная дугой бесконечно большого радиуса против часовой стрелки до действительной полуоси, не охватывала точку с координатами (–1; j 0).

– Если система в разомкнутом состоянии неустойчива, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы охватывала точку c координатами (–1; j 0) в положительном направлении k /2 раз, где k – число корней характеристического уравнения с положительной действительной частью.

Разомкнутая система устойчива, если устойчивы все отдельные звенья системы после приведения ее к одноконтурной.

Определим устойчивость CAP для нашего случая.

Передаточная функция разомкнутой системы по задающему воздействию имеет вид:

.

Находим частотную передаточную функцию, подставляя jw вместо p:

.

Так как , , , и т. д., получим:

Для построения АФЧХ разомкнутой системы представим частотную передаточную функцию в виде:

W (jw) = U (w) + jV (w).

Чтобы представить частотную передаточную функцию в виде комплексного числа имеющего действительную U (w)и мнимую jV (w) части, умножим и разделим полученный результат на сопряженное знаменателю комплексное число и получим:

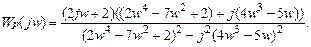
После преобразования

Вещественная часть частотной передаточной функции:

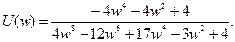
Мнимая часть частотной передаточной функции:

Давая различные значения частоте w, находим координаты U (w) и V (w)точек годографа. Лучше начинать нахождение координат точек годографа с характерных точек, а именно: с точки при w ®0, при w ®¥, точек, в которых годограф пересекает оси координат, а затем найти координаты промежуточных точек годографа, при необходимости можно найти экстремумы годографа.

Найдем координаты точек, которые являются местом пересечения годографа с осью абсцисс. Для этих точек координата по оси ординат равна нулю (V (w) = 0). То есть годограф пересекает ось U (w), если числитель V (w) равен нулю, а именно:

Решая это уравнение, находим корни. Для решения используем только положительные значения. В нашем случае w = 1,42.

Подставляя найденное значение w в выражение для U (w), находим координату искомой точки на оси абсцисс

По такому же методу найдем координаты точек пересечения годографа с осью ординат.

Полученные значения заносим в таблицу. Строим годограф (рис. 1.66).

Рис. 1.66. Годограф Найквиста

Вывод: АФЧХ разомкнутой системы не охватывает точку с координатами (–1; j 0), поэтому замкнутая система устойчива.

8. Определение запасов устойчивости.

При оценке устойчивости систем одного факта устойчивости недостаточно. Необходимо также оценивать величину запаса устойчивости, т. е. степени удаленности системы от границы устойчивости. Система, которая теоретически является устойчивой, но находится очень близко к границе устойчивости, при ее реализации может оказаться неустойчивой вследствие неточности математического описания системы, использованного при оценке устойчивости, вследствие приближенной практической реализации системы и неточностей при наладке, из-за изменения во времени параметров системы в процессе ее эксплуатации.

Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины – запас устойчивости по фазе Dj и запас устойчивости по амплитуде D A.

Запас устойчивости по фазе определяется величиной Dj, на которую должно возрасти запаздывание по фазе, чтобы система оказалась на границе устойчивости.

Запас устойчивости по амплитуде определяется величиной D A допустимого увеличения АЧХ, при котором система окажется на границе устойчивости. Таким образом, запас по амплитуде представляет собой запас по коэффициенту передачи разомкнутой системы по отношению к его критическому по устойчивости значению.

Величины Dj и D A показаны на рис. 1.66. Для определения Dj проводится дуга радиусом 1 до пересечения с АФЧХ. При проектировании САУ рекомендуется выбирать Dj ³ 30º и D A ³ 0,7. Для рассматриваемого примера CAP Dj» 35º, D A» 0,5, что удовлетворяет рекомендуемой величине запаса устойчивости по фазе, но не имеет достаточного амплитуде запаса по амплитуде.

Дата добавления: 2015-07-25