Размерность пространства и фракталы.

доклад прочитан 3 февраля 2007г. на семинаре “Мерность и фракталы”

Несколько слов о том, как возникла идея проведения семинара на эту тему. В некоторых литературных источниках Ордена встречаются упоминания о дробной мерности пространства. Несмотря на наличие высшего и даже специального образования, у читателя это вызвало лёгкое удивление и даже недоумение. Для устранения возникшего душевного дискомфорта дотошный читатель погрузился в специальную литературу и в Интернет, и его ум был просветлён! Действительно, с точки зрения современной науки, некоторые пространства могут иметь нецелую размерность. Эти пространства получили название фракталов. И, теперь, мы можем перейти к подробному рассмотрению возникших вопросов.

Все свойства Нашего Мира определяются пространством Вселенной. В определённом смысле, все материальные проявления Вселенной и есть само пространство, конфигурированное определённым образом. Поэтому, вопрос о размерности пространств представляется достаточно важным, для понимания их свойств. В физике применяется термин “физический вакуум”, подчёркивая его отличие от математических, континуальных (т.е. непрерывных) пространств. Однако, математика позволяет создавать информационные модели различных пространств, некоторые из которых существуют в материальном воплощении нашего мира. Именно поэтому, к сожалению для многих, в этом вопросе нельзя избежать применения математики. Но мы предприняли серьёзные шаги, чтобы смягчить травмирующее воздействие изложения и снабдили доклад множеством поясняющих, цветных картинок, которые, надеюсь, помогут разобраться в сути дела.

Размерность.

Понятие размерности является фундаментальным понятием в физике и математике. Сначала под размерностью понимали минимальное число параметров, необходимых для описания положения точки в пространстве. Действительно, на плоскости требуется задать две координаты точки, на отрезке достаточно одной. Несостоятельность такого наивного восприятия размерности стала очевидной после открытия взаимно однозначного соответствия между точками отрезка и квадрата и непрерывного отображения отрезка на квадрат. Первое из них было построено Кантором, второе — Пеано. Действительно, рассмотрим точку, принадлежащую единичному квадрату (Рис.1.) с координатами x=0,a₁a₂a₃… и y=0,b₁b₂b₃… в виде десятичных дробей. Здесь a_i и b_i — цифры в десятичной записи дробей. Сопоставим этой точке точку единичного отрезка с координатой z=0,a₁b₁a₂b₂a₃b₃…

Рис.1. Отображение квадрата на отрезок.

Ясно, что разным точкам единичного квадрата таким отображением сопоставляются разные точки отрезка. При небольших и вполне очевидных уточнениях получаем взаимно однозначное отображение квадрата в отрезок. Это отображение и предложил Георг Кантор (3 марта 1845, Санкт-Петербург — 6 января 1918, Халле (Заале) — немецкий математик), показав тем самым, что определение размерности, упомянутое выше, неудовлетворительно, так как не сохраняется при взаимно однозначных отображениях. Совершенно аналогичным образом можно установить однозначное соответствие между точками единичного отрезка и единичного куба, в том числе n–мерного. Наличие этих отображений привело к исчезновению ощущений, что квадрат или куб богаче отрезка по числу точек, и оказалось, что размерность может меняться при взаимно однозначных отображениях и возрастать при однозначных непрерывных отображениях. Указанное обстоятельство оказалось полной неожиданностью для большинства математиков — современников Георга Кантора и вызвало массовое неприятие его идей. Впоследствии, это привело к длительной депрессии учёного и значительному ухудшению его душевного здоровья. Однако, в отображениях Кантора заключён глубокий смысл. Они показывают, что континуальные пространства любой размерности имеют общий «фундамент». Математика определяет мощность множеств, образующих пространства любой размерности, как эквивалентные. Но любой человек интуитивно понимает различие между одномерным, двумерным или трёхмерным пространствами. Так в чём заключается это различие? Различие заключено в способе организации элементов различных пространств — точек. Последовательное увеличение размерности пространства приводит к естественному структурированию пространства, уменьшению его энтропии, появлению возможности образования новых объектов и их движения. Например, в 0-мерном пространстве — точке отсутствует внутренняя структура и возможность любого движения. В одномерном пространстве уже возможно образование линейных структур и перемещение их в двух направлениях. Понятно, что в 3х-мерном пространстве возможности структурирования объектов и их движенья неизмеримо выше. Таким образом, можно сделать вывод о значительной «информационной насыщенности» пространств высшей размерности. Многие свойства математических пространств нашли своё отражение в реальном физическом пространстве и фактически являются частью его “информационного фундамента”. Указанное обстоятельство косвенным образом подтверждает представления, развиваемые в Ордене, о существовании информационной основы материального мира, определяющей его основные проявления. Из всего сказанного становится понятно, что размерность является важнейшей характеристикой пространства, поэтому, возникла необходимость в уточнении и строгом определении понятия размерности.

Топологическая размерность.

Именно Пуанкаре (Жюль Анри Пуанкаре (фр. Jules Henri Poincare; 1854—1912) — французский математик, физик и теоретик науки; один из величайших математиков Франции, член Парижской АН (с 1887) и с 1908 Французской академии.) обратил внимание на необходимость анализа понятия размерности и указал на "индуктивную" природу этого понятия. Согласно его идее «пространству» (или множеству) следует приписывать размерность n, если две его точки могут быть отделены удалением подмножества точек размерности n–1 (Рис.2.). Далее для обозначения размерности пространства (или множества) X будем использовать принятое обозначение Dim{X}=n.

Рис.2. Отделение точек множеством меньшей размерности.

Исходя из этой идеи, определим индуктивную размерность следующим образом:

1. Dim{∅}= -1, ∅ — пустое множество.

2. Размерность пространства X есть наименьшее целое число n, такое, что каждая точка пространства обладает окрестностями, границы которых имеют размерность меньшую n.

Найдем согласно определению размерность точки. Ясно, что для отделения точки не требуется ничего. Следовательно, для ее отделения достаточно пустого множества {∅}. Тогда размерность точки на единицу больше размерности пустого множества Dim{point}=1+ Dim{∅}=1 - 1=0. Таким образом, размерность точки равна 0. Аналогично можно установить теперь размерность отрезка и более сложных множеств. Очевидно, что определенная таким образом размерность может принимать только целые значения. При развитии теории размерности был обнаружен и другой путь ее определения. Для простоты изложим эту идею в двумерном случае. Рассмотрим двумерную область и разделим ее на маленькие ячейки, которые содержат свою границу (Рис. 3).

Рис.3. Покрытие квадрата ячейками.

Отмечена точка, принадлежащая сразу трем ячейкам. Меняя разбиение на ячейки нельзя добиться исчезновения таких точек, принадлежащих не менее чем трем ячейкам.

Легко заметить, что каковым бы ни было такое разбиение и форма ячеек, всегда найдутся точки, принадлежащие одновременно 3-м ячейкам. Это наблюдение привело к теореме Лебега-Брауэра: если n-мерная фигура разбита на достаточно малые ячейки, то непременно существуют точки этой фигуры, принадлежащие по меньшей мере n+1 ячейкам. Таким образом, приходим к определению размерности, которая сохраняется при непрерывных взаимооднозначных отображениях и является топологическим инвариантом. Это означает, что никакие множества не могут быть топологически эквивалентными, обладая разной размерностью. По этой причине определенную выше размерность также будем называть топологической размерностью пространства X. Теперь мы знаем, что топологическую размерность пространства можно определить двумя путям, отделяя две точки или покрывая его достаточно малыми ячейками. И здесь необходимо подчеркнуть два важных момента:

1. Топологическая размерность всегда целое число.

2. Для пустого множества её значение равно –1.

Размерность Хаусдорфа.

Рис.4. Покрытие объекта n-мерными кубиками.

Важность теоремы Лебега-Брауэра, кроме практических следствий, связана с интуитивным чувством, что существует связь между покрытием и размерностью, а, следовательно, размерностью и мерой. Замечательный подход к определению размерности, основанный на этом, предложил Феликс Хаусдорф, немецкий математик (нем. Felix Hausdorff; 8 ноября 1868, Бреслау — 26 января 1942, Бонн) — считается одним из основоположников современной топологии. Теперь введенная им размерность называется размерностью Хаусдорфа. Повторим его путь, разумеется, в несколько упрощённом виде. Пусть в n–мерном пространстве размещен некоторый геометрический объект (Рис.4.). Покроем его n–мерными кубиками размера e. Каждая точка нашего объекта будет принадлежать одному из кубиков. Кубики, в которых нет точек нашего объекта, естественно, учитывать не будем.

Рис.5. Зависимость предела m_p при e→0

Построим теперь сумму по всем кубикам, покрывающим объект, вида m_p=∑e^p, (Рис.5), где p — произвольный действительный параметр. Теперь устремим размер кубиков e к нулю и посмотрим, как зависит значение этого предела от параметра p. Оказывается, что этот предел (Рис.5.) при малых e равен ∞, а при больших 0. Важно, что существует значение n, при котором происходит скачок от 0 к ∞. Это значение D_H и называется размерностью Хаусдорфа.

Существуют фрактальные множества, имеющие одинаковую размерность Хаусдорфа, но отличающиеся по значениям предела при p=D_H.

Проведенные рассуждения позволяют получить общее выражение для вычисления D_H:

DH =

lim e→0

[lnN(e)/ln(1/e)]

Посмотрим, чему равна размерность Хаусдорфа знакомых геометрических объектов, например, единичного квадрата Q (Рис.5а.).

Рис.5а.

Его топологическая размерность с очевидностью равна 2. Для этого покроем его квадратиками размером e. Приведенная выше сумма или мера Хаусдорфа равна e^p, умноженная на число членов суммы, так как все вклады в нее одинаковы. Число квадратиков размером e, покрывающих квадрат Q, легко подсчитать, и оно равно N(e)=e^-2. Тогда

m_p(Q)=N(e)e^p=e^p-2.

Легко видеть, что если p›2, то эта сумма пропорциональна положительной степени e и при стремлении e к нулю обращается в нуль. При p‹2 сумма пропорциональна отрицательной степени e, и предел при e→0 равен ∞. Тогда согласно определению, приведенному выше, размерность Хаусдорфа квадрата Q

D_H(Q)=2.

Таким образом, для обычных и знакомых множеств размерность Хаусдорфа совпадает с их топологической размерностью

D_H(Q)=DimQ.

Это утверждение мы проверили для квадрата, аналогично легко проверить его для отрезка или куба.

Однако всегда ли это так? Рассмотрим для этого один из самых популярных примеров фрактального множества — Канторово множество. Этот пример множества впервые был предложен Кантором. Цель, которую он преследовал, — это указать пример множества, состоящего из отдельных точек, но имеющих их столько, сколько и любой отрезок действительной оси. Точнее, мощность этих множеств одинакова. В этом смысле отрезок, который мы легко признаем за линию, по мощности не отличим от Канторова множества K. Построение такого множества является очень простым и демонстрирует часто применяемую и сейчас идею построения идеальных фрактальных множеств. В основе лежит идея итераций, или последовательного применения некоторой операции. Возьмем без потери общности единичный отрезок (Рис.6).

Рис.6. Процедура построения Канторового множества. Показаны четыре первых этапа.

Наша операция заключается в делении отрезка на 3 равные части и отбрасывании центральной части. После первого шага получим 2 отрезка длиной 1/3. Повторим операцию с каждым полученным отрезком на предыдущем шаге. Тогда на втором этапе получим 4 отрезка длиной 1/9 (см. Рис. 6). На n–шаге получим 2ⁿ отрезков длиной 1/3ⁿ. Теперь предположим, что мы повторим эту процедуру построения бесконечное число раз. Полученное множество и будет Канторовым множеством K. Между любыми двумя точками Канторова множества есть точки, не принадлежащие ему. Это означает, что топологическая размерность этого множества Dim{K}=0. Определим теперь его размерность Хаусдорфа. Для этого покроем его на n–шаге построения отрезками длиной 1/3ⁿ и вычислим меру Хаусдорфа. Опуская достаточно простые промежуточные вычисления приходим к следующему численному результату

D_H{K}=ln2/ln3 ≈ 0,6309.

Число отрезков, покрывающих его на n–шаге, также легко вычислить N(e_n)=2ⁿ. Тогда выразим N(en) через en. Это легко сделать, используя элементарные преобразования

N(e_n)=2ⁿ≡eⁿln2 ≡ e^{n*ln2*ln3/ln3}≡(e^ln3)^n*ln2/ln3≡(3^-n)^-ln2/ln3≡(e_n)^-ln2/ln3

.

Аналогично получаем N(e_n)=e_n^-ln2/ln3. (1)

Теперь подставим полученное выражение в меру Хаусдорфа

m_p(K)=N(e)e^p-ln2/ln3

.

При n→∞ длина элементарных отрезков e_n→0 и легко видеть, что размерность Хаусдорфа

D_H{K}=ln2/ln3

.

Установленный факт позволяет сделать несколько важных выводов. Прежде всего, существуют множества, размерность Хаусдорфа которых не равна целому числу. Топологическая размерность их всегда целое число. Реальным примером таких множеств является Канторово множество. Заметим, что для него топологическая размерность Dim{K}=0 и, следовательно, Dim{K}‹D_H{K}.

Теперь, в качестве рабочего определения фрактальных множеств будем использовать это свойство. Другими словами, самоподобные множества, у которых размерность Хаусдорфа больше топологической размерности, будем называть фрактальными множествами. Свойство самоподобия Канторова множества очевидно по построению. Действительно, если мы возьмем часть множества, принадлежащую отрезку [0, 1/3], и растянем его в 3 раза, то точки этого множества при наложении на все Канторово множество в точности совпадут с точками всего Канторова множества K. В этом примере самоподобие является точным, а не статистическим. Однако в определении фрактальных множеств допускается и статистическое подобие. Причина этого очевидна. В природе значительно чаще встречается статистическое подобие. Обратим внимание, что свойство самоподобия никак не связано с дробностью размерности Хаусдорфа, и на первый взгляд его включение в определение фрактальных множеств или объектов кажется искусственным. Зачем использовать его, обсудим позже.

Вернемся к размерности Хаусдорфа. Теперь ясно, что с ее помощью можно количественно охарактеризовать различия в геометрическом устройстве множеств, имеющих одинаковые топологические размерности. Так, одна точка имеет такую же топологическую размерность Dim{point}=0, как и Канторово множество Dim{K}=0. Однако геометрическая структура этих множеств с очевидностью различна. В определенном смысле этот тонкий инструмент позволяет сделать заключение, к какому обычному геометрическому объекту — точке, отрезку или квадрату – ближе конкретное экзотическое фрактальное множество. Однако определение размерности Хаусдорфа содержит несколько предельных операций, которые затрудняют ее использование для реальных физических объектов. Конечно, довольно легко мы нашли ее для идеализированного фрактального множества – Канторова множества. Однако, если мы попытаемся ее определить для реального горного массива, нас ожидают существенные трудности. Одна из них – это существование атомов.

Фракталы и фрактальные пространства.

Теперь, когда мы получили некоторое представление о размерности пространства, попытаемся разобраться в таком понятии, как фрактал. Фрактал (лат. fractus — “дроблёный”) — термин, введённый (фр. математиком) Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных математических структур, т. е., состоящих из частей, которые в каком-то смысле подобны целому. Рождение фрактальной геометрии принято связывать с выходом в 1977 году его книги “Фрактальная геометрия природы”. История фракталов началась с геометрических фракталов, которые исследовались математиками в 19 веке. Фракталы этого класса самые наглядные, потому что в них сразу видна самоподобность при любых масштабах наблюдения. В двухмерном случае такие фракталы можно получить задав некоторую ломаную, называемую генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры (а, точнее, при переходе к пределу) получается фрактальная кривая. При видимой сложности полученной кривой, её общий вид задается только формой генератора. Примерами таких кривых служат: кривая Коха (Рис.7), кривая Пeано (Рис.8), кривая Минковского.

Рис.7. Кривая Коха.

Рис.8. Кривая Пеано.

К геометрическим фракталам также относят фракталы получаемые похожими процедурами, например: множество Кантора, треугольник Серпинского, снежинка Коха и др.

Рис.9. Треугольник Серпинского.

Рис.10. Снежинка Коха.

Снежинка Коха, например, интересна тем, что имеет конечную площадь и бесконечный периметр (Рис.10.). Интересен, также следующий факт: у геометрических фракталов не существует касательных, в отличие от обычных геометрических поверхностей и фигур. Это означает, что аналитические функции, описывающие их, нигде не дифференцируемы. Т.е. у фракталов нет производных.

Теперь, уяснив особенности геометрических фракталов, мы можем сформулировать подмеченные наблюдения. В то время как гладкая евклидова линия заполняет в точности одномерное пространство, фрактальная линия выходит за пределы одномерного пространства, вторгаясь в двумерное. Таким образом, фрактальная размерность кривых Коха или Минковского будет находиться между 1 и 2. Рассмотрим, теперь, классификации фракталов.

Классификации фракталов.

В основном, фракталы делят на геометрические, алгебраические и стохастические. Однако, существуют и другие классификации, например: Рукотворные и природные. К рукотворным относятся те фракталы, которые были придуманы учёными, они при любом масштабе обладают фрактальными свойствами. На природные фракталы накладывается ограничение на область их существования — т. е. максимальный и минимальный размер, при которых у объекта наблюдаются фрактальные свойства. Детерминированные (алгебраические и геометрические) и недетерминированные (стохастические).

Примеры геометрических фракталов приведены выше, рассмотрим теперь алгебраические фракталы. Алгебраические фракталы получили свое название за то, что их строят, используя простые алгебраические формулы. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. Состояние, в котором окажется динамическая система после некоторого числа итераций, зависит от начальных условий. Поэтому каждое устойчивое состояние (аттрактор) обладает некоторой областью начальных состояний, при которых система обязательно перейдет в рассматриваемые конечные состояния. Таким образом, фазовое пространство разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры (Рис.11, 12.).

Рис.11.
Множество Мандельброта.

Рис.12. Множество Жюлиа.

Алгоритм построения достаточно прост и основан на простом итеративном выражении: z_i+1 = F(z_i), где F(z_i) - какая-либо функция комплексной переменной. Т. е. каждое последующее значение z вычисляется как функция предидущего. Для всех точек прямоугольной или квадратной области на комплексной плоскости вычисляем достаточно большое количество раз z_i+1 = F(z_i), каждый раз находя абсолютное значение z. При этом значения функции для разных точек комплексной плоскости могут иметь разное поведение:

· |z| стремится к бесконечности;

· |z| стремится к 0;

· |z| принимает несколько фиксированных значений и не выходит за их пределы;

· поведение |z| хаотично, без каких-либо тенденций.

Одним из самых распространённых способов раскрашивания точек будет сравнение |z| с заранее выбранным числом, которое считается “бесконечным”, т. е. цвет точки равен номеру итерации, на которой |z| достиг “бесконечности” или чёрному в противном случае. Интересный факт, некоторые алгебраические фракталы поразительным образом напоминают изображения животных, растений и других биологических объектов, вследствие чего получили название биоморфов (Рис.13.).

Рис.13. Биоморфы.

Стохастические фракталы. Фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры, называются стохастическими. Термин “стохастичность” происходит от греческого слова, обозначающего “предположение”. К слову сказать, большинство природных фракталов – стохастичны.

Размерность природных фракталов.

В первой части семинара мы получили представление о размерности пространств и множеств, а также, способах её определения. Теперь мы знаем, что размерность можно определить, заполняя (покрывая) пространство геометрической фигуры, некоторой мерой (единицей измерения). Если выбраная мера не соответсвует её размерности, мы получим ноль или бесконечность. И, только, в случае их совпадения получим конечный результат. Например, если мы будем измерять длину прямой, то метровых отрезков в ней будет N, полуметровых 2N, дециметровых — 10N и так далее. В данном случае наблюдается прямая пропорциональная зависимость. В случае измерения площади мы уже получим следующие значения: 4N, 100N, т. е. здесь зависимость уже квадратичная. Объём трёхмерных фигур пропорционален кубу их линейных размеров. Однако, настойчивое стремление измерить площадь единичного квадрата при помощи единичного отрезка приведёт к глубокому разочарованию и бесконечному результату. Попытка измерить площадь с помощью единичного кубика способна ввергнуть любознательного экспериментатора в ещё более глубокую депрессию, ибо результат будет нулевым. И только опытный агроном сразу скажет, что квадратную площадь можно измерить только квадратными единицами! Если попытаться применить эти правила к реальным фрактальным объектам, возникает парадоксальная ситуация — их размерность окажется дробным числом. Так как фрактал состоит из бесконечного числа повторяющихся элементов, невозможно точно измерить его длину. Это означает, что чем более точным инструментом мы будем его измерять, тем большей окажется его длина. Хорошим примером сказанному является история измерения береговой линии островов и материков (Рис.14).

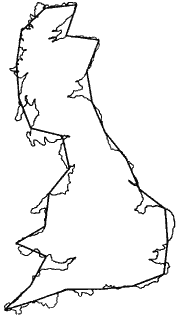
Рис.14.
Береговая линия побережья Великобритании.

Опыт показывает, что длина береговой линии L зависит от масштаба l, которым проводятся измерения, и увеличивается с уменьшением последнего по степенному закону L = Λ * l^–α, где Λ = const. Так, например, для побережья Великобритании α≈0.3. Происхождение такой зависимости понятно: чем меньше масштаб мы используем, тем меньшие детали побережья будут учтены и дадут вклад в измеряемую длину. Наоборот, увеличивая масштаб, мы “спрямляем” побережье, уменьшаем тем самым его длину L. Число раз N, которое измерительный масштаб l укладывается вдоль побережья, равно: N=L/l = Λ * l^–(1+α).

По нашей терминологии береговая линия Великобритании представляет собой фрактал с размерностью D=1+α≈1.3.

Было обнаружено, что фрактальная размерность побережья существенно зависит от его геологической структуры и может изменяться между 1,01 и 1,6, для различных районов.

Самым удивительным оказывается то, что и многие живые природные объекты обладают дробной размерностью. Например, размерность кровеносной системы человека лежит между 2,4 и 2,6 (Рис.15.). При различных масштабах наблюдения характер распределения кровеносных сосудов существенно не изменяется.

Рис.15.
Кровеносная система человека.

Вообще говоря, фрактальный принцип питания многоклеточных организмов оказался гениальным изобретением, практически снявшим ограничения на размеры организмов, связанные с диффузионным характером питания. Внутренние слои клеток древнейших многоклеточных получали питание и кислород путём диффузии через периферийные слои клеток. Этот медленный процесс остановил рост первых организмов на микроскопическом уровне. Уже у насекомых появились раздельные системы питания и дыхания, использующие фрактальный принцип организации. В дальнейшем оказалось, что оптимальным является “применение” совмещённой системы питания и дыхания на основе гемоглобина и использование, так сказать, “турбонаддува” в виде лёгких. Этот принцип позволил достичь самых больших размеров организмов на Земле у динозавров и млекопитающих.

Рис.16.
Фрактальная структура дерева.

Следует отметить, что, применяя этот “принцип”, организмы могли быть и значительно больше, но их рост был ограничен гравитацией Земли. Известно, что сила мышц увеличивается пропорционально их сечению (т.е. 2-ой степени линейного размера), а вес растёт пропорционально объёму тела (т.е. 3-ей степени линейного размера), — значительно быстрее. Это означает, что при гигантских размерах животное теряет способность двигаться, а, значит, питаться. Для неподвижных живых организмов это ограничение наступает значительно позже, поэтому самыми большими организмами на Земле являются деревья (вес сотни тонн) (Рис.16.).

Кстати говоря, фрактальный принцип организации питания и дыхания у деревьев прослеживается в структуре корневой системы и кроны. Здесь уместно вспомнить “фрактальное” свойство дерева, подмеченное ещё Леонардо Да-Винчи, — общее сечение всех ветвей в самой широкой части кроны равно толщине ствола. Если бы отсутствовали гравитация и ветер, то фрактал кроны рос бы неограниченно.

Теперь мы можем сформулировать следующее наблюдение. Чем больше размерность фрактала, тем больше вероятность, что заданная область пространства содержит фрагмент этого фрактала.

Фрактальная размерность.

Математические исследования по теории размерности долгое время оставались вне интересов физики. Интерес к фрактальным (или совершенным) множествам в физике возник и возрастал в значительной мере благодаря работам Мандельброта. Замечательные и оригинальные по стилю книги [3, 4], написанные им, содержат не только необходимые понятия фрактальной физики и широкий круг новых идей, но и пронизаны духом творчества, увлекающим читателя. Основная его идея была связана с выделением объектов (множеств), обладающих самоподобием, т. е. таких, что часть множества в определенном смысле подобна всему множеству. Другими словами, такие множества являются масштабно инвариантными. Это означает, что выделяя часть множества и изменяя масштаб подходящим образом, мы получаем новое множество либо совпадающее точно с исходным полным множеством, либо совпадающее статистически по заданной вероятной мере. Такое самоподобие может возникать как в результате итерационной процедуры построения, так и по более глубоким физическим причинам. В частности, самоподобие ранее обсуждавшегося Канторова множества или кривой Пеано очевидно и является результатом используемой простой итерационной схемы их построения. Важность этой идеи — в выделении некоторых элементарных кирпичиков или объектов, сохраняющих универсальные свойства с изменением (обычно уменьшением) масштабов измерения e. Это означает, что эти свойства могут быть обнаружены не только в пределе e→0, как при определении размерности Хаусдорфа, но в целой конечной области изменения масштабов e. В свою очередь, это приводит как к возникновению новых характеристик таких множеств (например: фрактальная размерность), так и к возникновению более простых и эффективных методов их исследования.

Действительно, анализируя выражение для самоподобного Канторового множества (1), можно понять, что если часть подобна целому, то это выражение выполняется не только в пределе, но и на конечных, достаточно малых масштабах покрытия. Тогда его можно упростить и записать в виде

N(e)≈e^-D_F, (2)

где N(e) — число окрестностей с характерным размером e, содержащее точки рассматриваемого множества, а D_F — по определению, фрактальная размерность множества или клеточная размерность.

Здесь уместно сделать небольшое замечание о смысле масштаба разрешения e. Ясно, что абсолютная величина окрестности не важна. Только по этому значению нельзя даже сказать, мала или велика эта окрестность. Об этом можно судить, сравнивая ее с величиной объекта. Поэтому в качестве масштаба разрешения e нужно использовать относительный масштаб e = l/L, где l — размер окрестности, а L — размер объекта. Во всех предыдущих случаях под e также следует понимать именно такой масштаб разрешения. Это важно даже для Канторова множества, где e = l/1, так как длина исходного отрезка была выбрана единичной L = 1. При таком понимании e (относительного масштаба) формулы не зависят от выбора единиц измерений.

Из определения ясно, что D_F является количественной характеристикой самоподобия, т. е. указывает, каким образом нужно изменить масштаб, чтобы выбранная часть совпадала со всем множеством. Естественно возникает вопрос, как фрактальная размерность связана с размерностью Хаусдорфа. Это довольно сложный вопрос. Оказывается, эти две размерности не всегда совпадают. Обсуждение этого вопроса требует уже более серьезной математики и выйдет за рамки популярного доклада. Дополнительно важно подчеркнуть, что фрактальные множества могут обладать одинаковыми фрактальными размерностями, но отличаться другими своими характеристиками. Часть этих характеристик уже известна и введена, но многое еще предстоит открыть на этом пути. Используя в качестве определения фрактальную размерность, оказалось достаточно просто определять ее из физических экспериментов, и к настоящему времени обнаружено гигантское число физических объектов и процессов, обладающих нецелой фрактальной размерностью. Поэтому фрактальные объекты и процессы стали неотъемлемой частью физики. Другая возможность обобщения видна из физических представлений о возникновении фрактальных кластеров и их росте. Действительно, в этом случае существует минимальный масштаб — размер частиц. Поэтому размер покрытия стремить к нулю бессодержательно. Однако размер кластера в процессе роста неограничен сверху. Это означает, что можно увеличивать размер ячейки или покрытия до ∞. Это позволяет ввести глобальную размерность кластера при e→∞. Обычное определение тогда характеризуется как определение локальной клеточной размерности.

Следующий этап обобщения идеи скейлинга (cкейлинг — пропорциональное изменение размеров, масштабирование объекта) привел к так называемым самоафинным фракталам и соответственно к другим характеристикам этих объектов. Дело в том, что, говоря о масштабной инвариантности множеств, мы подразумеваем, что пространство, в которое погружено рассматриваемое множество, напоминает евклидово пространство, координаты которого равноправны. При этом масштабное преобразование действует на все координаты одинаковым образом. Как с физической, так и математической точки зрения это далеко не всегда так. Достаточно упомянуть пространство-время, в котором масштабные преобразования могут осуществляться по пространственным и временным координатам как независимые. Для объектов типа траекторий в этом пространстве коэффициент подобия по времени и координате вовсе не обязан быть одинаковым.

Разумеется, существует большое число проблем, которые здесь не обсуждаются. Это и математические строгие результаты, полученные в последнее время по обоснованию фракталов. Интересны результаты по анизотропным фракталам. Проблему последних легко представить, если задуматься над определением размерности таких объектов, как деревья или реки со всеми притоками, впадающими в основное русло.

Ясно также, что из элементарных кирпичиков можно построить уже более сложные объекты, приготовив смесь из фрактальных множеств с разными фрактальными размерностями. При этом их смесь можно сделать не только в геометрически разных частях, но и, что более интересно, на разных масштабах измерения, но это уже другая история.

Информационно–пространственные фракталы.

Черезвычайно интересным представляется применение фрактальных принципов в области хранения и преобразования информации. Известно, что информация не является материей, скорее это способ организации (упорядочения) материальных объектов. Информация не существует вне пространства и для неё всегда требуется материальный носитель с соответствующим способом хранения и преобразования информации. Причём, содержание информации никак не связано с видом носителя. Однако принципы хранения и преобразования информации могут быть различными. Например, наиболее часто применяемый в компъютерной технике способ определения объектов состоит в последовательном описании отдельных элементов и их взаимосвязей. У этого способа есть очевидное достоинство и два столь же очевидных недостатка. Способ требует минимального количества единиц информации для описания объекта, но последовательное (поэлементное) преобразование информации является очень медленным. Кроме того, единичная ошибка даже в одном элементе описания иногда способна полностью исказить образ объекта. Известен другой принцип. Если осветить выбраный объект, например кубик, потоком световых квантов (носителей информации), то каждая точка поверхности кубика становится элементарным излучателем рассеянного света, несущего в окружающее пространство информацию о свойствах этой точки. Таким образом, в окружающем объект пространстве содержится информация о всей его поверхности. Отражённый свет формирует уникальный волновой фронт, который распознаётся нами в виде образа объекта – кубика. Если в качестве источника света использовать лазер, то возникает техническая возможность зафиксировать пространственную структуру волнового фронта с помощью фотоэмульсии. Последующее освещение полученного отпечатка полностью восстанавливает волновой фронт и зрительный образ объекта. Это хорошо известный теперь принцип голографии. Уже в первых экспериментах по неосторожному обащению со стеклянными фотопластинками было обнаружено удивительное свойство голограмм — даже небольшие их фрагменты были способны воспроизводить изображение объекта целиком, правда с худшим разрешением. Это понятно, т.к. каждый элемент голограммы формируется отражённым светом всех точек поверхности объекта. Из этого следует, что информация об объекте распределена по всей голограме однородным образом, причём информационное содержание любого фрагмента голограммы подобно всей информации в целом. Это яркий пример информационного подобия части и целого в широком диапазоне пространственных масштабов хорошо соответствует определению фрактала. Причём, это не геометрический фрактал, здесь нет точного подобия структурных пространственных единиц голограммы на различных масштабах. Здесь мы имеем пример информационного подобия фрагментов голограммы различных размеров. Именно поэтому, термин — информационно-пространственный — точно соответствует этому типу фракталов, т.к. информационное подобие неразрывно связано с пространством существования информации. У описанного способа преобразования информации есть один очевидный недостаток и два столь же очевидных достоинства. Недостаток состоит в информационной избыточности способа, особенно при фиксации абстрактных объектов. При отражении реальных, природных объектов, обладающих индивидуальностью, голографический способ затрачивает существенно меньшие объёмы информации, благодаря физическому принципу сжатия изображения. В то же время запись и воспроизведение информации происходят за один шаг. Кроме того, надёжность хранения информации здесь неизмеримо выше, ведь даже потеря значительной части голограммы не изменит смысловой сущности фиксируемого образа. Проведенные в последнее десятилетие исследования функций человеческого мозга позволили в значительной мере установить основные принципы формирования памяти и психической деятельности. Ряд учёных даже был удостоен Нобелевской премии за цикл исследований на эту тему. По современным представлениям, механизм памяти несколько напоминает голографический принцип. Экспериментальными исследованиями было установлено, что память имеет распределённую структуру, это означает, что различные образы памяти не имеют конкретной локализации в физическом пространстве мозга. Известны клинические случаи потери значительной части мозгового вешества (более 25%) практически не влияющие на информационное содержание памяти. В то же время, память о конкретном объекте хранится в виде образов этого объекта в различных обстоятельствах. Их очень много и они распределены по всему нейронному массиву мозга. Поэтому потеря части мозгового вещества приводит к потере только памяти об объекте при определённых обстоятельствах, а не к потере памяти об объекте вообще. В обычных обстоятельствах отдельные образы конкретного объекта образуют сложную иерархическую структуру, являющуюся базисом ассоциативного механизма работы памяти. На вершине иерархической структуры находится сложный символ-образ, отражающий основные свойства объекта. По мере возбуждения нейронной структуры мозга происходит погружение в более глубокие слои иерархической системы образов и их осознание. Принципиально человек помнит весь поток информации, полученный с помощью органов чувств, на протяжении всей жизни. Это доказывают отдельные личности, обладающие 100% памятью на все обстоятельства своей жизни. Наше “умение забывать” всего лишь защитный механизм, позволяющий ограничить бесконечный поток ассоциаций из глубин мозга и выделить жизненно важную, в данный момент, информацию. Таким образом, каждая иерархическая структура памяти, соответствующая конкретному объекту, обладает стохастическим подобием составляющих её элементов, с точностью до вариации конкретных обстоятельств, а, значит, является информационно-пространственным стохастическим фракталом. Указанное обстоятельство, позволяет по-новому взглянуть на изменение терминологии в отношении мозга, принятое в Ордене. Применяемый, в настоящее время, термин “фрактальный реактор” более точно соответствует сущности человеческого мозга.

Пространства высшей размерности.

До сих пор мы рассматривали пространства и множества с размерностью не превышающей 3-х и, поэтому, достаточно легко представимых человеческим воображением. Однако, математики с лёгкостью оперируют объектами в многомерных и, даже, бесконечномерных пространствах. Закономерно возникают вопросы: Как представить себе многомерные объекты?; Существуют ли реально некоторые из них в окружающем нас мире?; Возможны ли какие-либо эксперименты с многомерными объектами и пространствами?

Рис.17. Плоская Вселенная.

К сожалению, прямая попытка ответить на эти вопросы наталкивается на трудность восприятия образов многомерных объектов. Чтобы как-то решить эту проблему воспользуемся методом аналогий. Сначала попробуем определить, какие явления в окружающем нас мире могут быть вызваны проявлением пространства с размерностью больше 3-х. Многие из нас слышали о “раширяющейся Вселенной”. Суть явления состоит в том, что все точки физического пространства нашей Вселенной удаляются друг от друга со скоростью, возрастающей с расстоянием между ними. Этот экспериментальный факт, обнаруженный астрофизиками в прошлом веке, установлен достаточно надёжно. Наиболее простое объяснение этого явления состоит в том, что наше физическое 3-х-мерное пространство представляет собой поверхность 4-х-мерной гиперсферы, раширяющейся из центра с некоторой скоростью. Воспользуемся методом аналогий, чтобы представить себе это явление. На рис.17 изображена 3-х-мерная сфера, расширяющаяся в 3-х-мерном пространстве. 2-мерная поверхность сферы является аналогом нашего 3-х-мерного пространства. Из рис.17. легко понять каким образом возрастает расстояние между всеми точками поверхности сферы. Предположим, теперь, что в поверхности этой сферы возникла разумная жизнь и, даже, высокоразвитая цивилизация во главе с плоскими зелёными человечками. Естественно предположить, что в конце концов к ним в голову прийдут мысли подобные нашим и они попытаются использовать достижения своей цивилизации для измерения расстояний в недоступном для них 3-м измерении. В результате напряжённой работы им удалось создать прибор для измерения расстояний (на рис.17. он изображён в виде линейки) и, героичесчким усилием развернуть его в 3-е измерение. Каков же будет результат этого, без сомнения, грандиозного эксперимента? Выход в 3-е измерение приведёт к мгновенному исчезновению “линейки” из наблюдательного пространства. В лучшем случае, в распоряжении местных плоских учёных окажется область пересечения 2-мерной “линейки” и 2-мерного пространства. Этя область пересечения пространств одной размерности всегда имеет размерность меньше на 1. В случае 2-мерных объектов область пересечения будет одномерной, т.е. отрезком линии. Нам доподлинно не известны технологические возможности “плоской цивилизации” по обнаружению одномерных объектов, поэтому, проанализируем создавшуюся ситуацию с позиций нашего 3-х-мерного мира, возможности которого нам известны лучше. В нашем случае, “разворот линейки” в 4-е измерение приведёт также к результату, который врачи называют обычно — “мы его потеряли”. В нашем распоряжении останется уже 2-мерный объект, образованный пересечением 3-х-мерной линейки с нашим пространством. Это лучше, чем 1-мерный объект в предидущем случае, но, посмотрим, достаточно ли этого для его обнаружения. Нашему общению с окружающим миром мы обязаны очень небольшому количеству фундаментальных взаимодействий, обеспечивающих функционирование не только наших чувств, но и всех наших приборов. Носителями этих взаимодействий являются 3-х-мерные объекты — элементарные частицы. Наиболее распространённым видом взаимодействия, с помощью которого мы получаем более 99% информации об окружающем мире, является электромагнитное. Мы видим и ощущаем окружающие предметы потому, что свет взаимодействует с пространственным распределением электрических зарядов в них. Проще говоря, степень “видимости” объекта напрямую зависит от количества зарядов в единице объёма тела. В 2-мерном “следе”, оставшемся в нашем пространстве, объёмная плотность заряда всегда равна 0, т.к. 3-е измерение отсутствует. Поэтому, свет будет беспрепятственно проходить через 2-мерное сечение, без рассеяния и отражения и мы ничего не увидим. Попытка “пощупать” 2-мерное пространство также окончится неудачей, т.к. электронные оболочки атомов нашей кожы не встретят сопротивления электрических зарядов атомов “линейки”. Детальный анализ других известных типов взаимодействий, в рассмотренной ситуации, приводит к тому же результату. Этот вывод послужил основой для различных теорий “множественных вселенных”, т.к. даже пересекающиеся вселенные не взаимодействуют и не влияют друг на друга. Рассмотрим, теперь, как взаимодействует “полноценное” 4-х-мерное тело с нашим 3-х-мерным пространством. Для примера возьмём 4-х-мерный шар, как наиболее простую фигуру. Но, сначала посмотрим, как взаимодействует 3-х-мерный шар с 2-мерной вселенной, рис.А. Мы видим, что в этом случае образуется 2-мерная область — круг. В топологии доказано это свойство в общем случае: при пересечении объектов высшей размерности с пространством низшей, образованное сечение соответствует, по размерности, меньшей из них. Таким образом, если многомерный шар пересекаектся с пространством нашей Вселенной мы его будем воспринимать, как 3-х-мерный и его свойства будут зависеть от координат этого сечения в дополнительных измерениях. В тех случаях, когда шар не перемещается в этих дополнительных измерениях он будет проявляться в нашем мире, как стационарный 3-х-мерный объект. В противном случае, если шар пересекает наше пространство достаточно быстро, мы станем свидетелями необъяснимого и, даже, “чудесного” явления — в некоторой точке пространства, из “ниоткуда”, появляется маленький шарик, который непрерывно увеличивается, достигает максимального размера, затем уменьшается и исчезает. Эти рассуждения мы здесь провели для того, чтобы попытаться понять, каким образом могут проявляться в нашем пространстве многомерные объекты. В литературных источниках Ордена упоминается о существовании многомерных областей в центре Земли (размерность — 5) и Солнца (размерность — 10). Это действительно возможно, но только в том случае, если эти области стационарны относительно пространства нашей Вселенной. Основные параметры Солнечной системы, планет и самого Солнца практически неизменны на протяжении сотен миллионов лет, что подтверждается многочисленными палеонтологическими и астрономическими исследованиями. Однако, в некоторых областях Вселенной крупномасштабные многомерные объекты могут проявляться, как нестационарные. Эти явления могут сопровождаться гигантским выделением энергии. В ядрах некоторых галактик действительно наблюдаются такие процессы, причём, источник энергии очень компактен (по галактическим масштабам), а энергия соответствует миллионам звёзд. По некоторым признакам, в ядрах этих галактик происходит интенсивная генерация звёздного вещества. Современная наука пока не нашла удовлетворительного объяснения этим фактам. Одна из возможных гипотез может строится на основе упомянутых многомерных объектов. Кстати говоря, пресловутые “чёрные дыры”, играющие важную роль в современной астрофизике, изменяют метрику нашего пространства. Внутри этих объектов не существуют никакие структурные элементы, а, значит, размерность внуреннего пространства “дыры” равна 0. В области микромира можно также найти примеры объектов, свойства которых могут быть объяснены особенностями метрики нашего пространства. Многие слышали о “кварковой теории элементарных частиц”. В настоящее время она считается наиболее обоснованной и даёт предсказания, подтверждаемые экспериментом. Однако, сами кварки ни в одном из экспериментов не наблюдались. Теоретики “решили” эту проблему просто, они наделили кварки особым свойством “ненаблюдаемости отдельно” и назвали его “конфайментом”. Это свойство кварков может быть объяснено особенностями их метрики. Кварки, являясь 3-х-мерными частицами, могут иметь дополнительную степень свободы в 4-м измерении. Поэтому, в свободном состоянии они “развёрнуты” и не наблюдаются в нашем пространстве. При взаимодействии друг с другом 4-ое измерение компенсируется и их комбинация проявляется, как нормальная 3-х-мерная частица. В заключение этого раздела хочу привести шутливую поговорку физиков-теоретиков: “Хорощая” физическая теория должна использовать фундаментальные уравнения с метрикой не меньше 6-и. Кстати говоря, теория торсионных полей физика Шипова использует уравнения в 10-и-мерном пространстве и,видимо, является “хорошей”.

Практическое применение фракталов.

Сжатие изображений.

С помощью фракталов можно сжимать большие растровые изображения до долей их нормальных размеров. Этот утверждение следует из теоремы Банаха о сжимающих преобразованиях (также известной как Collage Theorem) и является результатом работы Майкла Барнсли исследователя Технологического института шт. Джорджия. Вкратце метод можно описать следующим образом. Изображение кодируется несколькими простыми преобразованиями (в нашем случае аффинными), т. е. коэффициентами этих преобразований (в нашем случае A,B,C,D,E,F). Например, закодировав какое-то изображение двумя аффинными преобразованиями, мы однозначно определяем его с помощью 12-ти коэффициентов. Если теперь задаться какой-либо начальной точкой (например, X=0 Y=0) и запустить итерационный процесс, то мы после первой итерации получим две точки, после второй — четыре, после третьей — восемь и т. д. Через несколько десятков итераций совокупность полученных точек будет описывать закодированное изображение. Но проблема состоит в том, что очень трудно найти коэффициенты преобразований, которые кодировали бы произвольное изображение. Несмотря на то, что было создано программное обеспечение, реализующее эти алгоритмы в библиотеках фрактального сжатия в Microsoft Encarta, достаточно эффективное решение не найдено до сих пор, а сам Майкл Барнсли продолжает упорно работать в выбранном направлении.

(Аффинное преобразование: Отображение f: Rⁿ → Rⁿ есть aффинное преобразование, если найдётся обратимая матрица M и вектор v Є Rⁿ такие, что f(x) = Mx + v.

(В этом определении вместо поля вещественных чисел R можно рассматривать произвольное поле)

Иначе говоря, преобразование называется аффинным, если его можно получить следующим образом:

1. Выбрать “новый” базис пространства с “новым” началом координат;

2. каждой точке x пространства поставить в соответстиве точку f(x), имеющую те же координаты относительно “новой” системы координат, что x в “старой”.

Свойства:

· При аффинном преобразовании прямая переходит в прямую.

· Более того, если размерность n>2, то любое преобразование пространства (т.е. биекция f: X ↔ Y пространства на себя), которое переводит прямые в прямые, является аффинным. Это определение используется в аксиоматическом построении аффинной геометрии.

· Частным случаем аффинных преобразований являются движения и преобразования подобия. (Подобие — преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A', B' имеет место соотношение | A'B' | = k | AB |, где k — положительное число, называемое коэффициентом подобия. Каждое движение (в том числе и тождественное) также можно рассматривать как преобразование подобия с коэффициентом k = 1.))

В настоящее время широко используются программы для генерации фрактальных изображений. В качестве примера можно привести Fractal Explorer — одна лучших на сегодняшний день программ для создания изображений фракталов; XaoS — многоплатформенный генератор фракталов, позволяет приближать и удалять картинку в реальном времени;

Генерация изображений природных объектов.

Рис.18. Фрактальное дерево.

Геометрические фракталы применяются для получения изображений деревьев, кустов, береговых линий и т. д. (Рис.18.) Алгебраические и стохастические — при построении ландшафтов, поверхности морей, карт, раскраски моделей биологических объектов и др. (Рис.19.).

Биология.

В биологии фракталы используются для моделирования популяций биологических объектов. Описания биосенсорных взаимодействий между особями. Моделирования процессов внутри организма, например, биения сердца, процессов кровообращения, структуры мозга.

Физика.

В физике фракталами хорошо описываются процессы, относящиеся к механике жидкостей и газов; моделирование пламени и плазмы; моделирование и изучение пористых материалов, в том числе в нефтехимии.

И в заключение: “Фракталы на марше”.

После формирования новой парадигмы произошел взрыв исследований по фрактальной физике. Одна из опубликованных книг отразила это даже в названии “Fractals Everywherec [7]. Фактически за короткий период была установлена экспериментально широкая распространенность фракталов в природе. Процессы и объекты фрактальной природы занимают от огромных масштабов, начиная с фрактального распределения вещества во вселенной, до самых малых масштабов, характеризующих флуктуации вакуума. Параллельно начались глубокие исследования по описанию свойств фракталов, механизмов их образования и наблюдаемых эффектов, связанных с ними. Концепция фракталов оказалась тесно связанной с еще одной физической областью — детерминированным хаосом [8, 9]. Взаимодействие этих областей обогатило эти две области как новыми объектами, (например, странными аттракторами, кантор-торами,) так и более глубоким пониманием процессов, протекающих в них. Возникли представления об обобщенном фрактальном броуновском движении, изменились представления об одной из самых сложных физических проблем — теории турбулентности. Здесь невозможно даже кратко перечислить все изменения, происшедшие в физике. Разумеется, фрактальная физика — еще очень молодая наука, и главные открытия еще ожидают нас впереди.

Интересно отметить исключительно быстрое проникновение фрактальной физики во многие прикладные области человеческой культуры. Для многих неизвестно, что при создании художественных фильмов уже достаточно давно используется концепция фракталов. Так, замечательные горные пейзажи, водопады и растительность во многих фантастических фильмах (например, “Звёздное переселение”) были созданы искусственно с помощью компьютерной графики. Множество самых современных и лучших программ для создания как двумерных, так и трёхмерных изображений используют идеологию фракталов. Это программы Bryse, Adobe Photoshop, Fractal Design Painter и много других. Созданные с их помощью, пейзажи вызывают полную иллюзию реальности и эстетическое удовольствие (рис. 19).

Рис.19. Пример трехмерного пейзажа.

Более того, фрактальность необходима даже для воспроизведения элементарного мазка кисти мастера, типа краски (акварель, масло, темпера или гуашь) и остальных атрибутов реальной живописи. Интересно отметить огромную заслугу в создании программы Bryce родоначальника фрактальной геометрии Мандельброта и его учеников. Большое число алгоритмов, используемых в этой программе, были разработаны именно ими еще до ее разработки. Собственно, один из учеников Мандельброта, защитивший диссертацию на соискание степени доктора философии в Йельском университете по теме “Методы формирования реалистичных изображений ландшафтов” (“Metods for Realistic Landscape Imaging”) в 1993 году, и начал впоследствии создание этой программы. Интуитивно роль фрактальности в природе чувствовали многие замечательные художники. Как это ни забавно, на их полотнах можно измерить фрактальную размерность изображенных объектов. Леонардо да Винчи даже сформулировал правило, которое на современном языке можно понять в рамках фрактальной идеологии. Он высказал предположение, что все ветки деревьев на данной высоте сложенные вместе совпадают по толщине с основным стволом, из которого они растут. Сейчас его наблюдение можно увязать с определением размерности ветвления.

Естественно, все сказанное о живописи можно перенести на музыку и воспроизведение или, точнее, имитацию звуков реальных людей, животных или музыкальных инструментов. Ясно, что тексты также должны обладать фрактальностью, например, была измерена фрактальная размерность текста библии. Очевидно новое направление анализа текстов, написанных на разных языках или разными людьми. Возникла новая идея фрактальной интерполяции. В свою очередь, это влечет использование фрактальности для создания новых принципов диагностики и прогнозирования сложных систем. Например таких, как финансовые рынки или биологические сообщества. Медицина также быстро отреагировала на новую парадигму, обнаружив фрактальность режимов работы головного мозга и сердечной деятельности, фрактальные органы – легкие и почки. Более того, интенсивно развивается синтез фрактальных органических соединений, обладающих совершенно уникальными свойствами и возможностями использования в биологии и медицине.

Таким образом, концепция фракталов становится не только частью “чистой” науки, но и элементом общечеловеческой культуры.

Литература

1. L. F. Richardson. The problem of contiguity: an appendix of statistics of deadly quarrels, General Systems Yearbook 6, p.139-187, 1961.

2. P. Meokin. Fractal aggregates and their fractal measures – In. Phase Transitions and Critical Phenomena, eds. C. Domb, J. L. Lebowitz, Academic Press, New York, 1987.

3. B. B. Mandelbrot. Fractals: Form, Chance and Dimension, W.H. Freeman, New San Francisko, 1977.

4. B. B. Mandelbrot. The fractal Geometry of Nature, Freeman, San Francisco, 1982.

5. Б. М. Смирнов. Проблема шаровой молнии. – М.: Наука,1988.

6. Е. Федер. Фракталы. – М.: Мир, 1991.

7. Michael Barsley. Fractals Everywhere, Acad. Press., Boston, 1988.

8. M. Шредер. Фракталы, хаос, степенные законы. – Ижевск: Удмуртский университет, 2000.

9. H.-O. Peityen, P. H. Richter. The Beauty of Fractals: Images of Complex Dynamical Systems. – Springer-Verlag, Berlin, 1986.

10. G. A. Edgar. Measure, Topology and Fractal Geometry, Springer-Verlag, New York, 1990.

Дата добавления: 2015-07-25