Исходные данные. По дисциплине прикладная механика

По дисциплине прикладная механика

на тему «Поршневой насос»

Вариант № 5

Студент: Устюгова О.А.

Группа: ОПИ-07

Преподаватель: Двинина Л.Б.

Екатеринбург

Содержание

С.

1. Исходные данные. 3

2. Структурный анализ механизма. 4

3. Кинематический анализ механизма. 6

3.1. План механизма в масштабе. 7

3.2. План скоростей. 9

3.3. План ускорений. 11

Список литературы.. 13

Исходные данные

Кинематическая схема поршневого насоса приведена на рис. 1.

Механизм состоит из кривошипа 1, шатунов 2, 3, 4 и ползуна (поршня) 5 диаметром d_п.

Рабочий ход поршня сверху вниз. Центры масс звеньев 2, 3, 4 находятся посередине их длин, звена 1 – в точке О, звена 2 – в точке D.

Исходные данные приведены в табл. 1.

Рис. 1. Поршневой насос

Таблица 1.

Частота вращения вала, n, об/мин	Геометрические размеры, мм
двигателя	кривошипа	a	b	c	OA	AB	AC	O1B	CD

2. Структурный анализ механизма

Под структурным анализом механизма понимается определение количества звеньев и кинематических пар, определение степени подвижности механизма (числа степеней свободы механизма) и установление класса механизма.

Структурным синтезом механизма называется проектирование структурной схемы механизма, которая состоит из не подвижного и подвижных звеньев и кинематических пар.

Определение числа свобод плоского механизма производится по формуле Чебышева:

S=3n - 2P₅ - 1P₄, где

n – количество звеньев;

P_k – число кинематических пар (k – номер класса).

Группой Ассура называется кинематическая цепь, которая в случае ее присоединения элементами внешних пар к стойке получает нулевую степень подвижности.

Механизм содержит пять подвижных звеньев (n=5) и шесть кинематических пар V класса.

P₄ = 0, т.к. механизм плоский

n = 5

P₅ = О – А – В – O₁ – С – D = 6

S = 3·5 - 2·6 = 6

Разложим механизм на группы Ассура:

1-я группа Ассура

2-я группа Ассура

3-я группа Ассура

3. Кинематический анализ механизма

Кинематический анализ механизмов состоит в определении закона движения звеньев по заданному движению ведущих звеньев.

Основные задачи кинематического анализа:

· определение крайних положений звеньев и траекторий движения их отдельных точек с целью построения плана механизма в масштабе;

· определение величин и направлений угловых и линейных скоростей с целью построения плана скоростей механизма;

· определение величин и направлений угловых и линейных ускорений с целью построения плана ускорений механизма.

Решение этих задач проводят двумя методами: аналитическим и графическим. Аналитический метод обладает высокой точностью, но трудоемкий. Более простым и наглядным методом кинематического анализа является графический метод, который широко применяется при предварительных расчетах механизма.

Масштабным называется безразмерная физическая величина, служащая для изображения звена или механизма в уменьшенном или увеличенном виде.

Масштабный коэффициент равен отношению заданной размерной величины к длине отрезка, изображающего эту величину на чертеже.

Различают:

· масштабный коэффициент длины ;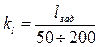

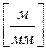· масштабный коэффициент скорости ;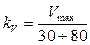

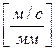· масштабный коэффициент ускорения .

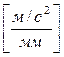
План механизма в масштабе

Масштабный коэффициент длины выбираем по условию, что длина самого большого звена в исходных данных (СD =1,420 м) не превышала 200 мм.

Примем масштаб 1:10.

СD =1,420 м = 1420 мм: 10 = 142 мм

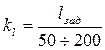
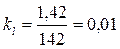
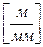
мм

мм

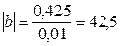мм

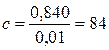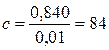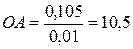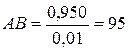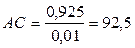мм

мм

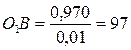мм

мм

мм

мм

На рис. 2 изобразим план механизма в масштабе

Рис. 2. План механизма в масштабе

Рис. 2.1. Варианты положения механизма

3.2. План скоростей

Построение начинаем с определения модуля скорости точки А начального звена 1:

,

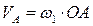где 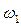‒ угловая скорость плоской фигуры, величина которой находится из формулы:

,

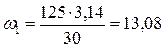рад/с

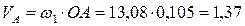м/с,

Изобразим вектор скорости 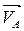из некоторой точки P_V, которая называется полюсом плана скоростей. Это вектор всегда направлен перпендикулярно начальному звену 1 в сторону его движения (план скоростей приведён на рис. 3).

В целях обеспечения требуемой точности построения длину этого вектора примем из интервала 30...80 мм, тогда масштабный коэффициент скорости равен:

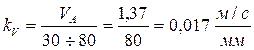
В конце вектора поставим стрелку и точку а. Скорость точки В определяем в соответствии с векторным уравнением:

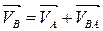
В силу того, что точка В принадлежит звену 3, совершающему вращательное движение вокруг точки O₁, вектор скорости 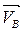направлен перпендикулярно звену 3. Кроме того, вектор 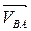перпендикулярен звену 2, и потому точку b на плане скоростей получим как точку пересечения перпендикуляров к направлениям звеньев 2 и 3 в расчётном положении, проведённых соответственно через точки а и P_V. Величину скорости точки В найдём, измерив длину отрезка P_Vb на плане скоростей и умножив её на масштаб:

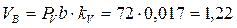м/с,

Угловая скорость звена 3 находится из формулы:

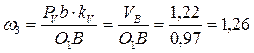рад/с

Для определения угловой скорости звена 2 необходима скорость V_BA во вращательном движении звена ВА вокруг полюса А разделить на длину этого звена:

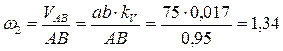рад/с

Составим пропорцию и найдем из нее отрезок ас.

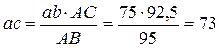мм

В силу того, что точка С и точка В принадлежат звену 2, совершающему вращательное движение вокруг точки А, вектор 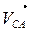направлен перпендикулярно звену 2 и скорость точки С будет находится по формуле:

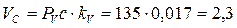м/с

Проводим из конца вектора 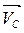прямую, перпендикулярную звену 4, а из полюса P_V ‒ прямую, параллельную направляющим ползуна 5, т.е. по вертикали. Точка пересечения этих прямых есть конец вектора 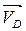, т.е. точка d. Модуль скорости точки d находится путём умножения длины отрезка P_Vd на масштабный коэффициент k_V:

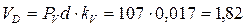м/с

Угловую скорость вращения звена 4 находим из формулы:

рад/с

Рис. 3. План скоростей

3.3. План ускорений

При построении плана ускорений принимаем, что ведущее звено 1 движется с постоянной угловой скоростью. В этом случае полное ускорение точки А к оси вращения звена ‒ точке О, а по величине определяется:

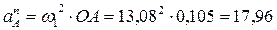м/с²

Перед началом построений выберем масштабный коэффициент, равный отношению ускорения к длине отрезка, изображающего эту величину. Для обеспечения требуемой точности построения длину отрезка принимают равной 80... 100 мм:

Изобразим вектор ускорения 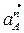из некоторой точки Р_а, которая называется полюсом плана ускорений. Этот вектор всегда направлен параллельно начальному звену 1 (рис. 4).

Примем длину этого вектора равной 100 мм, тогда масштабный коэффициент ускорения равен:

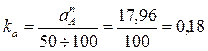
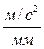
В конце вектора поставим стрелку и точку а.

Ускорение точки В находим в соответствии с векторной формулой:

,

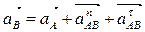При этом:

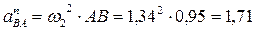м/с²

а вектор 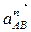направлен вдоль звена 2 от точки В к точке А. Длина вектора, изображающего это ускорение, равна величине этого ускорения, делённой на масштабный коэффициент:

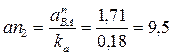мм

С другой стороны, точка В принадлежит звену 3, совершающему вращательное движение вокруг точки O₁. Следовательно, полное ускорение точки В равно сумме её нормальной и касательной составляющих:

,

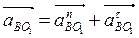причём по величине

м/с²

а направлен этот вектор вдоль O₁B от В к O₁. Длина вектора, изображающего это ускорение равна:

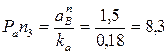мм

Из полюса плана ускорений проводим отрезок Р_аn₃ параллельно звену 3. Этот вектор изображает нормальное ускорение точки В. Из конца этого вектора проводим перпендикулярно ему линию, по которой направлена касательная составляющая ускорения точки В до пересечения с перпендикуляром к АВ (звено 2), проведённым из точки а. Полученную точку обозначим через b. Замерив длину отрезка Р_аb, находим полное ускорение точки В:

м/с²

Угловое ускорение звена 2 определяем после замера на чертеже длину вектора n₂b, изображающего касательную составляющую ускорения точки В:

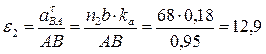рад/с²

Угловое ускорение звена 3 находим аналогично:

рад/с²

Составим пропорцию и найдем из неё отрезок ас.

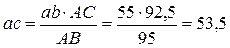мм

Ускорение точки с будет равно:

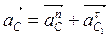
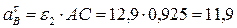м/с²

м/с²

Так как точка D принадлежит звену 5 (ползуну), то направление полного ускорения этой точки нам известно, оно параллельно направляющим ползуна. Следовательно, перпендикуляр к CD из точки с следует продолжать до пересечения с вертикальной прямой, проведённой из полюса плана ускорений. Отрезок cn₄ откладываем из точки с параллельно звену 5 в направлении от С к D. Перпендикулярно cn₄ проводим линию до пересечения с вертикальной линией, проведённой из полюса. Полученную точку обозначаем через d. Замеряем длину отрезка P_ad и находим полное ускорение точки D:

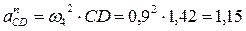м/с²

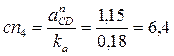мм

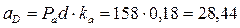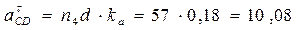м/с²

м/с²

Далее находим угловое ускорение звена 4:

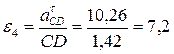рад/с²

Рис. 4. План ускорений

Список литературы

1. Артоболевский И.И. «Теория механизмов и машин» - М.: Наука, 1975.

2. Афанасьев А.И., Ляпцев С.А. «Курсовое проектирование по теории механизмов и машин» - УГГУ, 2000.

Дата добавления: 2015-07-25