Диаграмма деформации.

Приложенная к образцу нагрузка вызывает его деформацию. Соотношения между нагрузкой и деформацией описываются т. н. диаграммой деформации {рис. 3.5.). Вначале деформация образца (при растяжении — приращение длины Δl) пропорциональна возрастающей нагрузке Р, затем в точке п эта пропорциональность нарушается, однако для увеличения деформации необходимо дальнейшее повышение нагрузки Р; при Δl > Δl в деформация развивается без приложения усилия извне, при постепенно падающей нагрузке. Вид диаграммы деформации не меняется, если по оси ординат откладывать напряжение

σ = Р / F_o,

а по оси абсцисс — относительное удлинение

δ = Δl / l_o

(F_o и l_o — соответственно начальная площадь поперечного сечение и

расчётная длина образца).

Сопротивление материалов измеряется напряжениями, характеризующими нагрузку, приходящуюся на единицу площади поперечного сечения образца

σ =Р /F_o, , в кгс/мм2.

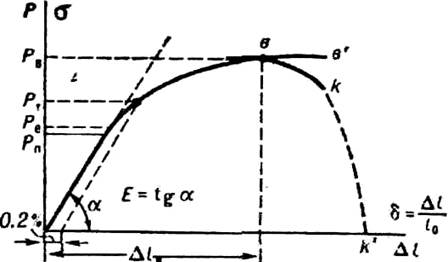
Рис. 3.5 Типичная диаграмма деформации при растяжении конструкционных материалов.

Упругие свойства и их основные параметры.

Напряжение σ_н = Р_н / F_o,(см. рис. 3.5), при котором нарушается пропорциональный нагрузке рост деформации, называется пределом пропорциональности. Этот параметр относится к важной характеристике упругих свойств материалов. При нагрузке Р < Рn разгрузка образца приводит к исчезновению деформации, возникшей в нём под действием приложенного усилия; такая деформация называется упругой. Небольшое превышение нагрузки относительно Р_n может не изменить характера деформации — она по-прежнему сохранит упругий характер.

Наибольшая нагрузка, которую выдерживает образец без появления остаточной пластической деформации при разгрузке, определяет предел упругости материала:

σ_{l =} P_l / F_o. - Этот параметр также относится к основным характеристикам упругих свойств материалов (см. рис. 3.5).

У конструкционных неметаллических материалов (пластмассы, резины) приложенная нагрузка может вызвать упругую, высокоэластическую и остаточную деформации. В отличие от упругой, высокоэластическая деформация исчезает не сразу после разгрузки, а с течением времени. Высокопрочные армированные полимеры (стеклопластики, углепластики и др.) разрушаются при удлинении 1—3%. На последних стадиях нагружения у некоторых армированных полимеров появляется высокоэластическая деформация. Высокоэластический модуль ниже модуля упругости, поэтому диаграмма деформации в этом случае имеет тенденцию отклоняться к оси абсцисс.

В упругой области напряжение и деформация связаны коэффициентом пропорциональности. При растяжении σ = Еδ, где Е — т. н. модуль нормальной упругости, численно равный тангенсу угла наклона прямолинейного участка кривой σ = σ (δ) к оси деформации (рис. 3.5.). При испытании на растяжение цилиндрического или плоского образца одноосному (σ₁>0; (σ ₂ = σ ₃ = 0) напряжённому состоянию соответствует трёхосное деформированное состояние (приращение длины в направлении действия приложенных сил и уменьшение линейных размеров в двух других взаимно перпендикулярных направлениях): δ₁ > 0; δ₂ = δ₃ < 0.

Соотношение между поперечной и продольной деформацией (коэффициент Пуассона)

μ = δ₂/δ₁

в пределах упругости для основных конструкционных материалов колеблется в довольно узких пределах (0,27—0,3 для сталей, 0,3- 0,33 для алюминиевых сплавов). Коэффициент Пуассона является одной из основных расчётных характеристик. Зная μ и Е, можно расчётным путём определить и модуль сдвига

G = E / 2(1+ μ )

и модуль объёмной упругости

К = Е / 3(1-2 μ).

Для определения Е, G, и μ пользуются тензометрами.

Модули упругости, величины, характеризующие упругие свойства материала. В случае малых деформаций, когда справедлив закон Гука, т. е. имеет место линейная зависимость между напряжениями и деформациями, модули упругости (М. у.) представляют собой коэффициент пропорциональности в этих соотношениях.

Одностороннему нормальному напряжению σ, возникающему при простом растяжении (сжатии), соответствует в направлении растяжения модуль продольной упругости_Е _ (модуль Юнга). Он равен отношению нормального напряжения σ к относительному удлинению ε, вызванному этим напряжением в направлении его действия:

Е = σ / ε, и характеризует способность материала сопротивляться растяжению.

Напряжённому состоянию чистого сдвига, при котором по двум взаимно перпендикулярным площадкам действуют только касательные напряжения τ, соответствует модуль сдвига G. Модуль сдвига равен отношению касательного напряжения τ к величине угла сдвига у, определяющего искажение прямого угла между плоскостями, по которым действуют касательные напряжения, т. е, G τ = τ / у. Модуль сдвига определяет способность материала сопротивляться изменению формы при сохранении его объёма.

Всестороннему нормальному напряжению σ, одинаковому по всем направлениям (возникающему, например, при гидростатическом давлении), соответствует модуль объёмного сжатия К — объёмный модуль упругости. Он равен отношению величины нормального напряжения σ к величине относительного объёмного сжатия Δ, вызванного этим напряжением: К = σ / Δ. Объёмный модуль упругости характеризует способность материала сопротивляться изменению его объёма, не сопровождающемуся изменением формы.

К постоянным величинам, характеризующим упругие свойства материала, относится также Пуассона коэффициент v. Величина его равна отношению абсолютному значения относительного поперечного сжатия сечения ε' (при одностороннем растяжении) к относительному продольному удлинению ε, т. е. v = | ε ' |/ ε.

В случае однородного изотропного тела модули упругости одинаковы по всем направлениям. Четыре постоянные величины Е, G, К и v связаны между собой двумя соотношениями:

G = E / 2(1+ v), K = E / 3(1-2 v).

Следовательно, только две из них являются независимыми величинами и упругие свойства изотропного тела определяются двумя упругими постоянными. В случае анизотропного материала постоянные Е, G и v принимают различные значения в различных направлениях и величины их могут изменяться в широких пределах. Количество М. у. анизотропного материала зависит от структуры материала. Анизотропное тело, лишённое всякой симметрии в отношении упругих свойств, имеет 21 М. у. При наличии симметрии в материале число М. у. сокращается.

М. у. устанавливаются экспериментально-механическим испытанием образцов изучаемых материалов. М. у. не являются строго постоянными величинами для одного и того же материала, их значения меняются в зависимости от химического состава материала, от его предварительной обработки (термическая обработка, прокат, ковка и др.). Значения М. у. также зависят от температуры материала.

Дата добавления: 2015-07-25