Розрахунок зубців на міцність при згинанні

Зуб навантажений біля вершини питомою нормальною силою

(4.17)

де - нормальна сила в зачепленні,

- коефіцієнт навантаження.

Питома кружна сила

(4.18)

(4.19)

Переносимо силу вздовж лінії її дії по осі зубця і розкладаємо на дві складові:

згинаючу

та стискаючу .

Напруження в небезпечному перетині зубця (розрахунок виконується для розтягненої сторони зубця, так як утомні тріщини з’являються на ній)

(4.20)

де - момент опору згину небезпечного перетину шириною рівною одиниці

товщина зубця в небезпечному перетині,

- площа одиниці довжини небезпечного перетину;

- розрахункове плече сили (згинаючої);

теоретичний коефіцієнт концентрації напружень.

Підставляючи в (4.20) значення , , виносимо за дужки один спільний множник та помножуємо чисельник і знаменник на . Остаточно згинаюче напруження в небезпечному перетині та умови міцності зубців при згинанні

(4.21)

де

- кружна сила ділильному циліндрі в торцевому перерізі;

b - ширина вінця зубчастого колеса;

- нормальний модуль.

- коефіцієнт, яким враховують форму зубця і концентрацію напружень

;

- коефіцієнт, яким враховують вплив нахилу зубця;

- коефіцієнт, яким враховують вплив перекриття зубців;

- коефіцієнт, яким враховують зовнішнє динамічне навантаження (невраховане в циклограмі навантаження);

- коефіцієнт, яким враховують внутрішнє динамічне навантаження;

- коефіцієнт, яким враховують нерівномірність розподілу навантаження по довжині контактних ліній;

- коефіцієнт, яким враховують розподіл навантаження між зубцями.

Допустиме напруження згину на перехідній поверхні зубця, яке не викликає утомного руйнування матеріалу

(4.22)

де межа витривалості зубців при згині, яка відповідає базовому числу циклів напружень;

- мінімальний коефіцієнт запасу міцності;

- коефіцієнт довговічності;

- коефіцієнт, яким враховують вплив шорсткості перехідної поверхні;

- коефіцієнт, яким враховують розмір зубчастого колеса;

- опорний коефіцієнт, враховує чутливість матеріалу до концентрації напружень.

Допустиме напруження згину в небезпечному перетині, яке не викликає залишкових деформацій, крихкого зламу або первинних тріщин.

(4.23)

де - граничне напруження згину при максимальному навантаженні,

(4.24)

- межа витривалості зубців при згині;

- мінімальний коефіцієнт запасу міцності при розрахунку по максимальних навантаженнях;

- максимальне значення коефіцієнта довговічності;

- опорний коефіцієнт при максимальному навантаженні;

- опорний коефіцієнт випробуваного зубчастого колеса при максимальному навантаженні.

Навантажувальна здатність зубця при згині забезпечується при виниканні умов будь-якого з критеріїв:

- напруження (4.25-4.26)

тут максимальне місцеве напруження від згину в небезпечному перетині зубця за весь термін служби;

- безпека (4.27)

(4.28)

тут - розрахунковий коефіцієнт запасу міцності для попередження утомного руйнування матеріалу

S_FSt – розрахунковий коефіцієнт запасу міцності для попередження залишкових деформацій, крихкого зламу або первинних тріщин при максимальному навантаженні

- ресурс N_L ≥ N_K, (4.29)

σ_Fmax ≤ σ_FPmax (4.30)

N_L - число циклів напружень у відповідності з розрахунковим строком служби;

N_K – число циклів напружень у відповідності з заданим строком служби;

- імовірність безвідмовної (4.31)

роботи (4.32)

де - імовірність відсутності пошкоджень протягом заданого строку служби;

мінімальне розгламентоване значення ;

- імовірність відсутності крихкого зламу або залишкових деформацій при максимальному навантажені;

- мінімальне розгламентоване значення .

Проектний розрахунок

Орієнтовне значення модуля при заданому параметрі

(4.33)

де K_m – допоміжний коефіцієнт:

= 14- для прямозубих передач;

= 11,2 - для косозубих ( та шевронних;

= 12,5 – для косозубих (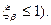

Орієнтовне значення модуля при заданій міжосьовій відстані

(4.34)

де - допоміжний коефіцієнт:

= 1400 - для прямозубих передач;

= 1100 - для косозубих (

= 850 - для косозубих ( і шевронних.

4.6 Передачі конічними зубчастими колесам и

Застосовуються в передачах між валами, осі яких розміщені (перетиняються) під кутом (переважно 90⁰).

Конічні колеса виготовляють з прямими, тангенційними, та круговими зубцями.

Прямозубі колеса найбільш прості у виготовлені та монтажі, але мають відносно невисоку навантажувальну здатність. Застосовуються при швидкостях(кружних) (

Колеса з круговими зубцями мають значно більшу несучу (навантажувальну) здатність; більшу плавність у роботі, створюють менше шуму.

Геометричні параметри конічних зубчастих предач.

Зубці конічних коліс утворюються обкаткою по плоскому колесу з прямолінійним профілем зубців, аналогічно тому, як зубці циліндричних коліс утворюються обкаткою по рейці.

Число зубців плоского колеса .

Замість початкових та ділильних циліндрів в циліндричних колесах в конічних вводяться поняття початковий і ділильний корпуси, які як правило співпадають, так як для конічних коліс кутову корекцію практично не застосовують.

В якості торцових перерізів розглядаються перерізи поверхневих додаткових конусів, тобто конусів, осі яких співпадають з осями коліс, а твірні перпендикулярні до твірних ділильних конусів.

Зовнішні ділильні діаметри

(4.35)

кути ділильних конусів

, (4.36)

Зовнішня конусна відстань

(4.37)

Ширина зубчастого вінця

(4.38)

Середня конусна відстань

(4.39)

Середній коловий модуль

(4.40)

Середній ділильний діаметр

(4.41)

Зовнішня висота зуба

(4.42)

Зовнішня висота головки зуба

(4.43)

Зовнішній діаметр вершини зубців

, (4.44)

Кут ніжки зуба

, (4.45)

Кут головки зуба

(4.46)

Кут конуса вершини

(4.47)

Кут конуса западин

(4.48)

Сили в зачепленнях конічних зубчастих коліс

Кружна (тангенційна) сила, віднесена до середнього по ширині вінця ділильного кола діаметром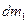

(4.49)

Прямозубі конічні колеса

Як уже зазначалось, в конічних передачах з прямими і не прямими зубцями не застосовується кутова проекція (нерівнозміщене зачеплення коліс), відтак в них кут зачеплення дорівнює куту профілю ріжучого інструменту

В площині діє сила , яка розсовує колеса. По аналогії з циліндричними колесами

(4.50)

Проекції сил на осі у і z

, (4.51)

(4.52)

тут - кут початкового конуса.

Сумарна, нормальна до осі вала сила, розміщується в площині 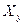(4.53)

Конічні колеса з тангенційними і криволінійними зубцями

1-й розрахунковий випадок: нормальна до лінії зубця сила , розміщена в площині дотичній до ділильного конуса, має проекцію на твірну ділильного конуса спрямовану від його вершини.

(4.54)

Сила, яка розсовує зубці коліс, нормальна до твірної ділильного конуса

(4.55)

Складова сили спрямована вздовж твірної ділильного конуса

(4.56)

Сили, діючі вздовж осі y і z визначаються як алгебраїчна сума проекцій сил і 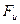на ці осі

(4.57)

(4.58)

2-й розрахунковий випадок: нормальна до лінії зубця сила має проекцію на твірну початкового конуса спрямованого до його вершини. В зв’язку з цим у формулах (4.42) і (4.43) знаки в дужках змінюються на протилежні. Спрямування осьової сили до вершини конуса небажане в зв’язку з можливістю заклинювання передачі при значних осьових зазорах в підшипниках. Нескладно уявити, що при ∑ = δ₁ + δ₂ = 90⁰ радіальна сила на шестерні по величині дорівнюватиме осьовій силі на колесі, а осьова сила на шестерні, відповідно радіальній силі на колесі.

При визначенні сил, діючих на вали і осі з урахуванням сил тертя вихідним є положення про те, що сумарна сила взаємодіє між зубцями нахилена в площині ковзання під кутом тертя відносно спільної нормалі до поверхонь зубців. Можна використати формулу із збільшеними на величину кутів тертя кутами зачеплення.

Розрахунок конічних зубчастих коліс на міцність

Розрахунки зводяться до еквівалентних циліндричних коліс. Розрахункове навантаження приймається рівним силі, віднесеній до середнього по ширині вінця ділильного кола конічних коліс

; ; (4.59)

тут ;

Діаметри еквівалентних циліндричних прямозубих коліс

(4.60)

Число зубців еквівалентних циліндричних прямозубих коліс

(4.61)

Еквівалентне передаточне число

(4.62)

Розрахунок на контактну міцність

o - в формулу для розрахунку контактних напружень в циліндричних колесах, записану через підставляють

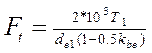(4.63)

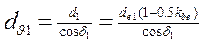, замість підставляють , замість U→U_υ = (, вираз 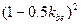залишають наближено .

Крім цього в формулу вводиться встановлений дослідним шляхом коефіцієнт зменшення несучої здатності конічних передач в порівнянні з еквівалентними циліндричними .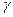

Остаточно формула для визначення контактних напружень

(4.64)

де

або (4.65)

де

Перевірка міцності при згинанні

(4.66)

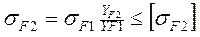(4.67)

Для випадку, коли основним критерієм являється міцність при згинанні і числа зубців задані наперед

. (4.68)

Дата добавления: 2015-07-25