Примечание. Отметим, что в системе можно опустить одно из двух условий: или

Отметим, что в системе можно опустить одно из двух условий: или , или (что мы и будем иногда делать в дальнейшем). Действительно, если для некоторого числа х ₀ справедливо равенство α (x ₀) = β (x ₀) и одно из условий, например , то тогда справедливо и второе условие , так как α (x ₀) = β (x ₀).

На слайде приведен пример применения ут­верждений 1 и 2.

Задача 4. Решить уравнение

87cos(x ²) + (8 – 6 x)⁴ = x ⁸ + 87cos(8 – 6 x).

Решение. Приведем исходное уравнение к виду

x ⁸ – 87cos(x ²) = (8 – 6 x)⁴ – 87cos(8 – 6 x).

Рассмотрим непрерывную функцию f (t) = t ⁴ – 87cos t. Данная функция определена для любого значения аргумента, четная, т.к. f(– t) = f (t). Найдем ее производную: .

При : , а при :

.

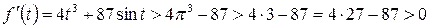Таким образом, при , следовательно, f (t) возрастает на промежутке . Значит, каждое свое значение из множества значения E(f), кроме f (0), функция принимает в двух симметричных относительно t = 0 точках, а стало быть, уравнение f (t ₁) = f (t ₂) равносильно уравнению 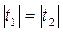. Записав исходное уравнение в виде f(x²)=f(8-6x), получим

Ответ. , , , .

Дата добавления: 2015-07-25