Сделать схематический чертеж.

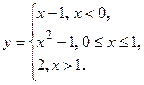
Решение. Функция 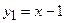непрерывна для 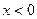, функция 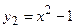непрерывна в каждой точке из 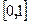, функция 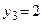непрерывна в каждой точке интервала .

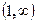Точки, в которых функция может иметь разрыв, это точк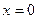и и 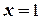, где функция меняет свое аналитическое выражение.

Исследуем точку .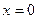

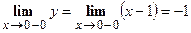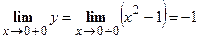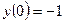, , . Таким образом, точка 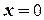есть точка непрерывности функции .

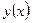Исследуем точку .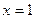

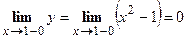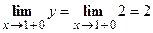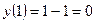, , . Таким образом, односторонние пределы существуют, конечны, но не равны между собой. По определению, исследуемая точка – точка разрыва первого рода. Величина скачка функции в точке разрыва 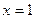равен .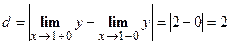

Сделаем схематический чертеж

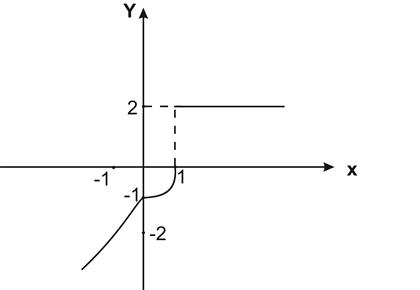
Рис. 2

Дата добавления: 2015-07-25