Задание {{ 278 }} ТЗ № 164

Уравнение плоскости, проходящей через точку М(2; 3; -1) и параллельную плоскости 5x - 3у + 2z - 10 = 0 имеет вид:

R 5x - 3у + 2z + 1 = 0

£ 5x - 3у + 2z - 1 = 0

£ 10x - 6у + 4z - 10 = 0

£ 10x - 6у + 4z - 20 = 0

Задание {{ 279 }} ТЗ № 166

Расстояние от точки М(5; 1; -1) до плоскости х - 2у - 2 z + 4 = 0 равно:

R 3

£ 4

£ 9

£ 17,6

Задание {{ 280 }} ТЗ № 167

Расстояние от точки М(1; 3; -2) до плоскости 2х - 3у - 4 z + 28 = 0 равно:

£ 3

£ 4

R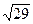

£ 17,6

Задание {{ 281 }} ТЗ № 281

Нормальный вектор к прямой х - 3 у - 13 =0 имеет координаты:

R N = (1; -3)

£ N = (-3; -13)

£ N = (1; -13)

£ N = (1; -16)

Задание {{ 282 }} ТЗ № 282

Уравнение плоскости, проходящей через точки М1(1; 2; 3), М2(2; 0; -7), М3(1; 1; 1), имеет вид:

R +: 6x - 2у + z - 5 = 0

£ 2x + у - z + 1 = 0

£ 5x + 4у + z - 3 = 0

£ 6x - 4у + 5z + 3 = 0

Дата добавления: 2015-07-25