
Читайте также:
|
Возьмем несложную задачу, на примере которой будем обсуждать вопросы структурирования.
Задача. Значение наибольшего из трех чисел a,b,c присвоить переменной М.
В первом варианте решения будем использовать для определения максимума только парные сравнения исходных чисел. Блок-схема решения показана на рис. 3. Такое решение позволяет всегда получить ответ с помощью ровно двух сравнений и одного присваивания.
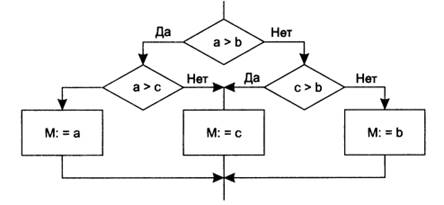
Рис. 3. Неструктурированное решение задачи определения максимума из трех чисел
Вначале сравниваются a и b. Если a>b, то претендентами на максимум остаются а и с, и максимум окончательно определяется из сравнения a > c. Если a не больше b, то максимум находится из сравнения b и c.
Как видно из рис. 3, схема нашего решения не является композицией типовых структур. Раз так, запишем ее решение на Паскале с помощью goto. И уж если мы пока не можем обойтись в этой ситуации без переходов, пусть это будет примером того, как не надо программировать (листинг 2). Я запутал текст несколько больше обычного, хотя это не совсем беспорядочное программирование.
Некоторый принцип все же применялся. Вначале были записаны по порядку три действия,
которые присваивают значение величине М, ведь именно одно из них мы все равно должны будем выполнить. Затем, двигаясь от трех этих действий, как от фундамента (снизу вверх по схеме), записал условия. Потом предусмотрел недостающие переходы.
Листинг 2. Так делать не надо!
goto 7;
2: М:= a; goto 1;
Структурное программирование 71
3: М:= с; goto l;
4: М:= b; goto 1;
5: if a>c then goto 2 else goto 3;
6: if Ob then goto 3 else goto 4;
7: if a>b then goto 5 else goto 6;
1:
Получилась еще одна порция спагетти.
Теорема структурирования
В статье, опубликованной в 1966 году, итальянские математики Коррадо Бём (Corrado Bohm) и Джузеппе Якопини (Guiseppe Jacopini) доказали, что любой алгоритм можно представить с помощью только двух базовых структур. Этот результат и носит название теоремы структурирования. Доказательство Бёма и Якопини конструктивно, то есть не только устанавливает саму возможность сведения алгоритма к двум базовым структурам, но и дает способ такого преобразования. Мы используем несколько иной вариант доказательства — преобразование Ашкрофта-Манны (Е. Aschkroft, Z. Manna).
Теорема. Для любой программы, выраженной блок-схемой с одним входом и одним выходом, можно построить эквивалентную программу, то есть выполняющую те же преобразования исходных данных в результаты с помощью тех же вычислений, единственными управляющими структурами в которой являются цепочка и цикл с предусловием.
Покажем вначале, что структуру «ветвление» можно представить с помощью цепочки и цикла с предусловием. Запишем ветвление в общем виде:
if В then S1 else S2
Здесь в — логическое выражение (условие); s1 и S2 — операторы. Построим программу, эквивалентную этой конструкции, но использующую только цепочку (следование операторов друг за другом) и цикл while. Используем вспомогательные логические переменные S1 и S2 (будем считать, что таких переменных нет в - исходной программе).
b1:= В; b2:= true;
while b1 do begin
S1; b1:= false; b2:= false;
end;
while b2 do begin
S2; b2:= false;
end;
Нетрудно убедиться, что эта программа выполняет те же действия и проверки и в том же порядке, что и исходная, оперируя также со вспомогательными переменными. Действительно, условие в вычисляется один раз, как и в исходной программе, до выполнения S1 либо S2. Если B истинно, то выполняется первый цикл while один раз (поскольку bl внутри цикла получает значение false), а в нем оператор S1. При этом Ь2 становится равным false и поэтому второй цикл не выполняется. Если B — ложь, то b1 — тоже ложь, первый цикл не выполняется, но, поскольку b2 в этом случае сохраняет значение true, выполняется ровно один раз второй цикл, а в нем S2.
Понятно, что такая замена бессмысленна на практике, а имеет только теоретическое значение.
Продолжим доказательство, формулируя алгоритм преобразования исходной блок-схемы в эквивалентную структурированную программу. Для иллюстрации алгоритма будем использовать схему из рассмотренного примера о нахождении максимума из трех чисел (см. рис. 3).
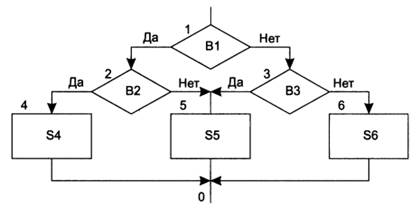
Рис. 4. Структурирование алгоритма нахождения максимума из трех чисел
Эта программа выполняет те же действия и те же проверки в том же порядке, что и исходная, то есть эквивалентна ей. Программа построена с помощью следования, цикла с предусловием, развилки и многозначного ветвления. Многозначное ветвление может быть заменено вложенными if - then - else, а эти конструкции, как было показано выше, могут быть заменены цепочками и циклами while. После таких замен получится программа, состоящая только из цепочек и циклов с предусловием. Что и требовалось доказать.
Полученная эквивалентная программа, особенно если сделать подстановки вместо case и if - then - else, получается очень громоздкой и, хотя является структурированной, но, пожалуй, даже менее понятна, чем программа из листинга 2.
Чтобы получить практически полезный результат, то есть решить исходную задачу нахождения максимума трех чисел с помощью структурированной и несложной программы, продолжим преобразования для нашего примера.
Заменим в программе присваивания L: = 4,L: = 5 и L:= 6 на действия, выполняющиеся на следующем витке цикла при соответствующем значении L (помеченные этим значением l). Поскольку L больше не может принять значения 4,5 и 6, то соответствующие ветви в case больше не нужны. Получим:
L:= 1;
while L<>0 do
case L of
1: if Bl then L:= 2 else L:= 3;
2: if B2 then begin S4; L:= 0 end
else begin S5; L:= 0 end;
3: if B3 then begin S5; L:= 0 end
else begin S6; L:= 0 end;
end
Аналогичную замену выполним теперь для L:- 2иъ:= 3. Получим:
L:= 1;
while LoO do
case L of
1: if Bl then
if B2 then begin S4; L:= 0 end
else begin S5; L:= 0 end
else
if B3 then begin S5; L:=-- 0 end
else begin S6; L: = 0 end;
end
Теперь остался только один вариант в операторе case, а значит, сам этот оператор больше не нужен, поскольку никакого значения, отличного от 1, счетчик при входе в цикл принять не может. После выполнения этого единственного варианта счетчик всегда принимает значение 0, а значит, цикл выполняется ровно один раз, и тоже больше не нужен. Не требуется и сам счетчик. Окончательно имеем:
if Bl then
if B2 then S4
else S5
else
if B3 then S5
else S6
После подстановки вместо S и B соответствующих действий и условий исходной задачи получаем ее структурированное и вполне приемлемое решение:
if a>b then
if a>c then M:= a
else M:= с
else
if Ob then M:= с
else M:= b
Конечно, так можно было записать и не прибегая к громоздким формальным преобразованиям. Достаточно было заметить, что, дублируя блок 5 (м: = с), мы превращаем схему в композицию трех развилок.
Продемонстрированное преобразование не может, конечно же, рассматриваться как прием для практической работы: создали алгоритм «как попало», а потом преобразовали в структурированную форму. Нужно стремиться с самого начала при разработке программы мыслить структурно. При использовании современных языков это несложно. Доказанная же теорема позволяет нам быть уверенными, что структурное решение всегда существует.
Хочу также подчеркнуть, что структурный подход отнюдь не гарантирует получения наилучших решений поставленных задач. Ничто не заменит изобретательности, интуиции, фундаментальной подготовки. Структурное программирование лишь позволяет выразить уже найденный алгоритм в ясной форме. Вернемся к нашей задаче о поиске максимума трех чисел. Ее решение может быть и другим. Снимая ограничение на допустимость только одиночных сравнений, можем записать:
if (a>b) and (a>c) then
M:= a
else if b>c then
M:= b
else
M:= с
Стилистически это решение, безусловно, лучше предыдущего: короче и понятней. А если действует короткая схема вычисления логических выражений, то и число сравнений всегда равно двум, как в предыдущем случае. А вот еще вариант:
М:= а;
if b>M then M:= b;
if ОМ then M:= с;
Здесь использован совсем другой подход к задаче. И никакое структурное программирование найти такой подход не помогает. Хотя в этом варианте может потребоваться больше одного присваивания, зато подобный способ решения, в отличие от предыдущих, легко обобщается на случай произвольного числа переменных.
Пошаговая детализация
Мы рассмотрели структурное программирование в его собственном смысле — программирование на основе стандартных управляющих структур. Но этот термин очень часто употребляется более широко, обозначая весь комплекс технологических приемов, сформировавшихся в конце 1960-х -- начале 1970-х годов. К числу таких приемов относится и метод пошаговой детализации при разработке программ.
Суть этого метода состоит в том, что, приступая к решению задачи, ее вначале рассматривают как некое единое действие. Затем выделяют в задаче небольшое число подзадач и устанавливают характер их взаимодействия. Далее каждая подзадача разбивается снова на несколько подзадач, и так до тех пор, пока выделенные подзадачи не смогут быть решены непосредственно. При разбиении па подзадачи обычно руководствуются правилом «7±2», разделяя каждую задачу примерно на 5-9 частей. Считается, что именно таким количеством элементов человек может свободно оперировать, не утрачивая контроля над их взаимодействием. Уже после первых шагов детализации может быть записана программа и начата ее отладка. Нереализованные части программы временно заменяются «заглушками», которые обеспечивают некоторый минимум действий вместо той части, которую замещают.
Структурное программирование служит теоретической базой метода пошаговой детализации, гарантируя, что процесс детализации всегда возможен. Действительно, на первом шаге задача предстает как один функциональный блок (рис. 5).
Далее этот блок может быть представлен как одна из базовых структур, содержащая в свою очередь несколько блоков. Каждый функциональный блок этой структуры вновь может быть представлен как одна из типовых структур. И так далее, до тех пор, пока все получившиеся функциональные блоки не будут реализовываться с помощью отдельных операторов выбранного языка программирования.
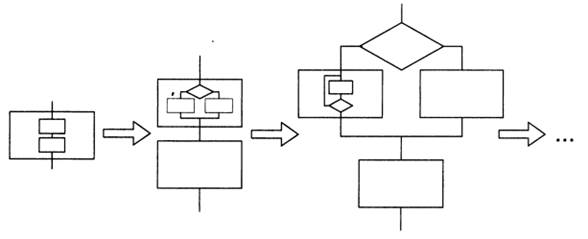
Рис. 5. Пошаговая детализация
Можно даже предложить универсальный алгоритм решения любой задачи (больше в шутку, но и всерьез):
Нарисуй прямоугольник и обозначь выполняемое им действие;
while есть прямоугольник, действие которого
не является простым
do begin
Выбери на рис. 1 подходящую структуру,
подставь ее вместо прямоугольника и
обозначь условия и действия ее блоков
end;
{ Задача решена }
Буквальное применение такого приема — замена на каждом шаге детализации функционального блока ровно на одну структуру — непрактично. Получается слишком много слишком мелких шагов. Это лишь предельный случай, непосредственно следующий из идеи структурного программирования. На практике при детализации лучше применять правило «7±2».
Совсем не обязательно пользоваться блок-схемами при разработке программ с помощью пошаговой детализации. Наоборот, унификация стиля и достаточная выразительность структурных управляющих операторов, небольшое число подзадач, выделяемых на каждом шаге, делают блок-схемы ненужными. Они уже не дают большей наглядности, чем обеспечивает хорошо структурированная программа.
Пошаговая детализация имеет и другие названия. В статье «Разработка программ пошаговым усовершенствованием», опубликованной в 1971 году, Н. Вирт, вероятно, впервые вводит подобный термин. Называют такой подход также нисходящим проектированием, разработкой по методу «сверху вниз» и т. д.
Дата добавления: 2015-07-25; просмотров: 88 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теплофізичні властивості будівельних матеріалів. | | | Структурные подразделения УФМС России по Омской области |