С>0 nÎN |xn|£C

Рассмотрим >0, для него:

$N₂ÎN "nÎN (n>N₂)Þ(|x_n-a|< )

Положим N=max{N₁;N₂}

Рассмотрим произвольное n>N:

||

Вывод:

"e>0 $NÎN: "nÎN, (n>N)Þ(|x_ny_n-ab|<e)

8° Если последовательности {x_n} и {y_n} сходятся к a и b, то последовательность { } сходиться, причем к .

Доказательство:

I. Докажем что { } сходится к 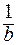при дополнительном условии, что "nÎN y_n¹0:

Рассмотрим e>0 и рассмотрим >0, для него найдем:

$N₁ÎN: "nÎN, (n>N₁)Þ(|y_n-b|<e)

Так как y_n®b, то по свойству 4° |y_n|®|b|.

Так как |b|>| |, поэтому по свойству 3°:

$N­₂ÎN: "nÎN, (n>N₂)Þ(|yn|>| |)

Положим N=max{N₁;N₂}

Рассмотрим произвольное n>N:

"e>0 $NÎN: "nÎN, (n>N)Þ().

II. Докажем что Þ по свойству 7° получаем что, { } ® .

Дата добавления: 2015-07-25