N>n2þzn<a-e

N0>N1)Þ(xn0>).

N0>N2)Þ(yn0<).

В итоге получаем противоречие x_n0>y_n0, а значит а<b.

2° Если для трех последовательностей {x_n}, {y_n} и {z_n} выполняются свойства:

1) "nÎN x_n£y_n£z_n

2) {x_n} и {y_n} сходятся к одному пределу а, то {y_n} также сходится к пределу а.

Доказательство:

т.a – предел последовательности x_n:

"e>0 $N₁ÎN: "nÎN, (n>N₁)Þ(|x_n-a|<e)

т.a – предел последовательности z_n:

"e>0 $N₂ÎN: "nÎN, (n>N₂)Þ(|z_n-a|<e)

Положим N=max{N₁;N₂}.

Если рассмотрим n>N:

n>N₁Þx_n>a+e

n>N2Þzn<a-e

Следовательно: a-e £ x_n £ y_n £ z_n £ a+e;

Значит (a-e<y_n<a+e)Þy_nÎO_e(a)

В итоге:

"e>0 $NÎN "nÎN (n>N)Þ(ynÎO_e(a)), т.е. т.a – предел последовательности y_n.

3° Если последовательность {x_n} сходиться к т. а, причем a>b то:

$NÎN, "nÎN (n>N)Þ(x_n>b)

Доказательство:

Рассмотрим e=a-b>0, для него найдем N:

"nÎN (n>N)Þ(x_nÎOe(a))

Так как x_nÎO_e(a), то x­_n>a-e=a-(a-b)=bÞx_n>b.

4° Если последовательность {x_n} сходиться к т. а, то последовательность {|x_n|} сходиться к |a|.

Доказательство:

По лемме что: ||a|-|b||£|a-b|, следует что: ||x_n|-|a||=|x_n-a|.

т.а – предел последовательности xn:

"e>0 $NÎN: "nÎN, (n>N)Þ(|x_n-a|<e)

т.|a| – предел последовательности |x_n|

"e>0 $NÎN: "nÎN, (n>N)Þ(||x_n­|-|a||<e)

Зафиксировав произвольный e>0 и найдя для него N из этого уравнения мы можем утверждаться что:

"nÎN, (n>N)Þ(||x_n|-|a||<e)

5° Если {x_n} и {y_n} соответственно сходятся к a и b, то последовательность {x_n+y_n}, сходиться к a+b.

Доказательство:

Зафиксируем e>0;

Рассмотрим >0; Для него из определения того что x_n®a найдем:

N₁ÎN: "nÎN, (n>N₁)Þ(|x_n-a|< )

Для >0, из определения того что y_n®b, найдем:

N₂ÎN: "nÎN, (n>N)Þ(|y_n-a|< )

Положим N=max{N₁;N₂}

Возьмем произвольное n>N:

|(x_n+y_n)-(a+b)|=|(x_n-a)+(y_n-b)|£ |x_n-a|+|y_n-b|< + ;

Вывод:

"e>0 $NÎN: "nÎN, (n>N)Þ(|(x_n+y_n)-(a+b)|<e)

6° Если последовательности {x_n} и {y_n} сходятся к a и b, то последовательность {x_n-y_n} тоже сходиться, причем к (a-b).

Доказательство:

7° Если последовательности {x_n} и {y_n} сходятся к a и b, то последовательность {x_n*y_n}, тоже сходится, причем к (a*b).

Доказательство:

Зафиксируем e>0;

Рассмотрим 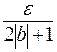>0, Для него найдем:

$N₁ÎN: "nÎN, (n>N)Þ(|x_n-a|< )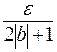

{x_n} – сходится, следовательно {x_n} ограничено:

Дата добавления: 2015-07-25