Уравнения идеальных газов

Уравнение состояния идеального газа в зависимости от его количества может иметь вид:

— для 1 кг газа; (1.1)

— для m кг газа; (1.2)

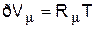— для 1 кмоля газа, (1.3)

где р – абсолютное давление, Па;

v – удельный объем газа, м³/кг;

V – объем данной массы газа, м³;

V_ – объем киломоля газа, м³/кмоль;

Т – абсолютная температура, К;

m – масса газа, кг;

 – масса киломоля газа, кг/кмоль;

R_ = 8314 Дж/(кмольЧК) – универсальная газовая постоянная;

– газовая постоянная, Дж/(кгЧК).

Согласно молекулярно–кинетической теории идеальных газов их удельные мольные и массовые изохорные и изобарные теплоемкости постоянны и рассчитываются по формулам

, кДж/(кмоль×К); (1.4)

, кДж/(кмоль×К); (1.5)

; (1.6)

, (1.7)

где i – число степеней свободы данного газа.

Для одноатомных газов i = 3; для двухатомных газов i = 5; для трех- и многоатомных газов i = 6. Для смеси идеальных газов i не имеет смысла и формулы (1.4) – (1.7) использовать нельзя.

Разность изобарной и изохорной теплоемкостей идеальных газов определяется соотношением Майера:

; . (1.8)

В расчетах политропных процессов используется коэффициент Пуассона, который для однородного газа определяется соотношением

. (1.9)

Для смеси идеальных газов i не имеет смысла, и ее в формуле (1.9) применительно к смесям газов использовать нельзя

Дата добавления: 2015-07-25