
|
Читайте также: |
Для устойчивой системы необходимо и достаточно, чтобы при изменение угловой частоты ω от 0 до 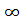 годограф, описываемый концом вектора G(jω) на плоскости комплексного переменного, начинался на вещественной положительной полуоси и, вращаясь только против часовой стрелки, нигде не обращаясь в нуль, проходил последовательно число квадрантов, которое равно степени n характеристического уравнения, повернувшись на угол
годограф, описываемый концом вектора G(jω) на плоскости комплексного переменного, начинался на вещественной положительной полуоси и, вращаясь только против часовой стрелки, нигде не обращаясь в нуль, проходил последовательно число квадрантов, которое равно степени n характеристического уравнения, повернувшись на угол 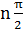 .
.
Для рассматриваемой замкнутой автоматической системы имеем характеристическое уравнение:

Подставляя вместо оператора р значение (jω) и отделяя вещественную часть от мнимой, получим:


где 
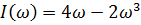
Находим координаты точек годографа Михайлова.
При  получим:
получим:
 ;
; 
При  получим:
получим:
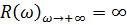 ;
; 
Положив  , находим значение ω, при которых годограф пересекает ось абсцисс:
, находим значение ω, при которых годограф пересекает ось абсцисс:




\
Приравняв 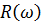 , к нулю, находим корни уравнения:
, к нулю, находим корни уравнения:
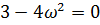


Сведем полученные данные в таблицу 2:
Таблица 2
| ω | R(ω) | I(ω) |
| 1,4 | -4,8 | |

| 1,1 |
Годограф имеет характер, показанный на рис.3;

Рис. 3. Годограф Михайлова.
Вывод: Годограф Михайлова пересекает последовательно оси координат, следовательно, автоматическая система устойчива.
Дата добавления: 2015-07-25; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Критерий Найквиста. | | | Опис конструкції і принцип дії системи автоматичного регулювання. |