Критерий Найквиста.

Система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если амплитудно-фазовая частотная характеристика W(jω) этой системы в разомкнутом состоянии не охватывает точку с координатами (-1; j0).

Находим комплексный коэффициент передачи для разомкнутой системы, подставляя jω вместо оператора p:

Так как j= 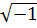; то , тогда:

Чтобы представить комплексный коэффициент передачи в виде комплексного числа, имеющего действительную R(ω) и мнимую I(ω) части, умножим и разделим полученный результат на сопряженное знаменателю комплексное число: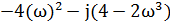

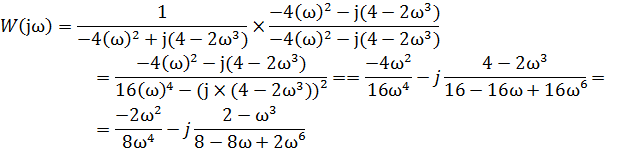
Давая различные значения частоте w, находим координаты R(ɷ) и I(ɷ) точек годографа комплексного коэффициента передачи. Лучше начинать нахождение координат точек годографа с характерных точек, а именно: с точки при ω→0, при ω→∞, точек, в которых годограф пересекает оси координат, а затем найти координаты промежуточных точек годографа.

При получим:

;

Найдем координаты точек, которые являются местом пересечения точек годографа с осью абсцисс. Т.е. должно соблюдаться условие:

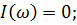
То есть, если числитель равен нулю:

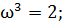
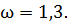
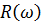Подставляя найденное значение в выражение для найдем координаты искомой точки на оси абсцисс:

По такому же методу найдем координаты точек пересечения годографа с осью ординат, т.е. :

;

.

При 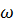→∞ получим, разделив числитель и знаменатель на ω²:

Сведем полученные данные в таблицу 1:

Таблица 1

ω	R(ω)	I(ω)
		0,25
1,3	0,15

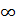
Годограф комплексного коэффициента передачи будет иметь вид, показанный на рис. 2.

Рис. 2. Годограф Найквиста

Вывод: замкнутая автоматическая система находится на границу устойчивости, так как амплитудно-фазовая характеристика разомкнутой системы проходит через точку с координатами (-1; j0).

Дата добавления: 2015-07-25