Исходные данные. Таблица-1Исходные данные № вар. Хим. СИМВОЛ Ширина запрещ

Таблица-1Исходные данные

№ вар.	Хим. СИМВОЛ	Ширина запрещ. Зоны Eg в эВ при 0К 300 к	mр /m0	* mn /mо	Температуры, К
	InP	1.42 1.35	0.64	0,077
Si	1,21	1,12	0,16

Теория

Собственный полупроводник – это беспримесный и бездефектный полупроводник. В собственных полупроводниках носители заряда образуются за счет теплового возбуждения электронов валентной зоны.

Рассчитаем концентрацию электронов проводимости:

(1)

где Nc – эффективная плотность состояний в зоне проводимости, она зависит от форма зоны - Е(p) и температуры (слабо).

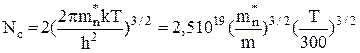, (2)

где m_n^* - эффективная масса электронов в зоне проводимости, m – масса о электрона, k- постоянная Больцмана, h- постоянная Планка [1].

Для того, чтобы рассчитать количество дырок в зоне проводимости учтем, что вероятность заполнения энергетического уровня дыркой равна:

(3)

Рассчитаем концентрацию дырок в валентной зоне:

(4)

где N_v – эффективная плотность состояний в валентной зоне.

(5)

Рассчитаем концентрацию электронов и дырок в собственном полупроводнике. Для этого мы должны определить для него положение уровня Ферми. Положение уровня Ферми в полупроводниках определяется из условия электронейтральности.

(6)

Откуда получим:

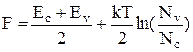(7)

Поскольку (E_c+E_v)/2 >>(kT/2)ln(N_v/N_c), то мы получили, что в собственном полупроводнике уровень Ферми лежит примерно посередине запрещенной зоны и его положение слабо зависит от температуры.

Обозначим концентрацию носителей в собственном полупроводнике через n_i² и рассчитаем чему равно произведение концентрации электронов и дырок, а так же значение n_i²:

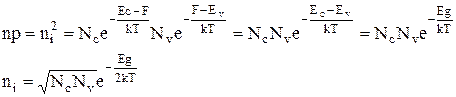(8)

Т.е. концентрация электронов и дырок растет с температурой по экспоненциальному закону с показателем равным половине ширины запрещенной зоны. Эту зависимость удобно представлять на графиках откладывая по вертикальной оси концентрацию в логарифмическом масштабе, а по горизонтальной обратную температуру 1/T (обычно откладывают 1000/T). Действительно прологарифмировав первое выражение получим:

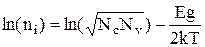(9)

5. Расчёт для кремния

6. Результаты расчётов

Таблица-2 Результаты расчета

	Eg эВ	T1 К	1000/T1	ln ni	Eg эВ	T2	1000/T2	ln ni
Si	1,21	300,00			1,21	400,00
InP	1,42	300,00			1,42	400,00

	Eg эВ	T3 К	1000/T3	ln ni	Eg эВ	T4	1000/T4	ln ni
Si	1,21	200,00			1,21	600,00
InP	1,42	200,00			1,42	600,00

Вывод

1.Собственная концентрация для InP значительно зависит от температуры чем для Si, что видно из графика.

2.Подвижность формально можно ввести как некоторый коэффициент пропорциональности между средней скоростью дрейфа носителей заряда в электрическом поле и величиной электрического поля. Подвижность слабо зависит от температуры. V=μE. Как следует из формулы, μE имеет размерность [см2/(В*с)]. Подвижность тем выше, чем реже электроны или дырки сталкиваются с атомами решетки, примесей или дефектами.

3.Концентрация носителей заряда в собственных полупроводниках возрастает с ростом температуры по экспоненциальному закону, при прочих равных условиях она больше в полупроводниках с малыми 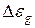.В области высокой температуры ширина запрещенной зоны полупроводника уменьшается по линейному закону:

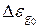- ширина запрещенной зоны при T = 0 K⁰.

Для нелегированных полупроводников она падает с увеличением температуры пропорционально T-3/2. Поэтому электропроводность для нелегированных материалов определяется изменением концентрации, которая экспоненциально растет с температурой.

Дата добавления: 2015-07-25