
|
Читайте также: |
Некоторые пределы
 (׀q ׀<1)
(׀q ׀<1)
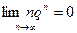 (׀q ׀<1)
(׀q ׀<1)
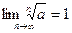 (a >0)
(a >0)

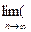 1+1/n)n = e
1+1/n)n = e 
 = 1
= 1
Эквивалентности при х →0
sin x ~ x tg x ~ x
arcsin x ~ x arctg x ~ x
1 – cos x ~ x2/2 ln (1+x) ~x
ax – 1 ~x ln a ex – 1 ~x
(1 + x)a – 1 ~ax
Некоторые пределы
 (׀q ׀<1)
(׀q ׀<1)
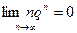 (׀q ׀<1)
(׀q ׀<1)
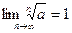 (a >0)
(a >0)

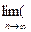 1+1/n)n = e
1+1/n)n = e 
 = 1
= 1
Эквивалентности при х →0
sin x ~ x tg x ~ x
arcsin x ~ x arctg x ~ x
1 – cos x ~ x2/2 ln (1+x) ~x
ax – 1 ~x ln a ex – 1 ~x
(1 + x)a – 1 ~ax
Некоторые пределы
 (׀q ׀<1)
(׀q ׀<1)
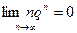 (׀q ׀<1)
(׀q ׀<1)
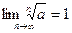 (a >0)
(a >0)

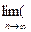 1+1/n)n = e
1+1/n)n = e 
 = 1
= 1
Эквивалентности при х →0
sin x ~ x tg x ~ x
arcsin x ~ x arctg x ~ x
1 – cos x ~ x2/2 ln (1+x) ~x
ax – 1 ~x ln a ex – 1 ~x
(1 + x)a – 1 ~ax
Дата добавления: 2015-07-25; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| РЕГУЛЯЦИЯ ФУНКЦИИ КЛЕТКИ | | | Некоторые пределы |