Исследование структуры систем автоматического регулирования.

Задание:

1) По заданным дифференциальным уравнениям элементов входящих в структуру определить их передаточные функции W(p).

2) Построить структурную схему САР и определить и её общую передаточную функцию при заданном входном воздействии по каналу регулирования.

3) Определить устойчивость САР по критерию Михайлова и критерию Гурвица. При неустойчивой работе структуры произвести коррекцию, определив изменённые коэффициенты и довести систему до устойчивого состояния.

Исходные данные (вариант №2, блок №4):

Дифференциальные уравнения:

1.

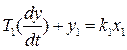
2.

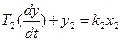
3.

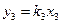
4.

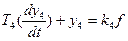
Уравнения связи элементов структурной схемы САУ:

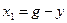
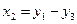
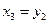
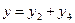
Коэффициенты дифференциальных уравнений приведены в таблице 1:

k1	T1	k2	T2	k3	k4	T4
			0,05	0,3	0,9	0,7

Решение:

1. Определение передаточных функций по заданным дифференциальным уравнениям.

a) T₁(p)+y₁(p)+y₁(p)=k₁x₁(p) y₁(p)*(T₁p+1)= k₁x₁(p)

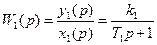
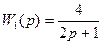
b) T₂(p)+y₂(p)+y₂(p)=k₂x₂(p) y₂(p)*(T₂p+1)= k₂x₂(p)

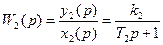
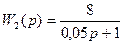
c) y₃=k₃x₃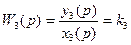

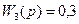
d) T₄(p)+y₄(p)+y₄(p)=k₄f₄(p) y₄(p)*(T₄p+1)= k₄f₄(p)

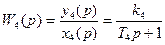
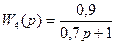
2. Структурная схема САУ. Передаточные функции замкнутой САУ по каналам управляющего и возмущающего воздействий.

W₄(p)

f

x₄

W₁(p)

W₂(p)

g x₁ y₁ x₂ y₂

y₃ x₃

W₃(p)

Определение передаточной функции замкнутой САУ.

Упростим схему объединив W2(p) и W3(p)

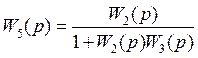
Определим передаточную функцию замкнутой системы W(p)зам.сис при f(p)=0.

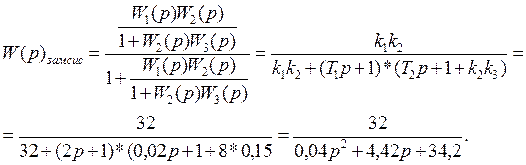
Определим передаточную функцию замкнутой системы по каналу возмущающего воздействия W(p)f при g(p)=0.

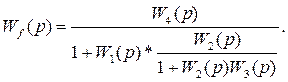
Полученную функцию исследуем на устойчивость замкнутой САУ по критериям устойчивости Гурьвица и Михайлова.

3. Исследование на устойчивость замкнутой САУ по критериям устойчивости Гурьвица и Михайлова.

Определение устойчивости САУ по критерию Гурьвица

Возьмем характеристическое уравнение:

D(p)=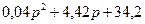

Если характеристическое уравнение имеет первый или второй порядок, то для устойчивости достаточно, что бы коэффициенты a0, a1, a2, были больше нуля.

Как видно из нашего характеристического уравнения коэффициенты a0>0 a1>0 a2>0, что является условие устойчивости САУ по критерию Гурьвица.

Определение устойчивости САУ по критерию Михайлова.

Возьмем наше характеристическое уравнение:

D(p)=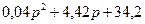

Подставив в уравнение p=jω и получим:

D(jω)=0,04 (jω)²+4,42 jω+34,2= -0,04ω²+4,42 jω+34,2

Выделим в данном уравнении вещественную и мнимую части:

Re(w)=34,2-0,04w²

Im(w)=4,42w

Зависимость от частоты реальной и мнимой частей характеристического уравнения представлена в таблице 2 и на рис. 2.

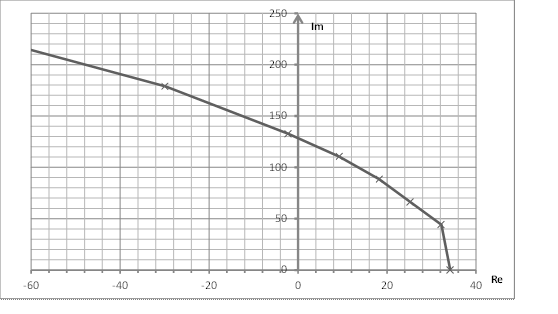
Рис.2

Таблица 2.

w
Re	34,2	30,2	25,2	18,2	9,2	-2,2	-29,8	-65,8
Im		44,2	66,3	88,4	110,5	132,6	176,8

Из рис. 2 видно, что годограф обходит начало координат в следующем порядке: 1ый квадрант, 2ой квадрант и уходит в ∞. Это является условием устойчивости САУ по критерию Михайлова.

4. Определение области устойчивости САУ методом D-разбиения

Определим область устойчивости САУ методом D-разбиения по коэффициенту усиления K1. Возьмем передаточную функцию замкнутой системы W(p) раз.сис

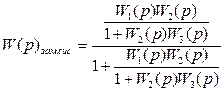
Подставим значения передаточных функций в передаточную функцию замкнутой системы W(p) раз.сис, получим:

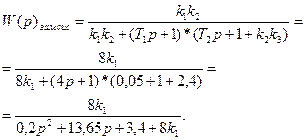
Из полученного выражения возьмем характеристическое уравнение замкнутой системы автоматического управления:

D(p)=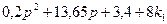

Запишем характеристическое уравнение в виде:

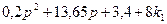=0

Построим облость устойчивости K₁ для системы:

· Выведем интересующий нас параметр.

k₁=-0,025p²-1,7p-0,43

Заменим p=jω, получим:

k₁=0,025 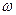²-1,7j 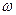-0,43

Выделим в данном уравнении вещественную и мнимую части:

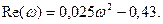
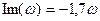
Зависимость от частоты реальной и мнимой частей характеристического уравнения представлена в таблице 3 и на рис. 3.

Таблица 3

ω					4,1					+∞
Re	-0,43	-0,41	-0,33	-0,21		0,2	1,17	2,07	9,6	+∞
Im		-1,7	-3,4	-5,1	-6,97	-8,5	-13,6	-17	-34	+∞

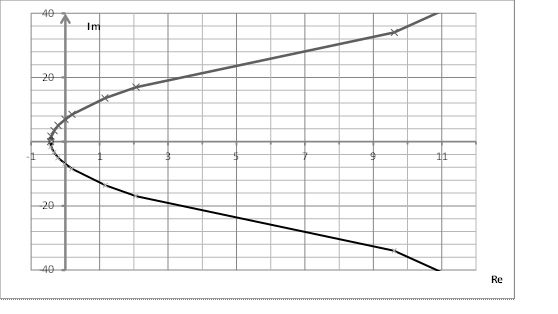
Рис.3

Осуществим проверку с помощью критерия Гурвица, для этого в характеристическое уравнение подставим значения К₁ не устойчивости, получим:

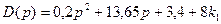
Подставим значение из области устойчивости k₁= 1.

Получим:

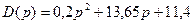
Видно что коэффициенты 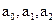, больше нуля, значит система устойчива.

Подставим значение из области не устойчивости k₁=-1, получим:

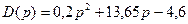
Видно что коэффициент a₂ меньше нуля, значит система не устойчива.

Проверка показала, область устойчивости была верно определена методом D-разбиения.

5. Расчет переходного процесса регулируемого параметра в САУ.

На рис. 4 представлена структурная схема САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

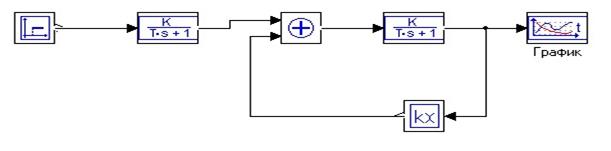
рис. 4 структурная схема САУ в программе МВТУ для расчета переходного прочеса по каналу управляющего воздействия.

На рис. 5 представлена кривая в программе МВТУ переходного процесса.

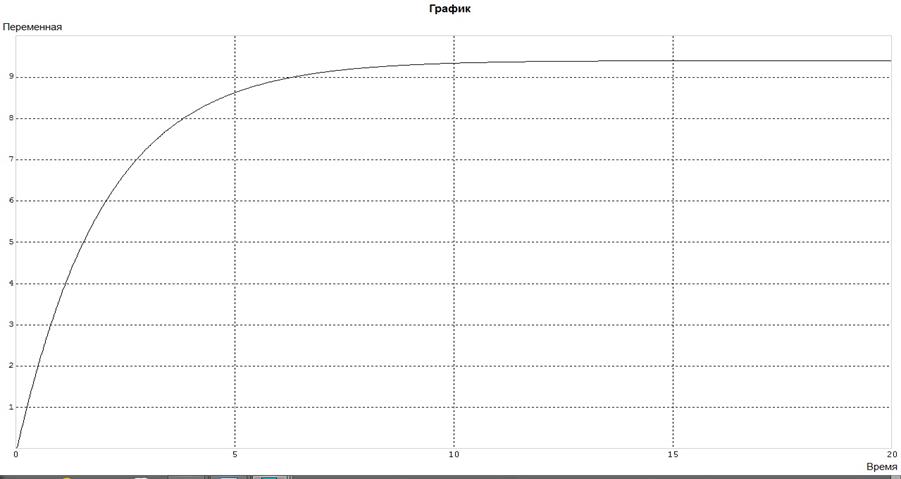
рис. 5 кривая в программе МВТУ переходного процесса.

6. Определение показателей качества регулирования и максимального регулируемого параметра.

По кривой представленной на рис. 5 определим время регулирования.

Для этого на кривой отмечаем 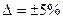от 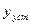, и проводим линии параллельные оси абцис. На пересечении кривой и нижней линии получаем точку это и есть время регулирования 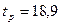. На рис. 6 представлена часть кривой переходного процесса.

По кривой представленной на рис.6 определяем максимальное ускорение .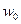

Для этого проводим касательные к точкам 0 и 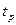и строим треугольники. Скорости находятся как отношений приращений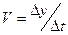

Получив скорости 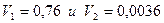подставляем в формулу для максимального ускорения :

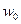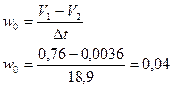
7. Определение показателей качества регулирования.

Показатели качества регулирования вычисляются по следующим формулам: 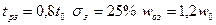. Получим:

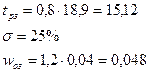
8. Построение ЛАЧХ 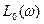не изменяемой части разомкнутой САУ.

Возьмем передаточную функцию разомкнутой САУ

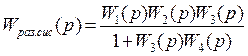
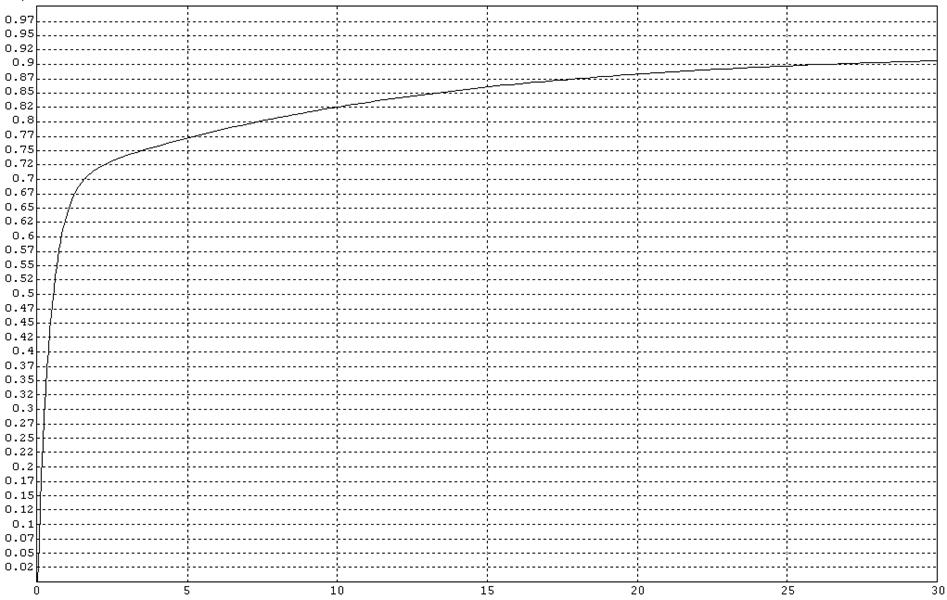
рис. 6 часть кривой переходного процесса

Подставив значения передаточных функций получим:

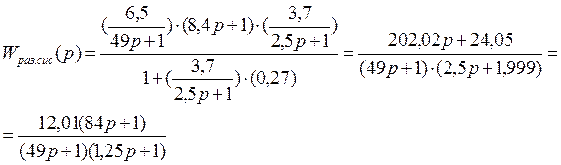
Найдем сопряженные частоты:

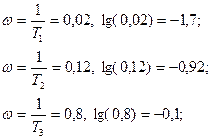
На рис.7 представлена ЛАЧХ 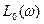не изменяемой части разомкнутой САУ.

9. Построение желаемой ЛАЧХ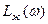

Для построения желаемой ЛАЧХ 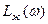, найдем частоту среза 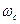, для среднечастотной асимптоты. Для этого используем номограмму, составленная В.В. Солодниковым на рис. 8. По заданному значению перерегулирования 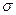определим отношение между 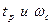. Используя формулу:

.

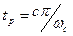Дано 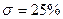, от сюда получаем 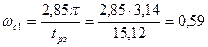, тем самым мы нашли частоту при которой время регулирования не превысит заданного значения. При начальном рассогласовании ускорение регулируемой величины ограничивается значением 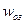, то максимальное значение определяется из отношения:

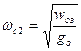, где 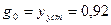. Получим:

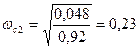
Т.к. 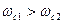, то частоту среза принимаем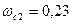

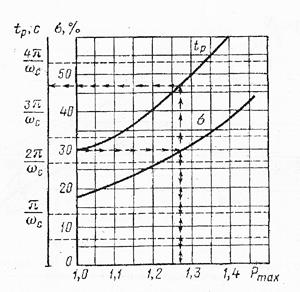
Рис.8 Показатели качества регулирования САУ в зависимости от максимума вещественной частотной характеристики разомкнутой системы.

Среднечастотная асимптота желаемой ЛАЧХ проводится через частоту среза с наклоном -20 дБ/дек.

Найдем частоту сопряжения с низкочастотной областью. Для этого воспользуемся номограммой на рис. 9, по ней определяем предельные значения логарифмических амплитуд. В нашем случае это значение 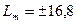. На этих отметках проводим линии параллельные оси частот. В точках пересечения этих линий и средне частотной асимптоты мы получаем сопрягающие частоты. Для определения низкочастотной области воспользуемся следующим выражением .

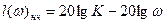Возьмем ω= 1 получим: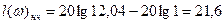

Возьмем ω=К получим: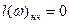

По этим 2 тучкам строем наклонную линию АВ, её наклон -20дБ/дек.

Из точки сопряжения низкочастотной и среднечастотной проводим наклонную, с наклоном -40дБ/дек, до пересечения с линией АВ.

Высокочастотную асимптоту проводим параллельно желаемой ЛАЧХ, т.к. она мало влияет на свойства системы.

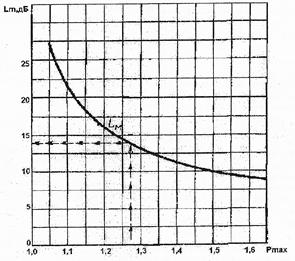
Рис. 9 Зависимость значений желаемой ЛАЧХ на границах среднего поддиапаозона от максимума вещественной частотной характеристики разомкнутой системы.

На рис.7 представлена желаемая ЛАЧХ .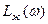

10. Определение ЛАЧХ 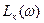корректирующего звена.

Т.к в нашей системе корректирующее звено последовательное, то для построения ЛАЧХ 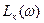корректирующего звена, воспользуемся формулой:

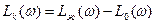
На рис.7 представлена ЛАЧХ 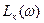корректирующего звена.

11. Определение передаточной функции 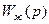разомкнутой САУ по желаемой ЛАЧХ .

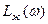Для определения передаточной функции 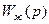разомкнутой САУ по желаемой ЛАЧХ 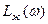воспользуемся рис.7. Получим:

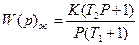
Найдем частоты сопряжения и получим Т

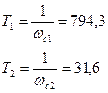
По ЛАЧХ 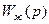показанной на рис.7 найдем К= 21,6

Подставим найденные Т, получим

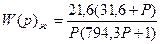
12. Определение передаточной функции 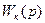корректирующего звена по ЛАЧХ .

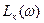Для определения передаточной функции 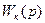разомкнутой САУ корректирующего звена по полученной ЛАЧХ 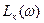воспользуемся рис.7. Получим:

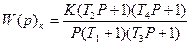
Найдем частоты сопряжения и получим Т

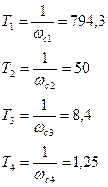
По ЛАЧХ 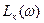показанной на рис.7 найдем К= 0,63.

Подставим найденные Т и К, получим

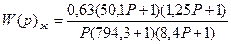
Дата добавления: 2015-07-25