Книга V. Нелинейность и нелинейность

Более строгим языком, сообразующимся с графиками, из Taleb and Douady (2012): локальная хрупкость случайной переменной X_λ, зависящей от параметра λ, на уровне стресса K и на уровне полуотклонения s ^– ( λ ) с функцией распределения вероятностей f _λ – это ее чувствительность к полувеге с K‑левым хвостом («вега» – это чувствительность к некоторой мере волатильности), V (X, f _λ, K, s ^– ) к s ^–, среднее абсолютное полуотклонение ниже Ω, здесь –

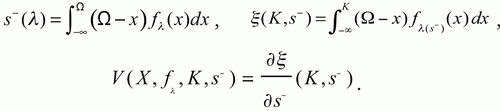
Унаследованная хрупкость Y в отношении к X на уровне стресса L φ (K) и уровень левого полуотклонения s ^– ( λ ) от X – это частная производная

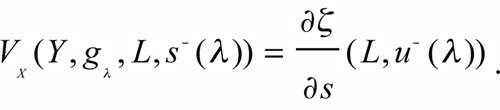
Уровень стресса и функция распределения вероятностей определены для переменной Y, однако параметр, использованный для дифференцирования, – это левое полуабсолютное отклонение X. Для антихрупкости: скачок выше Ω в дополнение к неуязвимости под тем же самым уровнем стресса K. Теоремы переноса связывают хрупкость Y со второй производной φ (K) и показывают эффект выпуклых (вогнутых или смешанных нелинейных) преобразований на хвостах посредством функции переноса H ^K . Для антихрупкости используйте s ⁺ , интеграл в промежутке от K до плюс бесконечности.

Хрупкость не связана с психологией. Мы начали с определения хрупкости как чувствительности к хвостовой веге и заканчиваем нелинейностью как необходимым свойством источника подобной хрупкости в унаследованном случае; это скорее причина болезни, чем сама болезнь. Однако экономисты и специалисты по принятию решений много лет пишут о том, что риск связан с психологическими предпочтениями. Исторически риск описывался как производная от антипатии к риску, то есть как результат структуры опций в условиях неопределенности с вогнутостью путаной концепции «полезности» отдачи; см. Pratt (1964), Arrow (1965), Rothschild and Stiglitz (1970, 1971). Однако эти разговоры о «полезности» не привели нас ни к чему, кроме хождения по кругу, на что указали Machina and Rothschild (2008): «Риск – это то, чего не любят те, кто не любит риск». Сводить риск к антипатии к вогнутым опциям – это печальный результат.

Фарфоровая чашка и ее вогнутость. В самом деле, у кофейной чашки, дома или моста нет психологических предпочтений, субъективной полезности и прочего. Однако все эти вещи вогнуты в отношении реакции на вред: если мы примем, что z – уровень стресса, а Π (z) – функция вреда, достаточно показать, что при n>1 Π (n z) < n Π (z) для всех 0< n z<Z*, где Z* – уровень (не обязательно известный), на котором вещь разрушается. Из неравенства следует, что у Π (z) есть отрицательная вторая производная в точке исходной величины z. И если кофейной чашке меньше вредит воздействующий на нее n раз стрессор интенсивности Z, чем воздействующий на нее один раз стрессор n Z, значит, вред (как негативная функция) должен быть вогнутым в отношении стрессоров вплоть до точки разрушения; подобное ограничение налагается структурой вероятностей выживания и распределением вредных событий – и не имеет ничего общего с субъективной полезностью или другими выдумками.

Позитивный эффект масштаба, выпуклость городов. Bettencourt and West (2010, 2011), West (2011). Города – трехмерные организмы, похожие на животных, и позитивная нелинейность в них соответствует эффективности. Если б не эти ужасные пробки!

«Больше – значит по‑разному». Anderson (1972).

Сравнительная хрупкость животных. Diamond (1988).

Фливберг и коллеги по опозданиям. Flyvbjerg (2009), Flyvbjerg and Buzier (2011).

Маленькое красиво, романтический взгляд. Dahl and Tufte (1973), Schumacher (1973) – для звучных цитат. Kohr (1957) – в качестве первого манифеста против размера властных структур.

Размер правительства. Я не смог найти тех, кто рассуждает об этой проблеме в терминах выпуклости, даже среди либертарианцев. Пусть будет Kahn (2011).

Маленькие государства живут лучше. Древняя традиция изучения городов‑государств и управления ими. Кажется, наше восприятие политической системы зависит от размера. Свидетельства см. в Easterly and Kraay (2000).

Эпоха увеличения хрупкости. Zajdenwebber, см. обсуждение в «Черном лебеде». Уточненные цифры см. в The Economist, Counting the Cost of Calamities, 14.01.2012.

Эффект выпуклости на среднюю величину. Jensen (1906), Van Zwet (1966). Йенсен рассматривает монотонные функции, ван Цвет – вогнуто‑выпуклые и прочие, но не выходит за пределы простой нелинейности. Taleb and Douady (2012) применили рассуждение ко всякой локальной нелинейности.

Эмпирические свойства укрупнения. Слияния и гипотеза высокомерия: Roll (1986); из недавних работ – Cartwright and Schoenberg (2006).

Долг в древней истории. Вавилонские праздники: Hudson et al. (2002). Афины: Harrison (1998), Finley (1953). История долга: Barty‑King (1997), Muldrew (1993), Glaeser (2001). Последний рассматривает ее с точки зрения анархизма. Он на самом деле считает, что долг возник прежде бартерного обмена.

Пищевые цепочки. Dunne et al. (2002), Perchey and Dunne (2012), Valdovinos and Ramos‑Jiliberto (2010). Хрупкость и ресурсы: Nasr (2008, 2009).

Fannie Mae. Компания была вогнутой в отношении любых значимых переменных. Какой‑то обиженный непониманием вероятности и нелинейности парень из комиссии Обамы, изучавшей причины кризиса, пустил слух, будто бы я всего лишь распознал риск Fannie Mae в отношении процентной ставки. Неправда.

Издержки исполнения. «Издержки ценового влияния», они же издержки исполнения, растут вместе с масштабом; они выражаются формулой с квадратным корнем – что означает, что суммарная цена выпукла и растет по формуле с показателем степени 3/2 (что означает, что расходы вогнуты). Но беда в том, что для больших отклонений, таких, как в случае с Société Générale, все куда хуже; операционные издержки растут с ускорением, и предсказать их точно невозможно – все статьи о «ценовом влиянии» по новой научной традиции бессмысленны ровно там, где они должны быть внятны. Что характерно, Бент Фливберг обнаружил, что схожий эффект, пусть и немного менее вогнутый в конечном итоге, наблюдается при строительстве мостов и туннелей – пропорциональные издержки растут с масштабом как 10 Log [x].

Маленькое красиво, математический подход. Объясним, почему города‑государства, маленькие фирмы и т. д. куда менее уязвимы в отношении опасных событий. Пусть X, случайная переменная, обозначающая «непредусмотренный риск», – источник неопределенности (фирма Société Générale этого источника в упор не видела; для корпорации таким источником может быть острая нужда в переучете и т. д.). Предположим, что размер непредусмотренного вреда пропорционален размеру объекта, потому что у малых объектов транзакции меньше, у крупных больше. В качестве распределения вероятностей используем переменную суммарного непредусмотренного риска Σ X _i, где X _{i –} независимые случайные переменные, определяемые просто как X _i = X/N. При хвостовой амплитуде k и хвостовой экспоненте α имеем: π (k, α, X) = α k ^α x ^{–1 – α}. N ‑свернутое распределение Парето для непредусмотренной суммы риска: N Σ X _i: π (k/N, α, X) _N, где N – это число сверток распределения. Среднее значение распределения, инвариантное по отношению к N, – это α k/ α –1).

Потери от вынужденных перерасходов. Пусть для функции потерь C[X] = – b X ^β, где издержки вреда – вогнутая функция от X. Для небольших отклонений β = 3/2 в литературе о микроструктуре и исполнении.

Итоговое распределение вероятностей вреда. Поскольку нас интересует распределение y, преобразуем стохастическую переменную. Для вреда y=C [X] имеем распределение π [C ^‑1 [x]] /C’ [C ^‑1 [x]]. Это распределение по Парето с хвостовой амплитудой k^β и хвостовой экспонентой α/β,

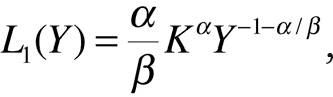
со средним значением

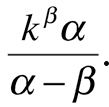
Теперь сумма: для суммы свертки для N объектов асимптотическое распределение имеет вид

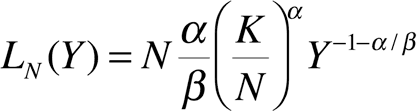
со средним значением (ввиду суммируемости) в виде функции от переменных, включая N:

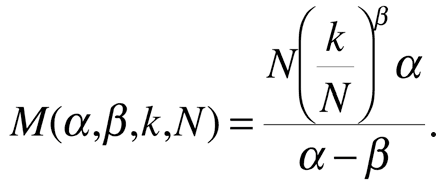
Если теперь мы посмотрим на соотношение ожидаемых потерь в хвостах от N=1 до N=10 при различных значениях отношения β к α, соотношение ожидания для одного объекта к ожиданию для 10 объектов

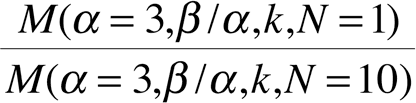
даст эффект «маленькое красиво» при разных уровнях вогнутости.

Дата добавления: 2015-07-20