
Читайте также:
|
В задачах считается, что система координат прямоугольная декартова.
1. Составьте каноническое уравнение эллипса, если:
1) его полуоси равны  и
и 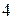 ;
; 
2) расстояние между фокусами равно 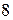 и большая полуось равна
и большая полуось равна  ;
;
3) большая полуось равна  и эксцентриситет
и эксцентриситет 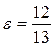 ;
;
4) расстояния от одного из фокусов до концов большей оси соответственно равны  и
и  ;
;
5) прямые 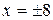 являются директрисами, а малая ось равна
являются директрисами, а малая ось равна 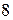 ;
;
6) расстояние между вершинами, лежащими на большей оси, равно 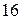 , а расстояние между фокусами равно
, а расстояние между фокусами равно  ;
;
7) фокусами эллипса являются точки  , а точка
, а точка  принадлежит эллипсу;
принадлежит эллипсу;
8) фокусами эллипса являются точки  , а директрисами являются прямые
, а директрисами являются прямые  ;
;
9) расстояние от директрисы до ближайшей вершины равно 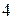 , а до вершины, лежащей на оси, параллельной директрисе, равно
, а до вершины, лежащей на оси, параллельной директрисе, равно 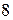 ;
;
10) треугольник с вершинами в фокусах и в конце малой оси правильный, а диаметр окружности, проходящей через центр и две вершины эллипса, равен  .
.
2. Составьте уравнение семейства эллипсов, имеющих одни и те же фокусы, 

3. Оси эллипса совпадают с осями координат. Составьте уравнение эллипса, если известно, что эллипс проходит через точки 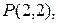

4. Определите эксцентриситет эллипса, зная, что:
1) его малая ось видна из фокуса под прямым углом;
2) расстояние между фокусами равно расстоянию между вершинами малой и большой осей;
3) расстояние между директрисами в четыре раза больше расстояния между фокусами;
4) отрезок между фокусом и дальней вершиной большей оси делится вторым фокусом в отношении 2:1.
5. Известно, что фокус эллипса имеет координаты ( ), ему соответствует директриса
), ему соответствует директриса 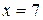 , а эксцентриситет
, а эксцентриситет  равен 1/2. Найдите второй фокус и вторую директрису этого эллипса.
равен 1/2. Найдите второй фокус и вторую директрису этого эллипса.
6. Определите эксцентриситет эллипса, если расстояние между фокусами есть среднее арифметическое длин его осей.
7. Через фокус эллипса  проведена хорда, перпендикулярная к большей оси. Найдите длину этой хорды.
проведена хорда, перпендикулярная к большей оси. Найдите длину этой хорды.
8. Найдите эксцентриситет эллипса, зная, что стороны вписанного в него квадрата проходят через фокусы эллипса параллельно его малой оси.
9. Составьте уравнение прямой, проходящей через середины хорд эллипса  , лежащих на прямых
, лежащих на прямых  и
и 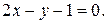
10. Через точку  большей оси эллипса
большей оси эллипса  проведена хорда с угловым коэффициентом
проведена хорда с угловым коэффициентом  . Найдите длину этой хорды.
. Найдите длину этой хорды.
11. Докажите, что среди хорд эллипса, параллельных заданной прямой, максимальную длину имеет хорда, проведенная через центр эллипса. Такая хорда называется диаметром эллипса.
12. Докажите, что две параллельные хорды эллипса равны тогда и только тогда, когда они симметричны относительно центра эллипса.
13. Многоугольник называется вписанным в эллипс, если все его вершины принадлежат этому эллипсу. Докажите, что диагонали параллелограмма, вписанного в эллипс, являются его диаметрами.
14. Докажите, что стороны прямоугольника, вписанного в эллипс, параллельны его осям.
15. Дан эллипс  . Вычислите длину стороны квадрата, вписанного в этот эллипс.
. Вычислите длину стороны квадрата, вписанного в этот эллипс.
16. Докажите, что максимальная площадь параллелограмма, вписанного в эллипс  , две стороны которого параллельны заданной прямой, равна
, две стороны которого параллельны заданной прямой, равна  .
.
17. Докажите, что стороны прямоугольника максимальной площади, вписанного в эллипс  , равны
, равны 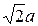 и
и 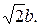
18. Докажите, что геометрическое место середин хорд эллипса  с угловым коэффициентом k есть диаметр эллипса с угловым коэффициентом
с угловым коэффициентом k есть диаметр эллипса с угловым коэффициентом 
19. Докажите, что сторона ромба, вписанного в эллипс  пересекает большую ось эллипса в точке с абсциссой
пересекает большую ось эллипса в точке с абсциссой  , где
, где  – угловой коэффициент этой стороны.
– угловой коэффициент этой стороны.
20. Докажите, что если 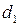 и
и 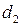 – длины взаимно перпендикулярных диаметров эллипса, то величина
– длины взаимно перпендикулярных диаметров эллипса, то величина  постоянна.
постоянна.
21. Напишите уравнения эллипса и гиперболы с фокусами  и
и 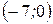 , проходящих через точку
, проходящих через точку  .
.
22. Составьте каноническое уравнение гиперболы, если:
1) действительная и мнимая полуоси соответственно равны  и
и  ;
;
5) фокальное расстояние равно  и вещественная полуось равна
и вещественная полуось равна 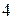 ;
;
6) вещественная полуось равна 24 и эксцентриситет  ;
;
7)действительная полуось равна 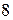 , а угол
, а угол  между асимптотой и действительной осью равен
между асимптотой и действительной осью равен 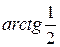 ;
;
8) расстояние между вершинами равно  , а расстояние между фокусами равно
, а расстояние между фокусами равно  ;
;
9) действительная полуось равна  , а точка
, а точка  принадлежит гиперболе;
принадлежит гиперболе;
10) угол между асимптотами, содержащий фокус, равен 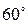 , а расстояние от директрисы до ближайшей вершины равно
, а расстояние от директрисы до ближайшей вершины равно 
11) эксцентриситет гиперболы равен 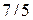 , а расстояние от вершины до ближайшего фокуса равно
, а расстояние от вершины до ближайшего фокуса равно  ;
;
12) точка  принадлежит гиперболе, а асимптотами являются прямые
принадлежит гиперболе, а асимптотами являются прямые 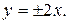
23. Известно, что фокус гиперболы имеет координаты 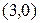 , ему соответствует директриса
, ему соответствует директриса  , а эксцентриситет е равен
, а эксцентриситет е равен 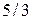 . Найдите второй фокус и вторую директрису этой гиперболы.
. Найдите второй фокус и вторую директрису этой гиперболы.
24. Пусть две гиперболы имеют общие асимптоты. Докажите, что:
1) если эти гиперболы лежат в одной и той же паре вертикальных углов, образованных их асимптотами, то их эксцентриситеты равны между собой;
2) если эти гиперболы лежат в разных парах вертикальных углов, образованных их асимптотами, то произведение их эксцентриситетов больше или равно  , причем это произведение равно
, причем это произведение равно  только для равносторонних гипербол.
только для равносторонних гипербол.
25. Напишите уравнение гиперболы, зная четыре точки 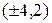 ,
,  пересечения ее директрис и асимптот.
пересечения ее директрис и асимптот.
26. Найдите эксцентриситет равносторонней гиперболы.
27. Дана равносторонняя гипербола 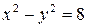 . Найдите гиперболу с теми же фокусами, проходящую через точку
. Найдите гиперболу с теми же фокусами, проходящую через точку 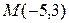 . На гиперболе
. На гиперболе 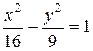 найдите точку, для которой фокальные радиусы взаимно перпендикулярны.
найдите точку, для которой фокальные радиусы взаимно перпендикулярны.
28. Докажите, что произведение расстояний от любой точки гиперболы до двух ее асимптот есть величина постоянная.
29. Составьте уравнение такой хорды гиперболы 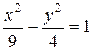 , которая точкой
, которая точкой 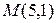 делится пополам.
делится пополам.
30. Докажите, что любая прямая пересекает гиперболу не более чем в двух точках.
31. Хордой гиперболы называется отрезок, концы которого лежат на гиперболе. Покажите, что хорды гиперболы лежат на прямых, не параллельных ее асимптотам.
32. Найдите длину хорды гиперболы 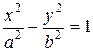 , если ее угловой коэффициент равен k (
, если ее угловой коэффициент равен k ( ) и она проходит через точку (
) и она проходит через точку ( ) действительной оси гиперболы.
) действительной оси гиперболы.
33. Докажите, что при 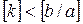 хорда гиперболы
хорда гиперболы 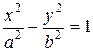 с угловым коэффициентом
с угловым коэффициентом  соединяет две различные ветви гиперболы. Покажите, что среди всех таких хорд наименьшую длину имеет хорда, проходящая через центр гиперболы. Эта хорда называется диаметром гиперболы.
соединяет две различные ветви гиперболы. Покажите, что среди всех таких хорд наименьшую длину имеет хорда, проходящая через центр гиперболы. Эта хорда называется диаметром гиперболы.
34. Докажите, что две параллельные хорды гиперболы равны тогда и только тогда, когда они симметричны относительно центра гиперболы.
35. Многоугольник называется вписанным в гиперболу, если все его вершины принадлежат этой гиперболе. Докажите, что диагонали параллелограмма, вписанного в гиперболу, являются его диаметрами.
36. Докажите, что стороны прямоугольника, вписанного в гиперболу, параллельны ее осям.
37. Дана гипербола 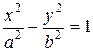 . Найдите вершины квадрата, вписанного в эту гиперболу, и указать, в каком случае такое построение возможно.
. Найдите вершины квадрата, вписанного в эту гиперболу, и указать, в каком случае такое построение возможно.
38. Стороны квадрата, вписанного в гиперболу, проходят через ее фокусы. Найдите ее эксцентриситет.
39. Составьте каноническое уравнение параболы, если:
1) расстояние от фокуса до вершины параболы равно  ;
;
2) расстояние от фокуса до директрисы равно  ;
;
3)длина хорды, проходящей через фокус параллельно директрисе, равна  ;
;
4)длина хорды, проходящей через фокус под углом  к оси параболы, равна
к оси параболы, равна  .
.
40. Найдите координаты фокуса и уравнение директрисы параболы 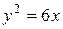 .
.
41. На параболе  найдите точку, фокальный радиус которой равен
найдите точку, фокальный радиус которой равен  .
.
42. На параболе  найдите точку
найдите точку  такую, что:
такую, что:
1) прямая, проходящая через точку М и фокус параболы, образует с осью  угол
угол 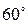 ;
;
2) площадь треугольника с вершинами в искомой точке  , фокусе параболы и точке пересечения оси параболы с директрисой равна
, фокусе параболы и точке пересечения оси параболы с директрисой равна  ;
;
3) расстояние от точки  до вершины параболы равно расстоянию от точки
до вершины параболы равно расстоянию от точки  до фокуса;
до фокуса;
4) расстояния от точки  до вершины параболы и до фокуса параболы относятся как
до вершины параболы и до фокуса параболы относятся как 
43. Через фокус параболы  проведена хорда, перпендикулярная к ее оси. Определите длину этой хорды.
проведена хорда, перпендикулярная к ее оси. Определите длину этой хорды.
44. Найдите такую хорду параболы  , которая точкой
, которая точкой 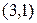 делится пополам.
делится пополам.
45. Найдите длину стороны равностороннего треугольника, вписанного в параболу 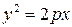 так, что одна из вершин треугольника совпадает с вершиной параболы.
так, что одна из вершин треугольника совпадает с вершиной параболы.
46. Напишите уравнение касательной к эллипсу  в точке
в точке 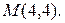
47. Составьте уравнения касательных к эллипсу 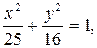 проходящих через точку
проходящих через точку 
48. Дана прямая 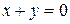 . Составьте уравнения касательных к эллипсу
. Составьте уравнения касательных к эллипсу  :
:
1) параллельных данной прямой;
2) перпендикулярных данной прямой.
49. Докажите, что произведение расстояний от фокусов эллипса до любой его касательной есть величина постоянная, равная квадрату малой полуоси.
50. Дан эллипс  и прямая
и прямая  . Найдите условия, необходимые и достаточные для того, чтобы данная прямая:
. Найдите условия, необходимые и достаточные для того, чтобы данная прямая:
1) пересекала эллипс в двух точках;
2) касалась эллипса;
3) не имела с эллипсом общих точек.
51. Эллипс, имеющий фокусы в точках 
 касается прямой
касается прямой 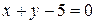 . Составьте уравнение эллипса.
. Составьте уравнение эллипса.
52. Найдите геометрическое место точек, из которых можно провести взаимно перпендикулярные касательные к эллипсу 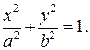
53. Точка  называется внутренней по отношению к эллипсу, если любая прямая, проходящая через
называется внутренней по отношению к эллипсу, если любая прямая, проходящая через  , пересекает эллипс в двух точках. Найдите условие, необходимое и достаточное для того, чтобы точка
, пересекает эллипс в двух точках. Найдите условие, необходимое и достаточное для того, чтобы точка 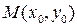 была внутренней для эллипса
была внутренней для эллипса 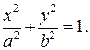
54. Докажите, что точка  будет внешней по отношению к эллипсу тогда и только тогда, когда из
будет внешней по отношению к эллипсу тогда и только тогда, когда из  можно провести к этому эллипсу две различные касательные.
можно провести к этому эллипсу две различные касательные.
55. Составьте уравнение касательной к гиперболе  в точке
в точке 
56. Составьте уравнение касательных к гиперболе  , проходящих через точку
, проходящих через точку 
57. Составьте уравнение касательной к гиперболе  , если касательная:
, если касательная:
1) параллельна прямой 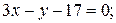
2) перпендикулярна к прямой 
58. Составьте уравнение гиперболы, зная уравнения ее асимптот  и уравнение одной из ее касательных
и уравнение одной из ее касательных 
59. Гипербола, оси которой совпадают с осями координат, касается прямой  в точке
в точке 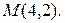 Составьте уравнение этой гиперболы.
Составьте уравнение этой гиперболы.
60. Даны гипербола 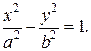 и прямая
и прямая  Найдите необходимые и достаточные условия для того, чтобы данная прямая:
Найдите необходимые и достаточные условия для того, чтобы данная прямая:
1) касалась гиперболы;
2) пересекала каждую ветвь гиперболы ровно в одной точке;
3) пересекала одну из ветвей гиперболы в двух точках;
4) пересекала ровно одну ветвь гиперболы в единственной точке.
61. Дана произвольная гипербола.
1) Существует ли общая касательная к обеим ветвям гиперболы?
2) Существует ли прямая, пересекающая каждую ветвь гиперболы в двух точках?
62. Можно ли к гиперболе  провести касательные с любым угловым коэффициентом
провести касательные с любым угловым коэффициентом  ? Если нет, то какому ограничению должен удовлетворять параметр
? Если нет, то какому ограничению должен удовлетворять параметр  ?
?
63. При каком условии из точки 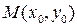 к гиперболе
к гиперболе  можно провести две касательные? Составьте уравнения этих касательных.
можно провести две касательные? Составьте уравнения этих касательных.
64. Определите произведение расстояний от фокусов гиперболы  до какой-либо ее касательной.
до какой-либо ее касательной.
65. Найдите площадь треугольника, образованного асимптотами гиперболы  и произвольной касательной к этой гиперболе.
и произвольной касательной к этой гиперболе.
66. Докажите, что точка гиперболы служит серединой отрезка касательной к этой гиперболе, заключенного между асимптотами.
67. Эллипс и гипербола имеют общие фокусы. Докажите, что они пересекаются под прямым углом, т.е. касательные, построенные в точке пересечения к этим эллипсу и гиперболе, взаимно перпендикулярны.
68. Найдите геометрическое место точек, из которых можно провести взаимно перпендикулярные касательные к гиперболе 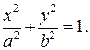
69. Точка  называется внутренней по отношению к гиперболе, если любая прямая, проходящая через
называется внутренней по отношению к гиперболе, если любая прямая, проходящая через  и не параллельная ни одной из асимптот, пересекает гиперболу в двух точках. Найдите условие, необходимое и достаточное для того, чтобы точка
и не параллельная ни одной из асимптот, пересекает гиперболу в двух точках. Найдите условие, необходимое и достаточное для того, чтобы точка  была внутренней для гиперболы
была внутренней для гиперболы  .
.
70. Докажите, что точка  , не совпадающая с центром гиперболы, будет внешней для этой гиперболы тогда и только тогда, когда из
, не совпадающая с центром гиперболы, будет внешней для этой гиперболы тогда и только тогда, когда из  можно провести к гиперболе по крайней мере одну касательную.
можно провести к гиперболе по крайней мере одну касательную.
71. Дано уравнение касательной 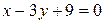 к параболе
к параболе 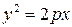 . Составьте уравнение параболы.
. Составьте уравнение параболы.
72. Дана парабола 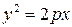 и прямая
и прямая  . Найдите условия, необходимые и достаточные для того, чтобы данная прямая:
. Найдите условия, необходимые и достаточные для того, чтобы данная прямая:
1) касалась параболы;
2) пересекала параболу в одной точке;
3) пересекала параболу в двух точках;
4) не имела с параболой общих точек.
73. Докажите, что если из любой точки, не лежащей на параболе, можно провести либо две, либо ни одной касательной к этой параболе.
74. Найдите геометрическое место середин отрезков касательных к параболе 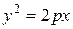 , заключенных между осями координат.
, заключенных между осями координат.
75. Найдите геометрическое место оснований перпендикуляров, опущенных из фокуса параболы  на ее касательные.
на ее касательные.
76. Найдите геометрическое место точек, из которых можно провести взаимно перпендикулярные касательные к параболе  .
.
77. Точка  называется внутренней по отношению к параболе, если любая прямая, проходящая через
называется внутренней по отношению к параболе, если любая прямая, проходящая через  и пересекающая ось параболы, имеет с этой параболой две общие точки. Найдите условие, необходимое и достаточное для того, чтобы точка
и пересекающая ось параболы, имеет с этой параболой две общие точки. Найдите условие, необходимое и достаточное для того, чтобы точка 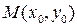 была внутренней для параболы.
была внутренней для параболы.
78. Докажите, что точка  будет внешней для параболы тогда и только тогда, когда из
будет внешней для параболы тогда и только тогда, когда из  можно провести к этой параболе две различные касательные.
можно провести к этой параболе две различные касательные.
79. Найдите геометрическое место точек, делящих в отношении  хорды окружности
хорды окружности 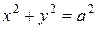 , параллельные оси
, параллельные оси  .
.
80. Отрезок постоянной длины скользит своими концами по двум взаимно перпендикулярным прямым. Точка М делит этот отрезок на два отрезка, длины которых равны 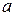 и
и 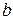 . Найдите линию, описываемую точкой М при движении отрезка.
. Найдите линию, описываемую точкой М при движении отрезка.
81. Даны точки  и
и  Найдите геометрическое место точек пересечения прямых, проходящих через точки
Найдите геометрическое место точек пересечения прямых, проходящих через точки 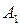 и
и  , отсекающих на оси ординат отрезки, произведение величин которых равно.
, отсекающих на оси ординат отрезки, произведение величин которых равно.
82. Около начала координат 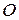 как центра описаны две окружности радиусами
как центра описаны две окружности радиусами 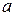 и
и 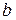 . Луч, вращающийся вокруг точки
. Луч, вращающийся вокруг точки 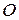 , пересекает эти окружности соответственно в точках
, пересекает эти окружности соответственно в точках  и
и  . Через точку
. Через точку  проводится прямая, параллельная оси абсцисс, а через точку
проводится прямая, параллельная оси абсцисс, а через точку  – прямая, параллельная оси ординат. Найдите геометрическое место точек
– прямая, параллельная оси ординат. Найдите геометрическое место точек  пересечения этих двух прямых при вращении луча.
пересечения этих двух прямых при вращении луча.
83. Найдите геометрическое место центров окружностей, касающихся двух данных окружностей, одна из которых расположена строго внутри другой.
84. Найдите геометрическое место центров окружностей, касающихся данной окружности и проходящих через данную точку, лежащую внутри этой окружности.
85. Даны точки  и
и  . Найдите геометрическое место точек пересечения прямых, проходящих через точки
. Найдите геометрическое место точек пересечения прямых, проходящих через точки 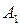 и
и  отсекающих на оси ординат отрезки, произведение величин которых равно
отсекающих на оси ординат отрезки, произведение величин которых равно  .
.
86. Найдите геометрическое место центров окружностей, касающихся внешним образом двух данных окружностей, одна из которых расположена вне другой.
87. Найдите геометрическое место точек, произведение расстояний от которых до двух противоположных сторон заданного прямоугольника равно произведению расстояний до двух других его противоположных сторон.
88. Найдите геометрическое место центров окружностей, касающихся данной окружности и проходящих через данную точку, лежащую вне этой окружности.
89. Найдите геометрическое место точек, для каждой из которых произведение расстояний до двух пересекающихся прямых равно заданному положительному числу.
90. Найдите геометрическое место точек, для каждой из которых сумма или разность расстояний до данной точки и до данной прямой есть величина постоянная.
91. Эллипс с полуосями а и b перемещен так, что его центр совпал с точкой  , а оси остались параллельными осям координат. Какое уравнение имеет эллипс в своем новом положении?
, а оси остались параллельными осям координат. Какое уравнение имеет эллипс в своем новом положении?
92. Напишите уравнение эллипса, пересекающего ось  в точках
в точках  ,
, 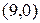 и касающегося оси
и касающегося оси  в точке (0,3), зная, что его оси параллельны осям координат.
в точке (0,3), зная, что его оси параллельны осям координат.
93. Напишите уравнение эллипса, оси которого параллельны осям координат, если он касается осей  и
и  соответственно в точках
соответственно в точках  и
и 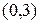 .
.
94. Эллипс касается оси ординат в начале координат, а центр его находится в точке  Составьте уравнение эллипса, зная, что его эксцентриситет е равен
Составьте уравнение эллипса, зная, что его эксцентриситет е равен  .
.
95. Составьте уравнение эллипса, фокусы которого имеют координаты 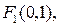
 а большая полуось равна
а большая полуось равна  .
.
96. Напишите уравнение эллипса с полуосями 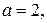
 для которого прямые
для которого прямые 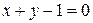 и
и  суть соответственно большая и малая оси.
суть соответственно большая и малая оси.
97. Эллипс при движении по плоскости касается двух взаимно перпендикулярных прямых. Какую линию описывает центр эллипса?
98. Напишите уравнение гиперболы, проходящей через точку 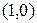 , если известно, что ее асимптотами являются прямые
, если известно, что ее асимптотами являются прямые  и
и 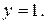
99. Составьте уравнение гиперболы, фокусы которой имеют координаты 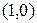 ,
,  , а асимптоты параллельны осям координат.
, а асимптоты параллельны осям координат.
100. Докажите, что уравнение 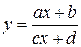 , где
, где 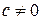 и
и  , задает на координатной плоскости равностороннюю гиперболу. Найдите ее фокусы.
, задает на координатной плоскости равностороннюю гиперболу. Найдите ее фокусы.
101. Напишите уравнение равносторонней гиперболы, зная ее фокус  и асимптоту
и асимптоту 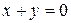 .
.
102. Напишите уравнение равносторонней гиперболы, зная ее фокус  и асимптоту
и асимптоту  .
.
103. Составьте уравнение гиперболы, зная один из ее фокусов 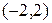 и асимптоты
и асимптоты  ,
, 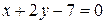 .
.
104. Составьте уравнение параболы, зная, что фокус имеет координаты: а)  б)
б) 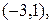 а ось ординат служит директрисой.
а ось ординат служит директрисой.
105. Определите фокус параболы 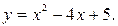
106. Составьте уравнение параболы, зная, что ее вершина имеет координаты  фокальный параметр равен p и направление оси симметрии совпадает:
фокальный параметр равен p и направление оси симметрии совпадает:
1) с положительным направлением оси  ;
;
2) с отрицательным направлением оси  ;
;
3) с положительным направлением оси  ;
;
4) с отрицательным направлением оси  .
.
107. Напишите уравнение параболы, вершина которой находится в точке  а ось параллельна оси
а ось параллельна оси  , зная, что на оси
, зная, что на оси  эта парабола отсекает хорду длины
эта парабола отсекает хорду длины 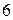 .
.
108. Докажите, что параболы, имеющие общий фокус и совпадающие, но противоположно направленные оси, пересекаются под прямым углом (т.е. касательные, проведенные к ним в каждой точке их пересечения, взаимно перпендикулярны).
109. Напишите уравнение параболы, касающейся оси  в точке
в точке 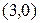 , а оси
, а оси  в точке
в точке 
110. Напишите уравнение параболы, проходящей через точки 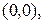
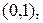 осью которой служит прямая
осью которой служит прямая  .
.
111. Напишите уравнение параболы, зная ее директрису  и фокус
и фокус 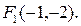
112. Напишите уравнение параболы, вершина которой находится в начале координат, а фокус – в точке 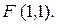
113. Составьте уравнение линии второго порядка, зная ее фокус 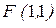 , директрису
, директрису  и эксцентриситет
и эксцентриситет  .
.
114. Составьте уравнение линии второго порядка, зная ее фокусы 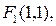
 и одну из ее директрис
и одну из ее директрис 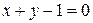 .
.
115. Составьте уравнение линии второго порядка, зная ее фокус 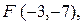 центр
центр  и одну из директрис
и одну из директрис  .
.
116. Определите вид следующих линий второго порядка (система координат аффинная):
1) 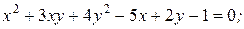
2) 
3) 
4) 
5) 
6) 
117. Покажите, что каждое из нижеследующих уравнений определяет пару прямых, и найдите уравнения этих прямых (система координат аффинная):
1) 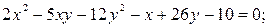
2) 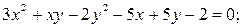
3) 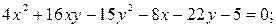
4) 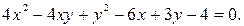
118. Используя параллельный перенос, выяснить вид и расположение на координатной плоскости следующих линий второго порядка:
1) 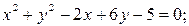
2) 
3) 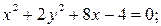
4) 
5) 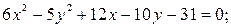
6) 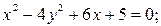
7) 
8) 
9) 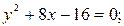
10) 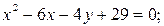
11) 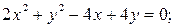
12) 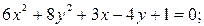
13) 
14) 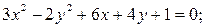
15) 
16) 
17) 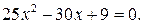
119. Линия второго порядка определяется уравнением 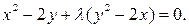 Определите тип линии при каждом вещественном значении параметра
Определите тип линии при каждом вещественном значении параметра  и описать ее расположение относительно данной системы координат.
и описать ее расположение относительно данной системы координат.
120. При каком необходимом и достаточном условии уравнение 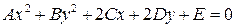 задает: 1) эллипс; 2) гиперболу? Система координат аффинная.
задает: 1) эллипс; 2) гиперболу? Система координат аффинная.
121. Используя метод вращений, определите форму и расположение на плоскости следующих линий второго порядка:
1) 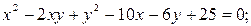
2) 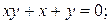
3) 
4) 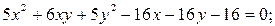
5) 
6) 
7) 
8) 
9) 
10) 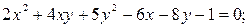
11) 
12) 
13) 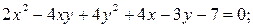
14) 
122. Линия второго порядка определяется уравнением  Определите вид линии при каждом вещественном значении параметра
Определите вид линии при каждом вещественном значении параметра  и описать ее расположение относительно данной системы координат.
и описать ее расположение относительно данной системы координат.
Дата добавления: 2015-07-11; просмотров: 575 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Кривые Энгеля | | | Эллипс. |