ЗАДАНИЕ №4 Решить следующие задачи

Вариант 1. Составить уравнение директрисы параболы у²=8х.

Вариант 2. Найти фокус и эксцентриситет эллипса 5x²+9y²=45.

Вариант 3. Составить уравнение окружности с центром в точке А(-3;0) и радиусом равным R=5.

Вариант 4. Дан эллипс 4x²+2y²=2. Найти его полуоси.

Вариант 5. Составить уравнение гиперболы, если большая полуось а=4, а фокусное расстояние с=5.

Вариант 6. Составить уравнение параболы, симметричной относительно оси ОУ и проходящей через точку А(2;24).

Вариант 7. Найти уравнение параболы, если она симметрична относительно оси ОУ, проходит через точку М(6;3) и начало координат.

Вариант 8. Составить уравнение гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами 8.

Вариант 9. Написать уравнение гиперболы, если действительная полуось равна 5, а эксцентриситет 2,6.

Вариант 10. Составить уравнение эллипса, если малая ось равна 10, расстояние между фокусами равно 8.

Вариант 11. найти уравнение эллипса, если малая полуось равна 12, а эксцентриситет 5/13.

Вариант 12. Даны две точки А(4;2) и в(12;8). Составить уравнение окружности, диаметр которой отрезок АВ.

Вариант 13. Найти полуоси, уравнения асимптот и эксцентриситет гиперболы 9х²-16у²=144.

Вариант 14. Найти координаты фокуса и уравнение директрисы параболы у²=12х.

Вариант 15. Составить уравнение гиперболы, зная, что расстояние между директрисами равно 4, а расстояние между фокусами 16.

Вариант 16. Найти полуоси, фокусы и эксцентриситет эллипса 4х²+9у²=16.

Вариант 17. Найти координаты центра и радиус окружности х²+у²-4х+8у-16=0.

Вариант 18. Найти уравнение гиперболы, если расстояние между фокусами равно 10, эксцентриситет 5/3.

Вариант 19. Найти длины осей, фокусы, уравнение асимптот, эксцентриситет гиперболы 144х²-25у²=3600.

Вариант 20. Определить длины осей, фокусы и эксцентриситет эллипса 9х²+у²=36.

Вариант 21. Составить уравнение параболы, симметричной относительно оси ОУ и проходящей через точку А(2;24).

Вариант 22. Найти уравнение параболы, если она симметрична относительно оси ОУ, проходит через точку М(6;3) и начало координат.

Вариант 23. Составить уравнение гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами 8.

Вариант 24. Написать уравнение гиперболы, если действительная полуось равна 5, а эксцентриситет 2,6.

Вариант 25. Составить уравнение эллипса, если малая ось равна 10, расстояние между фокусами равно 8.

Вариант 26. найти уравнение эллипса, если малая полуось равна 12, а эксцентриситет 5/13.

Вариант 27. Даны две точки А(4;2) и в(12;8). Составить уравнение окружности, диаметр которой отрезок АВ.

Вариант 28. Найти полуоси, уравнения асимптот и эксцентриситет гиперболы 9х²-16у²=144.

Вариант 29. Найти координаты фокуса и уравнение директрисы параболы у²=12х.

Вариант 30. Составить уравнение гиперболы, зная, что расстояние между директрисами равно 4, а расстояние между фокусами 16.

ЗАДАНИЕ №5 Решить следующие задачи:

Вариант 1. Найти длины осей, фокусы, уравнение асимптот, эксцентриситет гиперболы 144х²-25у²=3600.

Вариант 2. Найти фокус и эксцентриситет эллипса 5x²+9y²=45.

Вариант 3. Составить уравнение окружности с центром в точке А(-3;0) и радиусом равным R=5.

Вариант 4. Составить уравнение гиперболы, если большая полуось а=4, а фокусное расстояние с=5.

Вариант 5. Составить уравнение параболы, симметричной относительно оси ОУ и проходящей через точку А(2;24).

Вариант 6. Дан эллипс 4x²+2y²=2. Найти его полуоси.

Вариант 7. Найти уравнение параболы, если она симметрична относительно оси ОУ, проходит через точку М(6;3) и начало координат.

Вариант 8. Составить уравнение гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами 8.

Вариант 9. Написать уравнение гиперболы, если действительная полуось равна 5, а эксцентриситет 2,6.

Вариант 10. Составить уравнение эллипса, если малая ось равна 10, расстояние между фокусами равно 8.

Вариант 11. Составить уравнение директрисы параболы у²=8х.

Вариант 12. найти уравнение эллипса, если малая полуось равна 12, а эксцентриситет 5/13.

Вариант 13. Даны две точки А(4;2) и в(12;8). Составить уравнение окружности, диаметр которой отрезок АВ.

Вариант 14. Найти уравнение параболы, симметричной относительно оси ОХ, и проходящей через точку А(5;15)

Вариант 15. Найти координаты фокуса и уравнение директрисы параболы у²=12х.

Вариант 16. Составить уравнение гиперболы, зная, что расстояние между директрисами равно 4, а расстояние между фокусами 16.

Вариант 17. Найти полуоси, фокусы и эксцентриситет эллипса 4х²+9у²=16.

Вариант 18. Найти координаты центра и радиус окружности х²+у²-4х+8у-16=0.

Вариант 19. Найти уравнение гиперболы, если расстояние между фокусами равно 10, эксцентриситет 5/3.

Вариант 20. Найти полуоси, уравнения асимптот и эксцентриситет гиперболы 9х²-16у²=144.

Вариант 21. Определить длины осей, фокусы и эксцентриситет эллипса 9х²+у²=36.

Вариант 22. Составить каноническое уравнение эллипса, если малая полуось равна 15, F(-10,0).

Вариант 23. Составить уравнение гиперболы, имеющей эксцентриситет равный , проходящей через точку А(-5;0).

Вариант 24. Составить уравнение параболы, если уравнение директрисы этой параболы имеет вид у=-4.

Вариант 25. Составить уравнение эллипса, проходящего через точки А(- ; 1/3) и В(; ).

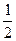Вариант 26. Составить уравнение гиперболы, если уравнение соответствующих асимптот имеют вид у= х, расстояние между фокусами равно 12.

Вариант 27. Составить уравнение эллипса, если малая полуось равна 2 , эксцентриситет равен 7/9.

Вариант 28. Составить уравнение параболы, если уравнение директрисы этой параболы имеет вид х=-2

Вариант 29. Гипербола проходит через точки А(3,- ) и В(,6). Найти уравнение этой гиперболы.

Вариант 30. Большая ось эллипса равна 50, эксцентриситет равен 3/5. Составить уравнение эллипса.

ЗАДАНИЕ №6 Решить следующие задачи:

Вариант 1. Составить уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса

Вариант 2. Найти уравнение гиперболы, проходящей через точку (10; 3 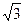), если ее асимптоты даны уравнениями y= x.

Вариант 3. Эллипс, симметричный относительно осей координат, проходит через точки М₁(4; 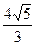) и М₂(0;4). Найти полуоси, координаты фокусов и эксцентриситет эллипса.

Вариант 4. Найти уравнение гиперболы, фокусы которой лежат на оси ОХ, расстояние между фокусами равно 10, а уравнения асимптот y= x.

Вариант 5. Эллипс проходит через точку М(1;1) имеет эксцентриситет равный 3/5. Составить уравнение эллипса

Вариант 6. Найти уравнение эллипса, у которого сумма полуосей a+b=27, а расстояние между фокусами 2с=18.

Вариант 7. Найти уравнение параболы, которая проходит через точки пересечения прямой x-y=0 и окружности x²+y²-4y=0 и симметрична относительно оси ОУ.

Вариант 8. На эллипсе найти точку, равноудаленную от центра и правого фокуса, и определить ее расстояние от этих точек.

Вариант 9. Найти уравнение окружности, проходящей вершину гиперболы х²-16у²=64, имеющей вершину в точке А(0;-2).

Вариант 10. Найти периметр треугольника, вершинами которого служат вершина параболы у²= х, ее фокус и точка на параболе, ордината которой равна -4.

Вариант 11. Найти уравнение параболы, у которой вершина лежит в начале координат, направление оси симметрии совпадает с отрицательным направлением оси ОХ, параметр р равен расстоянию от фокусов гиперболы до ее асимптот.

Вариант 12. Найти уравнение окружности, центр которой находится в точке М(2;-3) и которая касается прямой 4х+3у-19=0.

Вариант 13. Составить уравнение окружности касающейся оси ОХ и проходящей через точки А(0;8) и В(7;1).

Вариант 14. Записать уравнение окружности, проходящей через левый фокус гиперболы 3х²-5у²=30 с центром в точке А(0;6).

Вариант 15. На параболе у²=8х найти точку, расстояние которой от директрисы равно 4.

Вариант 16. Найти уравнение гиперболы, вершина и фокусы которых находятся в соответствующих фокусах и вершинах эллипса

Вариант 17. Найти уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой у-х=0 и окружности х²+у²+8х=0 и симметрична относительно оси ОХ.

Вариант 18. Составить уравнение окружности, проходящей через точки А(5;0) и В(1;4), если центр ее лежит на прямой х+у-3=0.

Вариант 19. Составить уравнение окружности, проходящей через точки А(1;2), В(0;1), С(-3;0).

Вариант 20. Эксцентриситет гиперболы равен . Составить уравнение гиперболы, проходящей через точку М (; ).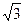

Вариант 21. Составить уравнение гиперболы, проходящей через точку М(9;8), если асимптоты гиперболы имеют уравнения y= x.

Вариант 22. Составить уравнение параболы, имеющей вершину в начале координат, если известно, что ее фокус находится в точке пересечения прямой 4х-3у-4=0 с осью ОХ.

Вариант 23. Парабола у²=2х осекает от прямой, проходящей через начало координат, хорду, длина которой равна ¾. Составить уравнение этой прямой.

Вариант 24. Найти уравнение окружности, проходящей фокусы эллипса 16х²+41у²=656 и имеющей центр в нижней вершине эллипса.

Вариант 25. На параболе у²=32х найти точку, расстояние которой от прямой 4х+3у+10=0 равно 2.

Вариант 26. На прямой х+5=0 найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса .

Вариант 27. Найти уравнение прямой, проходящей через правый фокус эллипса х²+4у²=12 и точку А(2;-8).

Вариант 28. На эллипсе найти точку, равноудаленную от центра и правого фокуса, и определить ее расстояние от этих точек.

Вариант 29. Найти уравнения параболы и ее директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси ОХ и что точка пересечения прямых у=х и х+у-2=0 лежит на параболе.

Вариант 30. Составить уравнение прямой проходящей через центры окружностей х²+у²=5 и х²+у²+2х+4у-31=0.

Дата добавления: 2015-07-11