Моментные гидроцилиндры

На рис. 4 показана схема моментного (лопастного или поворотного) гидроцилиндра.

При подаче жидкости под рабочим давлением p в левую полость гидроцилиндра под действием этого давления происходит поворот лопасти, закреплённой на валу, по часовой стрелке, а из правой полости жидкость вытесняется на слив. Для движения в обратном направлении линии подачи и слива меняются местами.

Уравнения равновесия для прямого и обратного хода запишутся так:

Т_п = М_п + Т_п.ин +Т_п.пд + Т_п.тр, Т_о = М_о + Т_о.ин +Т_о.пд + Т_о.тр,

где Т_п и Т_о – движущие моменты прямого и обратного хода,

М_п и М_о – полезная нагрузка прямого и обратного хода,

Т_п.ин и Т_о.ин – моменты сил инерции прямого и обратного хода,

Т_п.пд и Т_о.пд – моменты сил противодавления прямого и обратного хода,

Т_п.тр и Т_о.тр – моменты сил трения уплотнений лопасти и вала прямого и обратного хода.

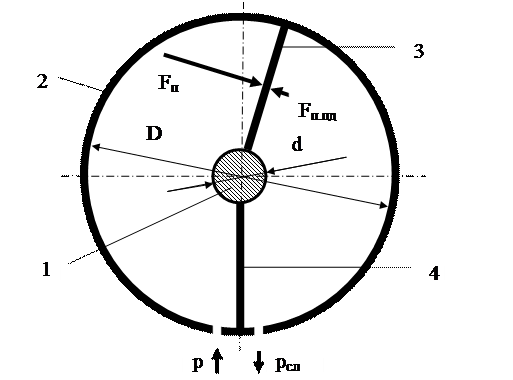
Рис. 4. Схема моментного гидроцилиндра: 1 – вал; 2 – корпус цилиндра; 3 –лопасть; 4 – перегородка

Ввиду симметричности моментных гидроцилиндров, т. е. равенства площадей лопасти в обеих полостях, движущие моменты, моменты сил противодавления и сил трения одинаковы по величине при повороте в обе стороны. Кроме этого, замечено, что в большинстве случаев полезная нагрузка существенно больше инерционной. Поэтому расчёт моментного гидроцилиндра можно провести по параметрам только того хода, при котором полезная нагрузка выше. Пусть М_п > М_о. Тогда расчёт ведется по параметрам прямого хода.

Движущий момент

Т_п = F_п ∙ (D + d) / 4, где F_п = p ∙ (D – d) ∙ b /2.

Окончательно получается

Т_п= p ∙ (D² – d²) ∙ b / 8.

Аналогично запишется момент сил противодавления:

Т_п.пд= p_сл ∙ (D² – d²) ∙ b / 8,

где b – длина лопасти цилиндра, а момент сил инерции

Т_п.ин = I ∙ 2 ∙ ω _п / t_п.

Учёт влияния сил трения в моментных гидроцилиндрах часто проводят с помощью коэффициента полезного действия η. Тогда уравнение равновесия можно записать так:

Δ p ∙ (D² – d²) ∙ b ∙ η / 8 = М_п + I ∙ 2 ∙ ω _п / t_п,

где Δp = p – p_сл.

Величины правой части этого уравнения известны. Из величин левой части выбираются Δp, η и b = k ∙ D, k выбирается, исходя из желаемого соотношения длины и диаметра цилиндра, а d определяется по условию прочности вала при кручении. Тогда в уравнении остаётся одна неизвестная величина D и уравнение приобретает вид

D³ + p ∙ D +q = 0,

действительный корень которого находится следующим образом:

Q = (p/3)³ + (q/2)², A = (-q/2 +Q^1/2)^1/3, B = (-q/2 -Q^1/2)^1/3,

D = A+B.

Далее вычисляется b и принимаются значения b и D, ближайшие к значениям стандартного ряда размеров, после чего проводится проверка

работоспособности цилиндра в заданных условиях по отношению

Δ p ∙ (D² – d²) ∙ b ∙ η / 8 ≥ М_п + I ∙ 2 ∙ ω _п / t_п.

При истинности данного отношения найденные параметры цилиндра можно принять, в противном случае следует увеличить D и (или) b и (или) p, а затем снова провести проверку.

Пример. Определить основные размеры моментного гидроцилиндра, полезная нагрузка на вал которого М_п = 2000 Нм, момент инерции массы поворачиваемых частей механизма, приведённый к валу двигателя, I =20 кгм², частота вращения n = 10 об/мин и время разгона до неё 0,1 с, разность давлений в полостях двигателя Δp = 4 МПа, коэффициент полезного действия двигателя η = 0,9.

Расчёт начинаем с определения диаметра вала из условия его прочности при кручении. Вал нагружается моментами полезной нагрузки и сил инерции.

Т = М_п + I ∙ 2 ∙ ω _п / t_п = 2000 + 2 ∙ 20 ∙ 3,14 ∙ 10 /30 / 0,1 = 2419 Нм.

Пусть допускаемое напряжение при кручении материала вала [τ ] = 200 МПа. Тогда минимальный диаметр вала

d = (16 ∙ Т / π / [τ ])^0,333 = (16 ∙ 2419 / 3,14 /200000000)^0,333 = 0,0395 м.

Принимаем диаметр вала внутри цилиндра d = 50 мм.

По условиям компоновки гидроцилиндра в конструкции выбирается соотношение его диаметра и длины (ширины лопасти). Пусть k = 0,5, тогда b = 0,5∙ D. Теперь подставим известные величины в выражение

Δ p ∙ (D² – d²) ∙ b ∙ η / 8 = М_п + I ∙ 2 ∙ ω _п / t_п,

4 ∙ (D² – 50²) ∙ 0,5 ∙ D ∙ 0,9 / 8 = 2419 ∙ 10³. (Здесь размеры в мм, давление в МПа(Н / мм²), момент в Нмм).

После преобразования получаем

D³ – 2500D – 10,751∙ 10⁶ = 0.

Решаем кубическое уравнение

Q = (- 2500 / 3)³ + (- 10,751 ∙ 10⁶ / 2)² = 28,895 ∙ 10¹²,

А = (10,751 ∙ 10⁶ / 2 + (28,895 ∙ 10¹²)^0,5)^0,333 = 220,7,

В = (10,751 ∙ 10⁶ / 2 - (28,895 ∙ 10¹²)^0,5)^0,333 = 3,78,

D = 220,7 + 3,78 = 224,48 мм.

Принимаем ближайшее бóльшее стандартное значение D = 225 мм.

b = 0,5 ∙ 225 = 112,5, принимаем b = 125 мм.

Проверка работоспособности цилиндра проводится так же, как поступательных цилиндров двустороннего действия, но, естественно, с использованием соответствующих параметров вращательного движения.

Дата добавления: 2015-07-11