Определение коэффициента гидравлического трения

Глава 5. КОЭФФИЦИЕНТ ГИДРАВЛИЧЕСКОГО ТРЕНИЯ

В ТЕХНИЧЕСКИХ ТРУБАХ

Определение коэффициента гидравлического трения

Технические трубы – это трубы с естественной шероховатостью стенок, обусловленной материалом стенок, технологией изготовления, условиями эксплуатации и т.д.

Эквивалентная шероховатость D_э – это высота выступа воображаемой равнозернистой поверхности, при которой потери напора такие же, как и для реальной шероховатости. D_э определяется экспериментально.

Потери напора для любого режима движения жидкости выражаются формулой Дарси-Вейсбаха:

.

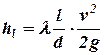Формулу Дарси-Вейсбаха можно привести к виду:

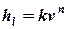, (1)

где k – коэффициент пропорциональности, v – средняя скорость течения, n – показатель степени.

Для определения режима течения определяется число Рейнольдса:

.

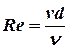Для ламинарного режима число Рейнольдса Re < 2300. Коэффициент Дарси определяется по теоретической формуле или по уточненной экспериментальной формуле 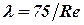. Потери напора пропорциональны первой степени средней скорости, т.е. n = 1 в (1), а коэффициент Дарси зависит от числа Рейнольдса .

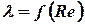Для турбулентного режима течения при Re > 2300 в зависимости от высоты выступов шероховатости и толщины вязкого подслоя различают три области сопротивления.

Области гладких труб соответствует диапазон чисел Рейнольдса 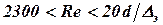. Отношение 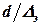называют относительной шероховатостью. Для вычисления коэффициента Дарси используют формулу Г. Блаузиса:

.

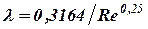Здесь 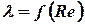, как и для ламинарного режима, а потери напора пропорциональны скорости в степени n = 1,75. График 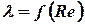для ламинарного режима и области гладких труб приведен на рисунке.

Переходная (доквадратичная) область соответствует диапазону 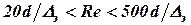. Для коэффициента Дарси используется формула А.Д. Альтшуля:

.

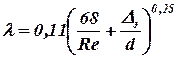Здесь 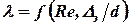. Показатель степени в (1) равен 1,75 < n < 2.

Область совершенно (абсолютно) шероховатых труб имеет место при 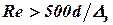. Для коэффициента Дарси используется формула Б.Л. Шифринсона:

.

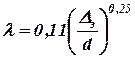Здесь коэффициент гидравлического трения зависит только от относительной шероховатости 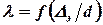, а потери напора пропорциональны квадрату скорости, поэтому область называется квадратичной.

Формула А.Д. Альтшуля является универсальной. При 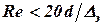она практически совпадает с формулой Г. Блаузиса, а при 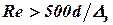- с формулой Б.Л. Шифринсона.

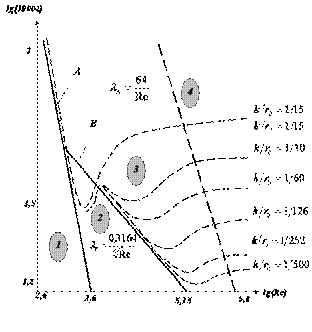Экспериментальным изучением влияния числа Рейнольдса и относительной шероховатости занимался Никурадзе И. И., который проводил опыты для диапазонов 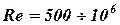и .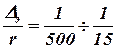

Результаты этих исследований сведены к графику в логарифмических координатах.

Выводы из графиков Никурадзе:

1. При ламинарном течении шероховатость практически не влияет на сопротивление. Эксперимент практически полностью подтверждает с теоретические формулы.

2. Критическое число Рейнольдса от шероховатости не зависит (штриховые кривые отклоняются от прямой A в одной точке).

3. В области турбулентных течений при небольших числах Рейнольдса и малой шероховатости сопротивление от шероховатости не зависит (штриховая линия совпадает с прямой B), а с увеличением Re сопротивление возрастает.

4. При больших значениях чисел Рейнольдса l перестаёт зависеть от Re и становится постоянным для определённой относительной шероховатости.

Дата добавления: 2015-07-11