Читайте также:
|
В силу безусловного приоритета двоичной системы счисления при внутреннем представлении информации в компьютере кодирование «внешних» символов основывается на сопоставлении каждому из них определенной группы двоичных знаков. При этом из технических соображений и из соображений удобства кодирования-декодирования следует пользоваться равномерными кодами, т.е. двоичными группами равной длины.
Попробуем подсчитать наиболее короткую длину такой комбинации с точки зрения человека, заинтересованного в использовании лишь одного естественного алфавита - скажем, английского: 26 букв следует умножить на 2 (прописные и строчные) - итого 52; 10 цифр, будем считать, 10 знаков препинания; 10 разделительных знаков (три вида скобок, пробел и др.), знаки привычных математических действий, несколько специальных символов (типа #, $, & и др.) - итого - 100. Точный подсчет здесь не нужен, поскольку нам предстоит решить простейшую задачу: имея, скажем, равномерный код из групп по N двоичных знаков, сколько можно образовать разных кодовых комбинаций. Ответ очевиден: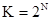 
. Итак, при N=6 К = 64 -явно мало, при N = 7 К = 128 -вполне достаточно.
Однако, для кодирования нескольких (хотя бы двух) естественных алфавитов (плюс все отмеченные выше знаки) и этого недостаточно. Минимально достаточное значение Nв этом случае 8; имея 256 комбинаций двоичных символов, вполне можно решить указанную задачу. Поскольку 8 двоичных символов составляют 1 байт, то говорят о системах «байтового» кодирования.
Дата добавления: 2015-07-11; просмотров: 227 | Нарушение авторских прав