Алгоритм Сугено.

Алгоритм Сугено применяется, когда известна не форма функции соответствия выходного параметра, а весовые коэффициенты, через которые входные параметры вносят свою «лепту». При для разных нечётких множеств A1,A2,A3; B1,B2,В3; C1,C2,C3 значений входных параметров a,b,c применяются свои коэффициенты. Правила выглядят так:

– правило 1: если a∈A1 & b∈B1, то c = ka1a + kb1b;

– правило 2: если a∈А2 & b∈B2, то c = ka2a + kb2b;

и т.д для других входных параметров.

В отличие от алгоритма Мамдани, не используются правила, содержащие дизъюнкции в левых частях импликаций.

Шаг1: дефаззификация. На этом шаге по чётким значениям входных параметров a0 и b0 определяют значения функций соответствия µA1(a0), µB1(b0), µA2(a0), µB2(b0) (и так далее для других параметров). Затем определяют уровни отсечения выхода:

µ1 = min(µA1(a0), µB1(b0));

µ2 = min(µA2(a0), µB2(b0)).

И так далее для других входных параметров.

Шаг2: находят индивидуальные результаты выполнения правил:

c1 = ka1a0 + kb1b0;

c2 = ka2a0 + kb2b0;

И так далее для других входных параметров.

Шаг3: по c1, с1 µ1, µ2 и т.д. находят выход по методу дискретного ЦТ, как и в алгоритме Цукамото: в числителе сумма произведений сiµi, в знаменателе – сумма µi.

Чтобы построить НЛК Сугено, если неизвестны весовые коэффициенты, экспериментально изменяют каждый входной параметр по отдельности, зафиксировав остальные, и смотрят, как изменяется выходной параметр. Находят интервал, в котором изменение выходного параметра можно аппроксимировать линейной зависимостью от входного параметра в пределах приемлемой погрешности. Этот i-ый интервал образует одно из подмножеств Ai параметра a. И так далее для остальных параметров.

Алгоритм Сугэно (0-го порядка). Исходный набор правил представляется в виде

П_i: если x есть A_i, тогда z есть z_i, i = 1,2,…,n,

где z_i = z(x_i).

Алгоритм состоит всего из двух этапов. Первый этап идентичен первому этапу алгоритма Мамдани. На втором этапе находится (четкое) значение переменной вывода:

.

Возможность использования аппарата нечеткой логики для задач аппроксимации базируется на следующих результатах.

1. В 1992 г. Ванг (Wang) показал, что нечеткая система, использующая набор правил

П_i: если x_i есть A_i и y_i есть B_i, тогда z_i есть C_i, i = 1,2,…,n

при

1) гауссовских функциях принадлежности

, , ,

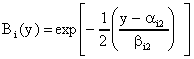2) композиции в виде произведения

[A_i(x) and B_i(y)] = A_i(x)B_i(y),

3) импликации в форме (Larsen)

[A_i(x) and B_i(y)]®C_i(z) =A_i(x)B_i(y)C_i(z),

4) центроидном методе приведения к четкости

,

где c_i - центры C_i(z), является универсальным аппроксиматором, т.е. может аппроксимировать любую непрерывную функцию на компакте U с произвольной точностью (естественно, при ).

Иначе говоря, Ванг доказал теорему: для каждой вещественной непрерывной функции F(X), заданной на компакте U и для произвольного e>0 существует нечеткая экспертная система, формирующая выходную функцию (X) такую, что

,

где 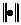- символ принятого расстояния между функциями.

2. В 1995 году Кастро (Castro) показал, что логический контроллер Мамдани при

1) симметричных треугольных функциях принадлежности:

2) композиции с использованием операции min:

[A_i(x) and B_i(y)] = min{A_i(x),B_i(y)},

3) импликации в форме Мамдани и центроидного метода приведения к четкости

,

также является универсальным аппроксиматором.

Сравнение описанных алгоритмов выполнялось при следующих условиях:

· аппроксимации функции проводилась на отрезке [-1, 1];

· аппроксимируемая функция задавалась набором значений (x_i, z_i), i = 1,2,…,n, при этом точки z_i располагались эквидестантно;

· функции принадлежности имели вид функций Гаусса, т.е. (x) =j((x-x_i)/a), 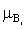(z) = j((z-z_i)/b), где j(·) - функция Гаусса, j(s/s) = exp(-s²/2s²), s - параметр функции (соответственно, a или b).

· количество правил n задавалось a priori;

· значения параметров a и b варьировались для получения наилучшего качества аппроксимации при заданном n.

Реализация алгоритмов и соответствующие вычислительные эксперименты проводилась с помощью системы MathCAD 2000.

Некоторые результаты при n = 9, a = 0.1, b = 0.3 приведены в табл. 1 и 2.

Таблица 1. Результаты аппроксимации для функции F(x) = x²

i
xi	-1	-0.75	-0.5	-0.25		0.25	0.5	0.75
zi	1.000	0.563	0.250	0.063		0.063	0.25	0.563	1.000
Оценка по алгоритму Мамдани	0.973	0.570	0.257	0.070	0	0.070	0.257	0.570	0.973
Оценка по алгоритму Сугэно	0.982	0.568	0.255	0.068	0	0.068	0.255	0.568	0.982

Таблица 2. Результаты аппроксимации для функции F(x) = x³

i
xi	-1	-0.75	-0.5	-0.25		0.25	0.5	0.75
zi	-1.000	-0.422	-0.125	-0.016		0.016	0.125	0.422	1.000
Оценка по алгоритму Мамдани	-0.962	-0.441	-0.136	-0.021	0	0.021	0.136	0.441	0.962
Оценка по алгоритму Сугэно	-0.976	-0.433	-0.133	-0.019	0	0.019	0.133	0.433	0.976

Приведенные и другие аналогичные результаты (полученные для большого числа вариантов) позволяют сделать выводы:

1) при прочих равных условиях и при оптимальных параметрах a и b погрешность аппроксимации с применением алгоритма Сугэно несколько меньше, чем с применением алгоритма Мамдани;

2) алгоритм Сугэно с вычислительной точки зрения реализуется значительно проще, чем алгоритм Мамдани, а время счета для него меньше, чем для алгоритма Мамдани в 50-100 раз;

3) общий вывод: если нет каких-либо особенных доводов в пользу алгоритма Мамдани, то лучше использовать не его, а алгоритм Сугэно.

Данные выводы, разумеется, носят предварительный характер и нуждаются в более корректном подтверждении (для функций многих переменных и т.п.).

В заключение приведем еще один результат, устанавливающий связь между алгоритмом Сугэно, так называемой обобщенно-регрессионной нейронной сетью (GRNN) и непараметрической оценкой регрессии Надарая-Ватсона [2].

Указанная сеть предназначена для решения задач регрессии (аппроксимации), при этом ее выход формируется как взвешенное среднее выходов по всем обучающим наблюдениям:

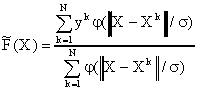, (1)

где X^k, y^k - точки обучающей выборки (X - в общем случае векторный аргумент); j(·) - отмеченная функция Гаусса.

Поясним данную формулу и название сети.

Предположим, что элементы обучающей выборки - случайные величины, с совместной плотностью вероятности p₂(X,y), при этом, как известно, условное математическое ожидание M(y/X) называется регрессией (обобщенной регрессией) и определяется соотношением

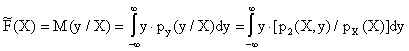, (2)

где - условная плотность вероятности y по X, - безусловная плотность вероятности случайной величины X.

Примем в последнем выражении аппроксимации:

, ,

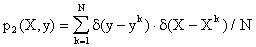где d(·) - обозначение дельта-функции Дирака.

Подстановка данных аппроксимаций в (2) дает:

.

Изменение порядка выполнения операций интегрирования и суммирования (здесь это допустимо и корректно) и использование, далее, свойств дельта-функции позволяет записать:

.

Аппроксимация теперь дельта-функции функцией Гаусса приводит к выше представленному выражению для выхода обобщенно-регрессионной нейронной сети; приведенный вывод собственно и поясняет ее название.

Но, если в формуле (1) принять обозначения z_k = y^k и a_k = j ((X - X^k)/s), то функционирование такой сети формально можно считать подобным функционированию системы, реализующей приведенный алгоритм Сугэно 0-го порядка (упрощенный алгоритм нечеткого вывода [1]), при этом величины a_k в данном случае - степени "истинности" продукционных правил при заданных (гауссовых) функциях принадлежности j(·) и значении переменной входа, равной X^k.

Более того, выражение (1), описывающее, как установлено, выход сети GRNN и алгоритма нечеткого вывода Сугэно, полностью совпадает с непараметрической оценкой регрессии, известной как оценка Надарая-Ватсона, для которой доказана следующая теорема о сходимости [2].

Теорема. Оценка, определяемая формулой (1), если j(·) - функция Гаусса, при выполнении условий

N®Ґ, s_N®0, N ®0

где s_N - параметр функции Гаусса, в данном случае зависящий от объема обучающей выборки, m - размерность вектора X,

сходится к F(X) с вероятностью 1.

Приведенный результат является теоретическим обоснованием алгоритма Сугэно как универсального аппроксиматора.

Дата добавления: 2015-07-11