Краткая теория. Определение коэффициента теплопроводности металлов

Определение коэффициента теплопроводности металлов

Цель работы: ознакомление с теорией теплопроводности в твёрдом теле, определение коэффициента теплопроводности калориметрическим методом.

Оборудование: прибор для определения коэффициента теплопроводности, термометры, секундомер, мензурка.

Краткая теория

Рассмотрим два теплоизолированных тела (например, два алюминиевых стаканчика с водой (рис.1)), соединённых между собой однородным теплопроводящим (металлическим) стержнем с изолированной боковой поверхностью. Начальные температуры этих тел равны соответственно Т₁₀ и Т₂₀. По истечении некоторого времени в стержне возникает равномерное падение температуры, при котором поток тепла не будет изменяться вдоль стержня. Температуры тел через некоторый промежуток времени Dt равны соответственно Т₁ и Т₂. Пусть Т₁ > Т₂. Поток тепла вдоль стержня от тела 1 к телу 2 через поперечное сечение стержня площади S и длины L равен:

или (1)

Здесь c - коэффициент теплопроводности стержня.

Считая теплоёмкости С₁ и С₂ тел постоянными, запишем уравнения (1) в виде:

и (2)

Выразим из уравнений (2) быстроту изменения темперы тел:

(3)

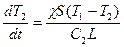и (4)

Вычтем из уравнения (3) уравнение (4), получим

(5)

Обозначим через 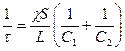(6)

Здесь t имеет размерность времени. Используя обозначение (6), можно переписать уравнение (5) в виде:

(7)

Это уравнение с разделяющимися переменными, проинтегрируем его и получим:

(8)

Следовательно, разность температур убывает во времени по экспоненциальному закону. За время t эта разность убывает в е раз (е – основание натурального логарифма). Поэтому t характеризует время установления равновесия между телами 1 и 2 (время релаксации). Постоянную А найдём из начальных условий: Т₁ = Т₁₀ и Т₂ = Т₂₀ при t=0. С учётом этого или

(9)

Прологарифмируем уравнение (9) и получим:

(10)

Подставим в уравнение (10) вместо 1/t правую часть уравнения (6) и получим:

. Отсюда найдём коэффициент теплопроводности:

(11)

Если теплоёмкости тел 1 и 2 одинаковы (С₁=С₂=С), то коэффициент теплопроводности равен:

(12)

Дата добавления: 2015-07-11