Гидравлический расчет коротких трубопроводов

Принципиальный подход к расчету коротких трубопроводов тот же, что и к расчету длинных: необходимо составить уравнение Бернулли для сечения, проведенного через питающий водоем, и конечного сечения трубопровода.

При этом, конечно, необходимо учитывать особенности, отличающие баланс энергии в коротких трубопроводах от баланса энергии в длинных трубах. Наиболее важное отличие состоит в том, что существенное место в балансе энергии коротких трубопроводов составляют потери энергии на местных сопротивлениях. Кроме того, при расчетах коротких трубопроводов, как правило, нельзя пренебрегать кинетической энергией потока в выходном сечении трубы. Если жидкость вытекает из трубы в атмосферу, то кинетическая энергия учитывается в балансе энергии как скоростной напор, если жидкость вытекает из трубы под уровень жидкости в водоеме, то кинетическая энергия в выходном сечении «теряется» и входит в сумму местных потерь.

.

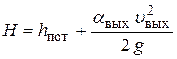(6.10)

Короткий трубопровод может иметь участки с разными диаметрами, и полная величина потерь энергии по длине представляет в этом случае сумму потерь на отдельных участках.

Рассмотрим трубопровод без разветвлений, состоящий из n участков различного диаметра, на каждом из которых имеется некоторое количество местных сопротивлений. Для определения потерь напора, как по длине, так и местных, используем формулу Вейсбаха (5.1). При этом следует помнить, что потери на трение по длине и потери на местных сопротивлениях рассчитываются по скоростям движения жидкости на тех участках трубопровода, на которых эти сопротивления возникают. Тогда, суммируя потери напора на рассматриваемом трубопроводе, запишем

.

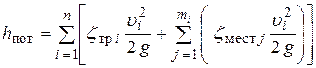(6.11)

где n – число участков трубопровода;

m_i – количество местных сопротивлений на i -ом участке трубопровода;

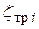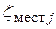и – соответствующие коэффициенты сопротивления.

Обратим внимание на то обстоятельство, что при отсутствии утечек и отбора жидкости из трубопровода, а именно такой случай и рассматривается, расход жидкости на всех участках будет одинаковым, т. е.

.

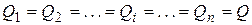С другой стороны

,

.

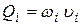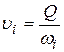Для проведения расчетов удобно с использованием этой формулы выразить скорости на участках трубопровода через скорость на каком-то одном участке. Обычно все скорости выражаются через скорость на последнем (выходном) участке. Такой участок называют «приведенным». Скорость на любом участке трубопровода можно выразить через скорость 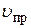и площадь 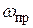на приведенном участке:

.

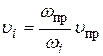Тогда можно записать

.

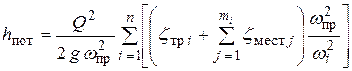(6.12)

Подставляем выражение (6.12) в формулу (6.10):

.

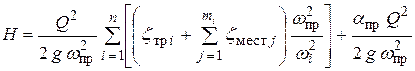Отсюда

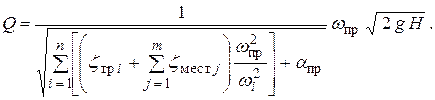
Обозначим

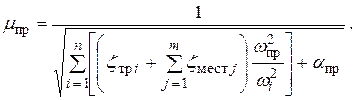
Коэффициент 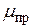называется приведенным коэффициентом расхода, отнесенным к некоторому (в нашем случае – к выходному) участку трубопровода. Тогда окончательно получаем

.

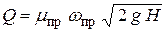(6.13)

С помощью этой формулы можно решить любую из трех основных типов задач гидравлического расчета трубопровода.

В качестве примера рассмотрим трубопровод, состоящий из двух участков труб, диаметром d ₁ и d ₂ и соответствующих длин l ₁ и l ₂. На конце второго участка установлен короткий конический насадок, имеющий выходное отверстие диаметром d ₃. Трубопровод подключен к резервуару, в котором поддерживается постоянный уровень жидкости (рис. 6.3).

Запишем уравнение Бернулли для двух сечений:

· сечение 0–0, проходящее по поверхности уровня в резервуаре;

· выходное сечение насадка 3 – 3.

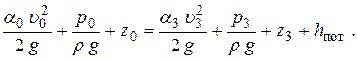
Так как уровень жидкости в резервуаре постоянен (H = const), то 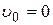, кроме того, резервуар открыт, т. е. p ₀ = p _атм, истечение происходит в атмосферу, значит, p ₃ = p _атм.

Тогда

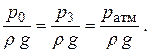
Если в качестве плоскости сравнения взять ось трубопровода, то z ₀ = H, z ₃ = 0. В итоге получаем

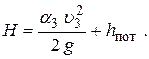
(6.14)

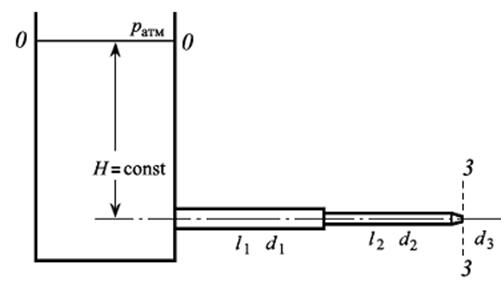
Рис. 6.3

Оценим потери напора. Они будут складываться из потерь напора на трение на первом и втором участках и потерь на местных сопротивлениях. Местными сопротивлениями в нашем примере будут

· вход в трубу из резервуара,

· внезапное сужение трубопровода на стыке первого и второго участков,

· конический насадок.

Их коэффициенты сопротивления обозначим соответственно , , .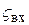

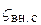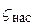Перепишем уравнение (6.14), раскрывая h _пот:

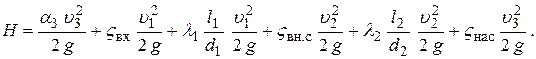
Так как расход жидкости постоянен, то

.

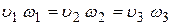Выразим скорости на участках трубопровода через скорость на выходе :

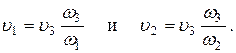
Тогда

Выражение в квадратных скобках (помимо коэффициента α ₃) можно рассматривать как суммарный коэффициент сопротивления трубопровода, приведенный к выходному сечению 3 – 3. Он называется приведенным коэффициентом сопротивления .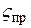

Итак, получаем

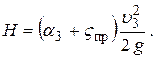
Отсюда выражаем скорость

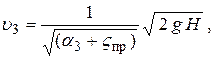
и, следовательно, расход

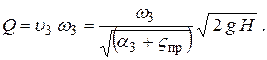
Выражение 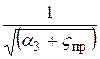обозначается через 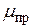, это и есть приведенный коэффициент расхода. Тогда, окончательно имеем:

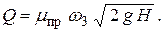
(6.15)

Можно в приведенном коэффициенте расхода выразить (привести) параметры через другую скорость (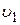 или 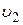). Тогда в формулу (6.15) войдет та площадь, к которой приводится коэффициент расхода.

Дата добавления: 2015-07-11