Расчет простого трубопровода

Движение жидкости в трубопроводе определяется разностью двух напоров: напора перед входом в трубопровод и напора на выходе из него. Однако если плоскость сравнения совместить со свободной поверхностью жидкости в пьезометре, присоединенном к выходному сечению, то удельная потенциальная энергия выходного сечения по отношению к плоскости сравнения будет равна нулю. В большинстве практических задач кинетическая энергия в выходном сечении либо очень мала, либо не представляет интереса для расчета. Таким образом, основная величина, определяющая движение жидкости в трубопроводе, – напор в начальном сечении относительно уровня жидкости в пьезометре, присоединенном к выходному сечению. Этот напор и называется расчетным напором трубопровода.

Величину расчетного напора можно оценить следующим образом. В общем виде разность энергий входного и выходного сечений

.

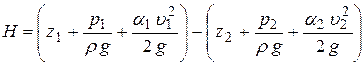Обычно жидкость входит в трубопровод из бака или водоема настолько больших размеров, что скорость перед входом можно считать пренебрежимо малой, . Кинетической энергией на выходе, как уже отмечено, также можно пренебречь. Кроме того, если оба сечения сообщаются с атмосферой (как обычно и бывает), то . Тогда

,

т. е. в этом простом случае расчетный напор есть разность геометрических высот центров тяжести входного и выходного сечений трубопровода.

Рассмотрим для начала схему расчета простого трубопровода, т. е. трубопровода, не имеющего ответвлений. Таким трубопроводом можно подавать воду из одного напорного бака в другой либо из канала (водоема) к пункту, где вода из водопровода вытекает непосредственно в атмосферу.

Труба длиной l и диаметром d может быть горизонтальной или наклонной, по ней протекает расход Q (рис. 6.1).

Рис. 6.1

Составим уравнение Бернулли для двух сечений: одно из них 1 – 1 совпадает со свободной поверхностью воды в баке, другое 2 – 2 проведено через выходное отверстие трубопровода. Плоскость сравнения 0–0проведем через центр выходного сечения трубы. Уравнение Бернулли запишется как

.

Плоскость сравнения проведена через центр выходного сечения, т. е. z ₁ = H, z ₂ = 0. Давление в обоих сечениях равно атмосферному: . Уровень жидкости в баке остается постоянным, поэтому .

Для длинных трубопроводов кинетическая энергия жидкости в выходном сечении всегда очень мала по сравнению с величиной потерь, ею можно пренебречь также, как пренебрегаем местными потерями. С учетом всего этого из уравнения Бернулли получаем

.

(6.1)

Это соотношение означает, что практически весь имеющийся напор затрачивается на преодоление сопротивления трения по длине трубопровода. Чтобы узнать потребную величину напора, следует вычислить потери энергии по длине трубопровода. На этом положении и основывается расчет длинных трубопроводов.

Потери, распределенные по длине трубопровода, можно рассчитать по формуле (5.2) – формуле Вейсбаха–Дарси:

.

Скорость движения жидкости по трубопроводу при полностью развитом турбулентном режиме течения, т. е. в случае квадратичного сопротивления, определяется формулой (4.7) – формулой Шези:

.

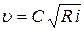Тогда расход жидкости определится как

.

Комплекс выражает величину расхода жидкости, который может пропустить рассматриваемая труба при гидравлическом уклоне, равном единице. Эту величину называют модулем расхода трубы. Вспоминая выражение для гидравлического уклона i при установившемся течении

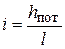
и используя обозначение модуля расхода, можем получить формулу, связывающую потери энергии и расход жидкости:

.

(6.2)

Модуль расхода трубы связан с ее диаметром и степенью шероховатости. Используя формулу Маннинга (4.9) для коэффициента C, и с учетом значения гидравлического радиуса для круглых труб 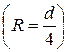, можем записать

.

Для выпускаемых промышленностью труб стандартных диаметров (сортамента) значения модуля расхода K рассчитаны и сведены в гидравлические справочники.

Таким образом, основные формулы для всех трех типов задач, возникающих при расчетах простого трубопровода, могут быть получены из формулы (6.2) с учетом формулы (6.1), т. е. использования в качестве расчетного напора величины потерь энергии:

	,	(6.3)
	,	(6.4)
	.	(6.5)

Порядок расчетов для задач первого типа (определения потребного напора) следующий.

1. По известному диаметру трубы рассчитываются площадь поперечного сечения и средняя скорость течения

.

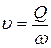2. Вычисляется число Рейнольдса

.

3. В соответствии с материалом и состоянием (новый или бывший в эксплуатации) трубопровода по гидравлическим таблицам определяется его шероховатость.

4. По рассчитанным числу Re и шероховатости из графиков Никурадзе определяется, какой случай сопротивления по длине имеет место. Это позволит выбрать вид формулы для расчета коэффициента C.

5. Рассчитывается или из гидравлических таблиц определяется значение модуля расхода K.

6. При известных Q, l и K по формуле (6.3) находится величина напора. Зачастую найденную таким образом величину H несколько увеличивают (на 2–5 %) для запаса на неучтенные местные потери.

В задачах второго типа (определение расхода) изначально нельзя вычислить скорости, рассчитать число Рейнольдса и определить закон сопротивления по длине трубы. В задачах третьего типа (расчет необходимых диаметров) неизвестны также изначальные характеристики шероховатости трубопровода. Такие задачи решаются путем последовательных приближений, при котором предварительные расчеты проводят, задаваясь некоторыми начальными значениями неизвестных параметров. После получения результата производится коррекция начальных предположений, и расчеты повторяются. При использовании возможностей современной вычислительной техники эти методы не вызывают принципиальных трудностей.

Если же рассматриваются трубопроводы с заведомо большой скоростью течения и значительной шероховатостью, то это позволяет уверенно предположить наличие квадратичного закона сопротивления. Тогда, применяя формулы Шези, Павловского или Маннинга, можно решать такие задачи без подбора.

Дата добавления: 2015-07-11