Основные теоретические положения

Уравнение Д.Бернулли для реального потока жидкости для двух произвольно взятых сечений имеет следующий вид:

, (9)

где: z₁, z₂ – нивелирная высота соответственно для первого и второго сечений, м;

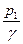и – пьезометрическая высота соответственно для первого и второго сечений, м;

и – коэффициент кинетической энергии потока (или коэффициент Кориолиса), учитывающий неравномерность распределения скоростей по сечению потока (величина безразмерная);

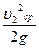и – скоростная высота или скоростной напор, м;

– сумма всех гидравлических потерь на участке между первым и вторым сечение, м.

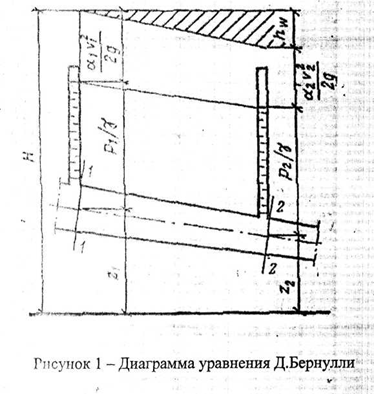
Итак, с геометрической точки зрения уравнение Д.Бернулли показывает, что сумма трех высот – геометрической, пьезометрической и скоростной с учетом всех гидравлических потерь – есть величина, постоянная вдоль струйки.

С энергетической точки зрения члены уравнения Д.Бернулли имеют следующий смысл:

z – удельная энергия положения; -.

z+p/y — удельная потенциальная энергия жидкости;

v /2g кудельная кинетическая энергия.,

Таким образом, – уравнение Д.Бернулли является примером закона сохранения энергии М.В.Ломоносова в применении к жидкости.

Дата добавления: 2015-07-11