Нагрев проводников.

Если через проводник, имеющий температуру окружающей среды, проходит ток, то температура проводника постепенно повышается, т.к. вся энергия потерь переходит в тепло.[1]

Количество тепла, выделенного в проводнике в течение времени dt, будет составлять

где I – действующее значение тока, проходящего по проводнику А;

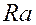- активное сопротивление проводника при переменном токе, Ом;

Р – мощность потерь, переходящих в тепло, Вт.

Энергия, идущая на нагрев проводника, равна

где - вес токоведущего проводника, кг,

С - удельная теплоемкость материала проводника,

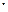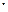Вт с/кг град;

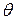- превышение температуры проводника над окружающей средой.

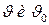- температуры проводника и окружающей среды, .

Энергия, отводимая с поверхности проводника в течение времени dt за счет теплоотдачи, пропорциональна превышению температуры проводника над температурой окружающей среды:

где К – общий коэффициент, усиливающий все виды теплоотдачи, Вт/ ;

F – Поверхность охлаждения проводника, .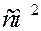

Уравнение теплового баланса за время неустановившегося теплового процесса можно записать в следующем виде:

Для нормального режима, когда температура изменяется в небольших пределах, можно принять, что R, C и K – постоянные величины. Кроме того до включения тока проводник имел температуру окружающей среды т.е. при t=0 .

Решением этого дифференциального уравнения нагрева проводника будет:

; (1)

где А – постоянная интегрированная, зависящая от начатых условий при t=0 , тогда для t=0 получаем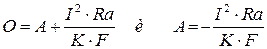

Подставляя значения постоянной интегрирования А в формулу (1), получаем:

(2)

Из этого уравнения следует, что нагрев токоведущего проводника происходит по экспоненциальной кривой.

Рис.1.

С изменением времени подъем температуры проводника замедляется и температура достигает установившегося значения.

Это уравнение дает температуру проводника в любой момент времени t сначала прохождения тока.

Величина установившегося перегрева может быть получена, если в управлении нагрева принять :

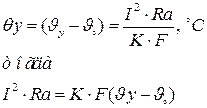
Отсюда видно, что все выделяющееся в проводнике тепло будет отдаваться в окружающее пространство.

Введя в основное уравнение нагрева (2) 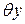и обозначив , получим то же уравнение в более простом виде:

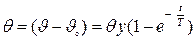
Величина называется постоянной времени нагрева и представляет собой отношение теплопоглощающей способности тела к его теплоотдающей способности.

Она зависит от размеров, поверхности, свойств проводника или тела и не зависит от времени и температуры.

Эта величина характеризует время достижения установившегося режима нагрева и принимается за масштаб измерения времени на диаграммах нагрева.

На практике время достижения установившейся температуры принимают равным (3-4) Т, т.к. при этом температура нагрева превышает 98% своего окончательного значения. Постоянную времени нагрева для простых токоведущих конструкций легко вычислить, а для аппаратов и машин она определяется путем тепловых испытаний и последующих графических построений. Графически постоянная времени нагрева определяется как подкасательная ОТ, построенная по кривой нагрева. А сама касательная ОВ к кривой характеризует подъем температуры проводника при отсутствии теплоотдачи. В том случае, когда в начальный момент до включения тока проводник уже был нагрет и имел превышение температура над температурой окружающей среды , дифференциальное уравнение нагрева следует решать при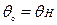

Тогда

Если предположить, что процесс нагрева проводника происходит без отдачи тепла, то уравнение нагрева примет вид:

т.е температура перегрева будет нарастать по линейному закону пропорционального времени.

Величина постоянной времени колеблется от нескольких минут у шин до нескольких часов у трансформаторов и генераторов.

Т для электродвигателей мощностью 100-200 кВт – 2-3 часа.

Т для трансформаторов 2-4 часа.

Т для турбогенераторов 12-20 часов.

Мощные генераторы нагреваются очень медленно и установившаяся температура их достигается через несколько суток.

При отключении тока прекращается подвод энергии к проводнику, т.е. , проводник будет охлаждаться. Основное уравнение нагрева для этого случая следующее:

Отсюда

если охлаждение начинается с установившейся температуры, то оно принимает вид:

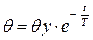
Кривая охлаждения есть та же кривая нагрева, но обращенная выпуклостью вниз (к оси абсцисс).

Рис. 2

Постоянная времени нагрева может быть определена по кривой охлаждения как подкасательная для любой точки кривой.

Дата добавления: 2015-07-11