Определение параметров линейной регрессии в зависимости от ошибок и скорости выполнения заданий теста

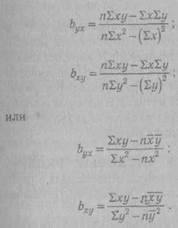
К примеру, даны два ряда оценок ус­пешности выполнения теста. Пусть X — скорость выполнения; У — количество ошибок. Расчет уравнения регрессии в данном случае приведен в табл. 22.

Подставив полученные при расчете в таблицу значения, получаем уравнение регрессии:

у= 1,78 + 0,52*.

Проверка расчетэв может быть осуще­ствлена путем сопоставления эмпиричес­ких и теоретических значений {у_{ и y_t),

которые должны быть близкими по вели­чинам.

Квадрат коэффициента корреляции (в примере г = 0,86, г² = 0,75) показываем что 75% общей дисперсии У объясняют­ся влиянием переменной X, остальные 25% обусловлены влиянием неучтенных в уравнении факторов.

При оценке зависимости результирую­щего признака от нескольких факторов строится уравнение множественной рег­рессии. Интерпретация коэффициентов регрессии аналогична случаю парной рег­рессии.

Коэффициент регрессии находится в тесной связи с коэффициентами корреля­ции (см. Корреляционный анализ). Коэф­фициент корреляции представляет собою среднее геометрическое из коэффициен­тов регрессии признаков:

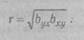
Благодаря этому имеется возможность определения неизвестной величины по значениям коэффициентов регрессии и контроля правильности расчета коэффи­циента корреляции.

Стандартная ошибка выборочного ко­эффициента регрессии может быть рас­считана при помощи следующих уравне­ний:

Достоверность выборочного коэффи­циента регрессии проверяется с помощью критерия Стьюдента с k = п - 2 числом степеней свободы и принятым уровнем значимости (а). Нулевая гипотеза (см. Оценка типа распределения) сводится к предположению, что в генеральной сово­купности коэффициент регрессии равен нулю.

Различные способы Р. а. широко при­меняются в эмпирических психодиагнос­тических исследованиях для выявления влияния отдельных факторов на результи­рующие показатели теста, анализа на­дежности, внутренней и внешней валид-ности методики и др.

РЕПРЕЗЕНТАТИВНОСТЬ (франц. ге-presentatif — показательный) свойство выборочной совокупности представлять характеристики генеральной совокупно­сти. Р. означает, что с некоторой наперед заданной или определенной статистичес­ки погрешностью можно считать, что представленное в выборочной совокупно­сти распределение изучаемых признаков соответствует их реальному распределе­нию.

Для обеспечения Р. выборки данных необходимо учесть ряд обязательных для

любого исследования условий. Среди них важнейшими являются следующие: а) каждая единица генеральной совокуп­ности должна иметь равную вероятность попадания в выборку; б) выборка пере­менных производится независимо от изу­чаемого признака; в) отбор производится из однородных совокупностей; г) число единиц в выборке должно быть достаточ­но большим; д) выборка и генеральная совокупность должны быть по возможно­сти статистически однородны (х_(выб)-- ^(_ген)->0), показатели вариации при увеличении числа наблюдений сближа­ются между собой:

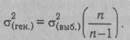
Статистическое определение Р. в практической психодиагностике необхо­димо для установления Р. норм психомет­рического теста, а также обоснованности выборок, на которых проводится стан­дартизация методик. В широком понима­нии Р. связана с комплексом характерис­тик валидности методики.

РЖИЧАНА ЧИСЛОВЫЕ РЯДЫ —

тест интеллекта, относящийся к груп­пе невербальных. Разработан П. Ржича-ном в 1973 г.

Испытуемому необходимо выявить принципы, лежащие в основе предлага­емых ему последовательностей. Автор включил в тест задачи, содержащие как восходящие, так и нисходящие арифмети­ческие и геометрические последователь­ности, простые и комбинированные, с че­редованием различных арифметических операций. Каждое задание представляет собой ряд из 4-8 чисел. Испытуемый дол­жен закончить его двумя числами, напр.:

1) 3,6,9,12,15,_______;

2) 29,25,21,17,___,___;

3) 5,3,6,4,7,5,8,___,___

Задания размещены в порядке возрас­тающей трудности. На первой странице тестовой тетради приводятся примеры правильных решений. Время выполнения ограничено, о чем сообщается испытуе­мым. За каждый правильный ответ при­суждается 1 балл. Сумма баллов может быть переведена с помощью таблиц в оценки шкальные в виде стэнов. Имеют­ся две параллельные формы теста А и В. Факторный анализ выявил высокий удельный вес фактора G. Результаты те­ста улучшаются с возрастом. В целом тест эффективен для обследования детей школьного возраста, обладает высокой дискриминативностью для популяции лиц со средним уровнем интеллектуального развития. Коэффициент внутренней со­гласованности составляет 0,88. Валид-ность критериальная определялась от­носительно успеваемости в школе. Наи­более высокие показатели связи были об­наружены между результатами Р. ч. р. и успеваемостью по математике (г = 0,54). Для мальчиков этот коэффициент соста­вил г = 0,63, для девочек — г = 0,59. Эти данные касаются формы В. Валидность формы А оказалась несколько ниже, кор­реляции с оценкой по математике была г-0,46. Возможно недостаточное соот­ветствие форм Аи В друг другу. Тест по­ложительно коррелирует с интеллекту­ального потенциала тестом. Р. ч. р. аналогичны субтесту ZR Амтхауэра ин­теллекта структуры теста.

Р. ч. р. нашли применение в отечест­венной психодиагностике. Методика ре­комендуется как средство оценки уровня общих способностей в комплексе с други­ми тестами. Наиболее широко использу­ются в профконсультации и профотборе.

РИСОВАНИЯ ОБРАЗЦОВ ТЕСТ —

тест специальных способностей. Пред­назначен для диагностики пространст­венного воображения и психомоторной

активности. Разработан Й. X. Райскуром в 1947 г.

Содержание работы испытуемого со­стоит в соединении точек внутри квадра­та так, чтобы возник образец, изображен­ный рядом с квадратом (рис. 57).

Рис. 57. Стимульный материал Рисования образ­цов теста

Количество точек в рабочем квадра­те— 49. Тестовая тетрадь состоит из двух частей: левой и правой. Каждое зада­ние выполняется поочередно обеими ру­ками. За точное копирование образца на­числяется 1 балл. Оценка первичная пе­реводится в z-показатели или процентили (см. Оценки шкальные. Стандартные по­казатели рассчитаны для правой и левой рук. По таблицам определяется и общий стандартный показатель. Нормы разрабо­таны для выпускников школ (возраст 15-17 лет).

При анализе валидности конструк-тной выявлена некоторая связь результа­тов Р. о. т. с тестом Проверка G (г = 0,187 для правой руки, г = 0,095 для левой ру­ки, и с тестом Вонкомера (г = 0,546 и г = 0,502 соответственно). Валидность критериальная анализировалась путем

сопоставления результатов Р. о. т. с груп­повой экспертной оценкой моторной лов­кости испытуемых (г = 0,678).

Р. о. т. является моделью исследова­ния психомоторного развития детей и под­ростков. По мнению Й. Вонкомера (1969), он с успехом применяется в консульта­тивной и профориентационной работе. Используется и в клинической психодиаг­ностике (исследование особенностей ви­зуальной памяти, латерализации функций и т. д.).

Данных об использовании в СНГ нет.

«РИСУНКА СЕМЬИ» МЕТОДИКИ

(Drawing-Family Techniques) — группа проективных методик для оценки внут­рисемейных отношений. Основана на ана­лизе и интерпретации рисунков. «Р. с.» м., как правило, применяются при обследова­нии детей,

Рисуночные методики являются одни­ми из наиболее распространенных среди проективных тестов (см. «Нарисуй чело­века» тест, «Дом—дерево—человек» тест и др.). Идея использовать технику рисунка для диагностики внутрисемейных отношений возникла у целого ряда иссле­дователей. Подробная схема проведения обследования и интерпретации результа­тов впервые была разработана для теста «Нарисуй свою семью» (В. Вульф, 1947). Опыт применения рисуночной методики в этих целях был описан в работах В. Хьюл-са (1951-1952 гг.). Согласно схеме ин­терпретации по В. Вульфу, в рисунке анализируются: а) последовательность рисования членов семьи, их простран­ственное расположение, наличие пропус­ков отдельных членов семьи; б) отличия в формах и пропорциях отдельных фигур. Согласно В. Вульфу, последовательность рисозания указывает на значимость дан­ного члена семьи. Пропуск члена семьи часто выражает стремление избавиться от эмоционально-неприемлемого лица.

Если величина изображенных фигур не соответствует реальной иерархии, то та­кое восприятие относят за счет степени субъективной доминантности и значимо­сти. В. Вульф обращал внимание также на интерпретацию различий в рисовании от­дельных частей тела, исходя из возмож­ности переживаний, связанных с их фун­кциями.

В работах В. Хьюлса были предложе­ны интерпретационные схемы «Р. с.» м., базирующиеся на самом процессе рисова­ния (использование цветов, вычеркива­ния, стирания, сомнения, сопутствующие эмоциональные проявления, коммента­рии).

Дальнейшее развитие «Р. с.» м. полу­чили в работах Л. Кормана(1964),Р. Бер-нса и С. Кауфмана (1972). В инструкции к методике Л. Кормана предусмотрено за­дание нарисовать не «семью» или «свою семью», как в методике В. Вульфа и В. Хьюлса, а «семью, как ты ее себе пред­ставляешь». Благодаря такой установке имеется возможность использовать менее структурированный объект (стимул) (см. Проективные методики). При интерпре­тации результата авторы обращают вни­мание на случаи, когда испытуемый рису­ет большую или меньшую семью, чем она является на самом деле (авторы считают, что это указывает на функционирование определенных защитных механизмов; чем больше несовпадение, тем больше неудов­летворенность существующей ситуаци­ей). В рисунках, по Л. Корману, анали­зируют: а) его графическое качество (ха­рактер линий, пропорции фигур, аккурат­ность, использование, пространства);

б) формальную структуру (динамичность рисунка, расположение членов семьи);

в) содержание (анализ смысла рисунка). Параллельно с традиционным проведени­ем обследования (чтение и выполнение задания) предлагаются специальные воп­росы, подталкивающие испытуемого к об-

суждению темы отношении в семье (напр.: «Кто в семье самый плохой?»), предусматривающие прямой положитель­ный или отрицательный выбор (напр.: «Отец задумал поездку в автомобиле, но в нем не хватает места для всех. Кто оста­нется дома?»), а также вопросы, уточня­ющие смысл нарисованной ситуации для ребенка.

Вариантом «Р. с.» м., получившим наи­большую известность в зарубежной пси­ходиагностике, является «Кинетический рисунок семьи», предложенный Р. Берн-сом и С. Кауфманом. В нем нужно нари­совать каждого из членов семьи в дей­ствии. Интерпретация материала основа­на на символическом толковании изобра­женных отношений, действий, предметов; при этом часть трактовок, предложенных авторами методики, основана на принци­пах психоанализа.

Техника «рисунка семьи» в советской психодиагностике нашла применение в клинических исследованиях. А. И. Заха­ровым (1977) предложен вариант методи­ки, состоящий из двух заданий. Для вы­полнения первого из них ребенку нужно нарисовать в четырех «комнатах», распо­ложенных на двух «этажах», по одному из членов семьи, включая себя. При интер­претации рисунка обращается внимание на размещение членов семьи по этажам и на то, кто из них находится рядом с ребен­ком (т. е. является эмоционально наибо­лее близким). Второе задание — выпол­нение рисунка в свободной форме без каких-либо дополнительных инструкций. Вариант «Р. с.» м. со сложной и диф­ференцированной интерпретационной схемой предложен Г. Т. Хоментаускасом в 1985 г.

Дата добавления: 2015-07-10