|
Читайте также: |
Уравнения изгибающих моментов по участкам в горизонтальной плоскости (рис. 6.11).
Участок d (0£ x £ d): 
,
при x= 0: 
; при x=d: 
.
Участок e (0£ x £ e): 
,
при x= 0: 
; при x=e: 
.
Участок c (0£ x £ f): 
,
при x= 0: 
; при x=f: 
.
Уравнения изгибающих моментов по участкам в вертикальной плоскости.
Участок d (0£ x £ d): 
.
при x= 0: 
; при x=d: 
.
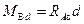Участок e (0£ x £ e): 
,
при x= 0: 
; при x=e: 
.
Участок f (0£ x £ f): 
,
при x= 0: 
;
при x=f: 
.
Значения суммарного изгибающего момента определяются по формуле: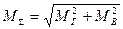 
.
Проверку проводят в тех сечениях, где суммарный изгибающий момент принимает наибольшие значения.
Определяем для опасного сечения коэффициенты запаса выносливости по нормальным 
и касательным 
напряжениям:
 ,
| (6.10) |
 ,
|
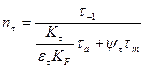где 
и 
- пределы выносливости материала вала при симметричном цикле напряжения изгиба и кручения соответственно, МПа;
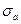и 
- амплитуды циклов изменения нормальных и касательных напряжений, МПа;
и 
- средние значения циклов изменения нормальных и касательных напряжений, МПа;
и 
- эффективные коэффициенты концентрации напряжений при изгибе и кручении соответственно (табл. 6.16);
и 
- коэффициенты, учитывающие масштабный фактор (табл. 6.17);
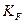- коэффициент, учитывающий влияние качества поверхности (табл. 6.18);
и 
- коэффициенты, учитывающие влияние асимметрии цикла напряжений на прочность вала при изгибе и кручении соответственно (табл. 6.19).
Нормальные напряжения в поперечных сечениях вала изменяются по симметричному циклу, тогда среднее напряжение 
, а амплитуда напряжений 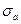равна расчетным напряжениям изгиба 
:
 ,
| (6.11) |
где 
- осевой момент сопротивления сечения (табл. 6.15).
Касательные напряжения в поперечных сечениях вала изменяются, обычно, по пульсирующему (отнулевому) циклу, в этом случае значения амплитуды и средней величины касательного напряжения в цикле можно определить по формуле:
 ,
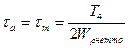| (6.12) |
где 
- полярный момент сопротивления сечения (табл. 6.15).
Общий коэффициент запаса выносливости:
 .
| (6.13) |
Таблица 6.15
Дата добавления: 2015-07-10; просмотров: 162 | Нарушение авторских прав