Расчет конической передачи

Исходные данные:

Крутящий момент на валу конического колеса Т₃ = 35924 Н×мм.

Число оборотов промежуточного вала редуктора n₃ = 464 об/мин.

Передаточное число конической передачи u_к = 3,15.

Срок службы привода L_h = 29784 часов.

Выбор материалов для изготовления конической зубчатой передачи:

- шестерня – сталь 45, термообработка - улучшение до твёрдости 235…260 НВ;

- колесо – сталь 45, термообработка - нормализация до твёрдости 180…205 НВ.

Допускаемые контактные напряжения определяем по материалу колеса, как менее твёрдого.

,

где МПа, предел выносливости материала по контактным напряжениям при отнулевом цикле нагружения;

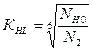- коэффициент долговечности при расчёте по контактным напряже­ниям;

N₀ = 10⁷ – базовое число циклов нагружения;

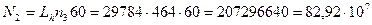- расчётное число циклов нагружения зубьев колеса. Так как N₂ >N_Н0, то принимаем К_HL = 1;

S_H = 1,1 – коэффициент безопасности.

МПа.

Допускаемые напряжения изгиба:

,

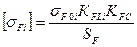где σ_F01, σ_F02 – предел выносливости материала по напряжениям изгиба при отнулевом цикле нагружения для шестерни и колеса, соответственно;

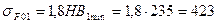МПа;

МПа.

- коэффициент долговечности при расчёте по напряжениям изгиба.

N_F0 = 5∙10⁶ – базовое число циклов, т.к. N₂> N_F0, то .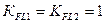

S_F = 1,75 – коэффициент безопасности.

МПа,

МПа.

Определение внешнего делительного диаметра колеса d_e, мм:

,

где K_Hb –коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, с прирабатывающимися прямыми зубьями K_Hb= 1; u_Z – коэффициент, учитывающий вид зубьев конических колёс, для прямозубых колёс u_Z=1.

мм.

Принимаем мм.

Определяем углы делительных конусов шестерни d₁ и колеса d₂:

,

.

Определяем внешнее конусное расстояния R_e, мм:

.

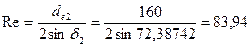Определение ширины зубчатого венца b, мм:

,

где y_R = 0,285 – коэффициент ширины зубчатого венца.

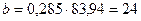мм.

Определяем внешний окружной модуль зацепления, мм:

.

Назначаем m_е=2,5 мм.

Определяем числа зубьев.

Число зубьев колеса: .

Число зубьев шестерни: .

Фактическое передаточное число:

.

Отклонение фактического передаточного числа от номинальной величины:

.

Определяем действительные углы делительных конусов шестерни d₁ и колеса d₂:

,

.

Геометрические параметры зацепления, мм:

делительный диаметр шестерни ;

диаметры окружностей выступов:

шестерни ,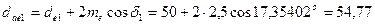

колеса ;

диаметры окружностей впадин:

шестерни ,

колеса .

Определим средний окружной модуль, мм:

.

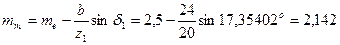Определяем средние делительные диаметры шестерни d_m1 и колеса d_m2, мм:

,

.

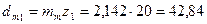Проверочный расчёт

Определяем окружную скорость, м/c:

.

По окружной скорости назначаем 8-ю степень точности передачи.

Определяем коэффициенты расчётной нагрузки.

Коэффициенты K_Fa и K_Ha, учитывающие распределение нагрузки между зубьями, для прямозубой передачи принимаем: K_Fa=K_Ha= 1.

По степени точности и окружной скорости по таблице 3.6 определяем коэффициенты динамической нагрузки при расчете по контактным напряжениям K_Hv= 1,128 и напряжениям изгиба K_Fv= 1,308.

Коэффициенты K_Fb и K_Hb, учитывающие неравномерность распределения нагрузки по длине зуба, для прямозубой передачи принимаем: K_Hb=K_Fb = 1.

,

= 1,308.

Окружная сила, действующая в зацеплении, Н:

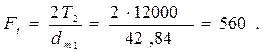
Проверка по контактным напряжениям s_H, МПа:

.

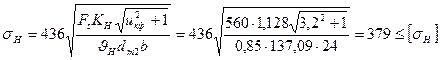Определяем эквивалентные числа зубьев шестерни и колеса:

,

.

Коэффициент формы зуба шестерни Y_F1= 4,07и колеса - Y_F2= 3,63.

Проверка прочности зубьев колеса и зубьев шестерни по напряжениям изгиба. Условия прочности:

,

,

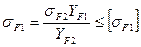где Y_b= 1 - коэффициент, учитывающий наклон зубьев; u_F – коэффициент, учитывающий вид зубьев конических колёс, для прямозубых колёс u_F= 0,85.

,

.

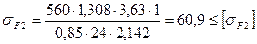Прочность зубьев по напряжениям изгиба обеспечена.

---

Дата добавления: 2015-07-10