Прямоугольный поршень

Пусть антенна в виде непрерывного параллелограмма расположена в плоскости xOy/

XН антенны в виде параллелограмма в жестком экране при равномерном амплитудом распределении и компенсации в направлении может быть записана таким образом:

(1)

Здесь введены обозначения

В случае антенны в виде прямоугольника 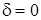. Выражение (1) преобразуется к виду

* *

Выражение (2) определяет пространственную XН антенны в виде прямоугольного поршня. Заметим, что первый сомножитель представляет собой XН отрезка длиной a, а второй b.

В зависимости от плоскости, в которой ведётся рассмотрение, выражение (2) будет видоизменяться соответственно значениям углов и .

Основные свойства и XН антенны в виде отрезка.

1) функция sint/t обращается в при всех 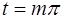, где m - целое 0.

- условия нулей,

- угол нуля XH.

2)

3) добавочные max монотонно убывают по закону ; имеют величины .;

0,22;0,13;0,09;0,07;0,06.

Располагаются добавочные max ~ посередине между соседними крайними.

Боковой лепесток не может быть меньше 22% в отсутствие амплитудного распределения. Величина дополнительных max не зависит от волновых размеров.

4) при 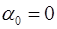, т.е. в отсутствие компенсации, число нулей в первом квадрате (0-90⁰) равно целой части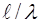

5) ; .

.

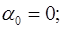
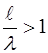КОК

В общем случае

.

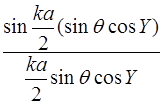Зависит от

Имеет max в направл. , т.к.. в этом направлении давления от всех элементов дуги складывается синфазно.

Круглый поршень (антенна в виде круга, плотно заполненного элементами)

Ось oz перпендикулярна плоскости антенны. x,y,z; – прямоугольная система координат;

- в сферической системе координат.

- радиус- вектор точечного источника

R – радиус круга

М- точка наблюдения (в дальней зоне)

Будем искать давление, развиваемое антенной в направлении ox, (поскольку симметрично) т.е.

(7)

Q – производительность источника;

S- площадь антенны;

-колебательная скорость.

Переходя к полярным координатам , .

.

- табличное значение функции Бесселя нулевого порядка.

(8)

формула для функции Бесселя n-ого порядка

В интеграле (8) проведём замену переменных.

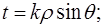
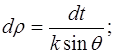n=0.

Для пределов интегрирования

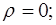
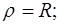
Особенности XH.

1) Направление максимумов по оси oz

при .

Дополнительные max после первого нуля равны

отсюда следует, что уровень первого бокового лепестка XH не может быть меньше 13 % в случае поршневой круглой антенны, если не применять специальные способы их подавления.

4) Нули XH определены при

5) Когда , ширина XH на уровне 0,7 определяется по приблизительной формуле

.

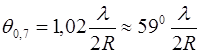6) Острота направления действия

.

7)Ширина по уравнению 0,7

.

КОК

При больших волновых размерах плоско-синфазно возбужденной непрерывной антенны при равномерной амплитуде распределения

При малых волновых размеров и наличии амплитудного и фазового распределений

Из графика видно, что функция начиная с не превосходит величины 0,06, то при ,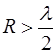

КОК рассчитанный по полной формуле, отличается от величины не более чем на 6%.

Цилиндрические антенны.

X,Y,Z- прямоугольник

- цилиндрические координаты

Высота цилиндра H диаметр D=2R

Ось О_Z совпадает с осью цилиндра.

Центр системы координат совпадает с

центром цилиндра.

Дата добавления: 2015-07-10